Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-29T00:25:58.509Z Has data issue: false hasContentIssue false
  • English
  • Français

Confined inclined thermal convection in low-Prandtl-number fluids

Published online by Cambridge University Press:  10 July 2018

Lukas Zwirner Open the ORCID record for Lukas Zwirner [Opens in a new window]  and
Olga Shishkina Open the ORCID record for Olga Shishkina [Opens in a new window]
Lukas Zwirner*
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077 Göttingen, Germany
Olga Shishkina
Affiliation:
Max Planck Institute for Dynamics and Self-Organization, Am Fassberg 17, 37077 Göttingen, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Any tilt of a Rayleigh–Bénard convection cell against gravity changes the global flow structure inside the cell, which leads to a change of the heat and momentum transport. Especially sensitive to the inclination angle is the heat transport in low-Prandtl-number fluids and confined geometries. 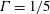The purpose of the present work is to investigate the global flow structure and its influence on the global heat transport in inclined convection in a cylindrical container of diameter-to-height aspect ratio $\unicode[STIX]{x1D6E4}=1/5$. The study is based on direct numerical simulations where two different Prandtl numbers 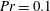$Pr=0.1$ and 1.0 are considered, while the Rayleigh number, 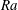$Ra$, ranges from 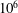$10^{6}$ to 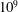$10^{9}$. For each combination of 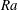$Ra$ and 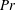$Pr$, the inclination angle is varied between 0 and 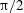$\unicode[STIX]{x03C0}/2$. An optimal inclination angle of the convection cell, which provides the maximal global heat transport, is determined. For inclined convection we observe the formation of two system-sized plume columns, a hot and a cold one, that impinge on the opposite boundary layers. These are related to a strong increase in the heat transport.

JFM classification

Convection: Convection in cavities Turbulent Flows: Turbulent convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 850 , 10 September 2018 , pp. 984 - 1008
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1995 Turbulence and internal waves in side-heated convection. Phys. Rev. E 51, 5681–5687.Google Scholar
Bodenschatz, E., Pesch, W. & Ahlers, G. 2000 Recent developments in Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 32, 709–778.Google Scholar
Castaing, B., Rusaouën, E., Salort, J. & Chillà, F. 2017 Turbulent heat transport regimes in a channel. Phys. Rev. Fluids 2, 062801.Google Scholar
Chen, Y.-M. & Pearlstein, A. J. 1989 Stability of free-convection flows of variable-viscosity fluids in vertical and inclined slots. J. Fluid Mech. 198, 513–541.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35 (7), 58.Google Scholar
Chong, K. L., Huang, S.-D., Kaczorowski, M. & Xia, K.-Q. 2015 Condensation of coherent structures in turbulent flows. Phys. Rev. Lett. 115, 264503.Google Scholar
Chong, K. L., Wagner, S., Kaczorowski, M., Shishkina, O. & Xia, K.-Q. 2018 Effect of Prandtl number on heat transport enhancement in Rayleigh–Bénard convection under geometrical confinement. Phys. Rev. Fluids 3, 013501.Google Scholar
Chong, K. L. & Xia, K.-Q. 2016 Exploring the severely confined regime in Rayleigh–Bénard convection. J. Fluid Mech. 805, R4.Google Scholar
Ciliberto, S., Cioni, S. & Laroche, C. 1996 Large-scale flow properties of turbulent thermal convection. Phys. Rev. E 54, R5901–R5904.Google Scholar
Daniels, K. E., Plapp, B. B. & Bodenschatz, E. 2000 Pattern formation in inclined layer convection. Phys. Rev. Lett. 84 (23), 5320–5323.Google Scholar
Daniels, K. E., Wiener, R. J. & Bodenschatz, E. 2003 Localized transverse bursts in inclined layer convection. Phys. Rev. Lett. 91 (11), 114501.Google Scholar
Dropkin, D. & Somerscales, E. 1965 Heat transfer by natural convection in liquids confined by two parallel plates which are inclined at various angles with respect to the horizontal. Trans. ASME J. Heat Transfer 87 (1), 77–82.Google Scholar
Frick, P., Khalilov, R., Kolesnichenko, I., Mamykin, A., Pakholkov, V., Pavlinov, A. & Rogozhkin, S. A. 2015 Turbulent convective heat transfer in a long cylinder with liquid sodium. Europhys. Lett. 109, 14002.Google Scholar
Fujimura, K. & Kelly, R. E. 1993 Mixed mode convection in an inclined slot. J. Fluid Mech. 246, 545–568.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Guo, S.-X., Zhou, S.-Q., Cen, X.-R., Qu, L., Lu, Y.-Z., Sun, L. & Shang, X.-D. 2015 The effect of cell tilting on turbulent thermal convection in a rectangular cell. J. Fluid Mech. 762, 273–287.Google Scholar
Huang, L. & El-Genk, M. S. 1994 Heat transfer of an impinging jet on a flat surface. Intl J. Heat Mass Transfer 37 (13), 1915–1923.Google Scholar
Huang, S.-D., Kaczorowski, M., Ni, R. & Xia, K.-Q. 2013 Confinement induced heat-transport enhancement in turbulent thermal convection. Phys. Rev. Lett. 111, 104501.Google Scholar
Jambunathan, K., Lai, E., Moss, M. A. & Button, B. L. 1992 A review of heat transfer data for single circular jet impingement. Intl J. Heat Fluid Flow 13 (2), 106–115.Google Scholar
Kooij, G. L., Botchev, M. A., Frederix, E. M. A., Geurts, B. J., Horn, S., Lohse, D., van der Poel, E. P., Shishkina, O., Stevens, R. J. A. M. & Verzicco, R. 2018 Comparison of computational codes for direct numerical simulations of turbulent Rayleigh–Bénard convection. Comput. Fluids 166, 1–8.Google Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2015 Vertical natural convection: application of the unifying theory of thermal convection. J. Fluid Mech. 764, 349–361.Google Scholar
Ng, C. S., Ooi, A., Lohse, D. & Chung, D. 2017 Changes in the boundary-layer structure at the edge of the ultimate regime in vertical natural convection. J. Fluid Mech. 825, 550–572.Google Scholar
Riedinger, X., Tisserand, J.-C., Seychelles, F., Castaing, B. & Chillà, F. 2013 Heat transport regimes in an inclined channel. Phys. Fluids 25 (1), 015117.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12 (8), 085014.Google Scholar
Scheel, J. D. & Schumacher, J. 2016 Global and local statistics in turbulent convection at low Prandtl numbers. J. Fluid Mech. 802, 147–173.Google Scholar
Schumacher, J., Bandaru, V., Pandey, A. & Scheel, J. D. 2016 Transitional boundary layers in low-Prandtl-number convection. Phys. Rev. Fluids 1, 084402.Google Scholar
Schumacher, J., Götzfried, P. & Scheel, J. D. 2015 Enhanced enstrophy generation for turbulent convection in low-Prandtl-number fluids. Proc. Natl Acad. Sci. USA 112 (31), 9530–9535.Google Scholar
Shishkina, O. 2016 Momentum and heat transport scalings in laminar vertical convection. Phys. Rev. E 93, 051102(R).Google Scholar
Shishkina, O. & Horn, S. 2016 Thermal convection in inclined cylindrical containers. J. Fluid Mech. 790, R3.Google Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E. S. C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114, 114302.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.Google Scholar
Shishkina, O. & Wagner, S. 2016 Prandtl-number dependence of heat transport in laminar horizontal convection. Phys. Rev. Lett. 116, 024302.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650–3653.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid Mech. 730, 295–308.Google Scholar
Sun, C., Xi, H.-D. & Xia, K.-Q. 2005 Azimuthal symmetry, flow dynamics, and heat transport in turbulent thermal convection in a cylinder with an aspect ratio of 0.5. Phys. Rev. Lett. 95, 074502.Google Scholar
Teimurazov, A. & Frick, P. 2017 Thermal convection of liquid metal in a long inclined cylinder. Phys. Rev. Fluids 2, 113501.Google Scholar
Vasilev, A. Yu., Kolesnichenko, I. V., Mamykin, A. D., Frick, P. G., Khalilov, R. I., Rogozhkin, S. A. & Pakholkov, V. V. 2015 Turbulent convective heat transfer in an inclined tube filled with sodium. Tech. Phys. 60, 1063–7842.Google Scholar
Verzicco, R. & Camussi, R. 1997 Transitional regimes of low-Prandtl thermal convection in a cylindrical cell. Phys. Fluids 9 (5), 1287–1295.Google Scholar
Wagner, S. & Shishkina, O. 2013 Aspect ratio dependency of Rayleigh–Bénard convection in box-shaped containers. Phys. Fluids 25, 085110.Google Scholar
Weiss, S. & Ahlers, G. 2013 Effect of tilting on turbulent convection: cylindrical samples with aspect ratio 𝛾 = 0. 50. J. Fluid Mech. 715, 314–334.Google Scholar
Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transitions in turbulent thermal convection. Phys. Fluids 20, 055104.Google Scholar

Zwirner and Shishkina supplementary movie 1

Isosurfaces of the temperature for Pr=1, Ra=10^8 and β/π=0.

Download Zwirner and Shishkina supplementary movie 1(Video)
Video 2.8 MB

Zwirner and Shishkina supplementary movie 2

Isosurfaces of the temperature and streamlines for Pr=1, Ra=10^8 and β/π=0.15.

Download Zwirner and Shishkina supplementary movie 2(Video)
Video 36 MB