Article contents
Condensates in rotating turbulent flows
Published online by Cambridge University Press: 23 February 2018
Abstract
Using a large number of numerical simulations we examine the steady state of rotating turbulent flows in triple periodic domains, varying the Rossby number 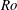 $Ro$ (that measures the inverse rotation rate) and the Reynolds number
$Ro$ (that measures the inverse rotation rate) and the Reynolds number 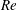 $Re$ (that measures the strength of turbulence). The examined flows are sustained by either a helical or a non-helical Roberts force, that is invariant along the axis of rotation. The forcing acts at a wavenumber
$Re$ (that measures the strength of turbulence). The examined flows are sustained by either a helical or a non-helical Roberts force, that is invariant along the axis of rotation. The forcing acts at a wavenumber 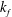 $k_{f}$ such that
$k_{f}$ such that 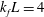 $k_{f}L=4$, where
$k_{f}L=4$, where  $2\unicode[STIX]{x03C0}L$ is the size of the domain. Different flow behaviours were obtained as the parameters are varied. Above a critical rotation rate the flow becomes quasi-two-dimensional and transfers energy to the largest scales of the system, forming large coherent structures known as condensates. We examine the behaviour of these condensates and their scaling properties close to and away from this critical rotation rate. Close to the critical rotation rate the system transitions supercritically to the condensate state, displaying a bimodal behaviour oscillating randomly between an incoherent-turbulent state and a condensate state. Away from the critical rotation rate, it is shown that two distinct mechanisms can saturate the growth of the large-scale energy. The first mechanism is due to viscous forces and is similar to the saturation mechanism observed for the inverse cascade in two-dimensional flows. The second mechanism is independent of viscosity and relies on the breaking of the two-dimensionalization condition of the rotating flow. The two mechanisms predict different scaling with respect to the control parameters of the system (Rossby and Reynolds), which are tested with the present results of the numerical simulations. A phase space diagram in the
$2\unicode[STIX]{x03C0}L$ is the size of the domain. Different flow behaviours were obtained as the parameters are varied. Above a critical rotation rate the flow becomes quasi-two-dimensional and transfers energy to the largest scales of the system, forming large coherent structures known as condensates. We examine the behaviour of these condensates and their scaling properties close to and away from this critical rotation rate. Close to the critical rotation rate the system transitions supercritically to the condensate state, displaying a bimodal behaviour oscillating randomly between an incoherent-turbulent state and a condensate state. Away from the critical rotation rate, it is shown that two distinct mechanisms can saturate the growth of the large-scale energy. The first mechanism is due to viscous forces and is similar to the saturation mechanism observed for the inverse cascade in two-dimensional flows. The second mechanism is independent of viscosity and relies on the breaking of the two-dimensionalization condition of the rotating flow. The two mechanisms predict different scaling with respect to the control parameters of the system (Rossby and Reynolds), which are tested with the present results of the numerical simulations. A phase space diagram in the 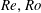 $Re,Ro$ parameter plane is sketched.
$Re,Ro$ parameter plane is sketched.
- Type
- JFM Papers
- Information
- Copyright
- © 2018 Cambridge University Press
References
- 49
- Cited by



