Article contents
Compressibility effects on the structural evolution of transitional high-speed planar wakes
Published online by Cambridge University Press: 28 April 2016
Abstract
The compressibility effects on the structural evolution of the transitional high-speed planar wake are studied. The relative Mach number (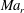 $Ma_{r}$) of the laminar base flow modifies two fundamental features of planar wake transition: (i) the characteristic length scale defined by the most unstable linear mode; and (ii) the domain of influence of the structures within the staggered two-dimensional vortex array. Linear stability results reveal a reduced growth (approximately 30 % reduction up to
$Ma_{r}$) of the laminar base flow modifies two fundamental features of planar wake transition: (i) the characteristic length scale defined by the most unstable linear mode; and (ii) the domain of influence of the structures within the staggered two-dimensional vortex array. Linear stability results reveal a reduced growth (approximately 30 % reduction up to 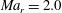 $Ma_{r}=2.0$) and a quasilinear increase of the wavelength of the most unstable, two-dimensional instability mode (approximately 20 % longer over the same
$Ma_{r}=2.0$) and a quasilinear increase of the wavelength of the most unstable, two-dimensional instability mode (approximately 20 % longer over the same 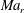 $Ma_{r}$ range) with increasing
$Ma_{r}$ range) with increasing 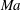 $Ma$. The primary wavelength defines the length scale imposed on the emerging transitional structures; naturally, a longer wavelength results in rollers with a greater streamwise separation and hence also larger circulation. A reduction of the growth rate and an increase of the principal wavelength results in a greater ellipticity of the emerging rollers. Compressibility effects also modify the domain of influence of the transitional structures through an increased cross-wake and inhibited streamwise communication as characteristic paths between rollers are deflected due to local
$Ma$. The primary wavelength defines the length scale imposed on the emerging transitional structures; naturally, a longer wavelength results in rollers with a greater streamwise separation and hence also larger circulation. A reduction of the growth rate and an increase of the principal wavelength results in a greater ellipticity of the emerging rollers. Compressibility effects also modify the domain of influence of the transitional structures through an increased cross-wake and inhibited streamwise communication as characteristic paths between rollers are deflected due to local 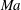 $Ma$ gradients. The reduced streamwise domain of influence impedes roller pairing and, for a sufficiently large relative
$Ma$ gradients. The reduced streamwise domain of influence impedes roller pairing and, for a sufficiently large relative 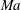 $Ma$, pairing is completely suppressed. Thus, we observe an increased two-dimensionality with increasing Mach number: directly contrasting the increasing three-dimensional effects in high-speed mixing layers. Temporally evolving direct numerical simulations conducted at
$Ma$, pairing is completely suppressed. Thus, we observe an increased two-dimensionality with increasing Mach number: directly contrasting the increasing three-dimensional effects in high-speed mixing layers. Temporally evolving direct numerical simulations conducted at 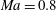 $Ma=0.8$ and 2.0, for Reynolds numbers up to 3000, support the physical insight gained from linear stability and vortex dynamics studies.
$Ma=0.8$ and 2.0, for Reynolds numbers up to 3000, support the physical insight gained from linear stability and vortex dynamics studies.
- Type
- Papers
- Information
- Copyright
- © 2016 Cambridge University Press
References
- 12
- Cited by



