Article contents
Compressibility effects on energy exchange mechanisms in a spatially developing plane free shear layer
Published online by Cambridge University Press: 12 January 2021
Abstract
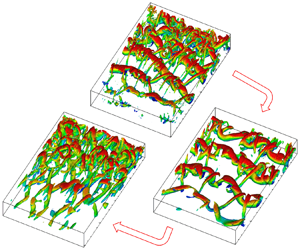
The compressibility effects on energy exchange mechanisms in a three-dimensional, spatially developing plane free shear layer are investigated via data produced by direct numerical simulation. The compressible shear layer is simulated using a high-order discontinuous spectral element method for convective Mach numbers  $M_c = 0.3$, 0.5 and 0.7. The energy exchange mechanisms in the flow are examined by analysing the budget terms of mean kinetic, internal and turbulent kinetic energy transport equations, in both transition and turbulent regions. The results show that turbulent production, turbulent viscous dissipation, mean viscous dissipation, pressure dilatation and enthalpic production are the main mechanisms responsible for energy exchange among different forms of energy. The effects of compressibility on energy transfer mechanisms are studied based on the analyses of those five budget terms. The primary budget terms evolve differently in the transition and turbulent regions and change significantly for varying compressibility. In the transition region, a double-peak variation becomes a single peak in the streamwise profile of the turbulent production as
$M_c = 0.3$, 0.5 and 0.7. The energy exchange mechanisms in the flow are examined by analysing the budget terms of mean kinetic, internal and turbulent kinetic energy transport equations, in both transition and turbulent regions. The results show that turbulent production, turbulent viscous dissipation, mean viscous dissipation, pressure dilatation and enthalpic production are the main mechanisms responsible for energy exchange among different forms of energy. The effects of compressibility on energy transfer mechanisms are studied based on the analyses of those five budget terms. The primary budget terms evolve differently in the transition and turbulent regions and change significantly for varying compressibility. In the transition region, a double-peak variation becomes a single peak in the streamwise profile of the turbulent production as  $M_c$ increases from 0.3 to 0.7, due to significant changes in the vortex pairing structures. The shear layer centre slightly shifts to the high-speed side due to the appearance of the velocity deficit. The velocity deficit presence distance (VDPD) becomes longer as compressibility increases. However, in the turbulent region, the cross-stream profiles of the main budget terms significantly shift to the low-speed side because of the asymmetric mass entrainment and shift even further as
$M_c$ increases from 0.3 to 0.7, due to significant changes in the vortex pairing structures. The shear layer centre slightly shifts to the high-speed side due to the appearance of the velocity deficit. The velocity deficit presence distance (VDPD) becomes longer as compressibility increases. However, in the turbulent region, the cross-stream profiles of the main budget terms significantly shift to the low-speed side because of the asymmetric mass entrainment and shift even further as  $M_c$ increases.
$M_c$ increases.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 12
- Cited by



