Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-01T02:55:00.500Z Has data issue: false hasContentIssue false
  • English
  • Français

Comparison between two- and three-dimensional Rayleigh–Bénard convection

Published online by Cambridge University Press:  04 November 2013

Erwin P. van der Poel ,
Richard J. A. M. Stevens  and
Detlef Lohse
Erwin P. van der Poel*
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O Box 217, 7500 AE Enschede, The Netherlands
Richard J. A. M. Stevens
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O Box 217, 7500 AE Enschede, The Netherlands Department of Mechanical Engineering, Johns Hopkins University, Baltimore, Maryland 21218, USA
Detlef Lohse
Affiliation:
Department of Science and Technology and J.M. Burgers Center for Fluid Dynamics, University of Twente, P.O Box 217, 7500 AE Enschede, The Netherlands
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

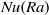Two-dimensional and three-dimensional Rayleigh–Bénard convection is compared using results from direct numerical simulations and previous experiments. The phase diagrams for both cases are reviewed. The differences and similarities between two- and three-dimensional convection are studied using $Nu(Ra)$ for 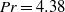$\mathit{Pr}= 4. 38$ and 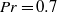$\mathit{Pr}= 0. 7$ and 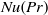$Nu(Pr)$ for 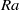$Ra$ up to 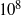$1{0}^{8} $. In the 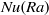$Nu(Ra)$ scaling at higher 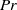$Pr$, two- and three-dimensional convection is very similar, differing only by a constant factor up to 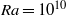$\mathit{Ra}= 1{0}^{10} $. In contrast, the difference is large at lower 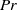$Pr$, due to the strong roll state dependence of 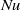$Nu$ in two dimensions. The behaviour of 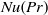$Nu(Pr)$ is similar in two and three dimensions at large 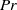$Pr$. However, it differs significantly around 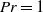$\mathit{Pr}= 1$. The Reynolds number values are consistently higher in two dimensions and additionally converge at large 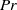$Pr$. Finally, the thermal boundary layer profiles are compared in two and three dimensions.

JFM classification

Turbulent Flows: Turbulent Flows Turbulent Flows: Turbulent convection
Type
Papers
Information
Journal of Fluid Mechanics , Volume 736 , 10 December 2013 , pp. 177 - 194
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ahlers, G., Bodenschatz, E., Funfschilling, D. & Hogg, J. 2009a Turbulent Rayleigh–Bénard convection for a Prandtl number of 0.67. J. Fluid. Mech. 641, 157–167.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009b Heat transfer and large-scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503.Google Scholar
Ahlers, G., He, X., Funfschilling, D. & Bodenschatz, E. 2012 Heat transport by turbulent Rayleigh–Bénard convection for $Pr= 0. 8$ and $3\times 1{0}^{12} \lesssim Ra\lesssim 1{0}^{15} $ : aspect ratio $\Gamma = 0. 50$ . New J. Phys. 14, 103012.Google Scholar
Bailon-Cuba, J., Emran, M. S. & Schumacher, J. 2010 Aspect ratio dependence of heat transfer and large-scale flow in turbulent convection. J. Fluid Mech. 655, 152–173.Google Scholar
Brown, E., Funfschilling, D., Nikolaenko, A. & Ahlers, G. 2005 Heat transport in turbulent Rayleigh–Bénard convection: effect of finite top- and bottom-plate conductivities. Phys. Fluids 17, 075108.Google Scholar
Burr, U., Kinzelbach, W. & Tsinober, A. 2003 Is the turbulent wind in convective flows driven by fluctuations? Phys. Fluids 15, 2313–2320.Google Scholar
Busse, F. H. 1978 Non-linear properties of thermal convection. Rep. Prog. Phys. 41, 1929–1967.CrossRefGoogle Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X. Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chandra, M. & Verma, M. K. 2011 Dynamics and symmetries of flow reversals in turbulent convection. Phys. Rev. E 83, 067303.CrossRefGoogle ScholarPubMed
Chaumat, S., Castaing, B. & Chilla, F. 2002 Rayleigh–Bénard cells: influence of plate properties. In Advances in Turbulence IX (ed. Castro, I. P., Hancock, P. E. & Thomas, T. G.), International Center for Numerical Methods in Engineering, CIMNE.Google Scholar
Chavanne, X., Chilla, F., Chabaud, B., Castaing, B. & Hebral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.CrossRefGoogle Scholar
DeLuca, E. E., Werne, J., Rosner, R. & Cattaneo, F. 1990 Numerical simulations of soft and hard turbulence: preliminary results for two-dimensional convection. Phys. Rev. Lett. 64, 2370–2373.CrossRefGoogle ScholarPubMed
Fleischer, A. S. & Goldstein, R. J. 2002 High-Rayleigh-number convection of pressurized gases in a horizontal enclosure. J. Fluid Mech. 469, 1–12.CrossRefGoogle Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92, 194502.Google Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical cells with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying view. J. Fluid. Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl number. Phys. Rev. Lett. 86, 3316–3319.Google Scholar
Grossmann, S. & Lohse, D. 2002 Prandtl and Rayleigh number dependence of the Reynolds number in turbulent thermal convection. Phys. Rev. E 66, 016305.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.CrossRefGoogle Scholar
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett 108, 024502.Google Scholar
Johnston, H. & Doering, C. R. 2009 Comparison of turbulent thermal convection between conditions of constant temperature and constant flux. Phys. Rev. Lett. 102, 064501.CrossRefGoogle ScholarPubMed
Kraichnan, R. 1967 Inertial ranges in two-dimensional turbulence. Phys. Fluids 10, 1417.Google Scholar
Lakkaraju, R., Stevens, R. J. A. M., Verzicco, R., Grossmann, S., Prosperetti, A., Sun, C. & Lohse, D. 2012 Spatial distribution of heat flux and fluctuations in turbulent Rayleigh–Bénard convection. Phys. Rev. E 86, 056315.CrossRefGoogle ScholarPubMed
Niemela, J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.Google Scholar
van der Poel, E. P., Stevens, R. J. A. M. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. E 84, 045303(R).Google Scholar
van der Poel, E. P., Stevens, R. J. A. M., Sugiyama, K. & Lohse, D. 2012 Flow states in two-dimensional Rayleigh–Bénard convection as a function of aspect-ratio and Rayleigh number. Phys. Fluids 24, 085104.Google Scholar
Pohlhausen, K. 1921 Zur nährungsweisen Integration der Differentialgleichung der laminaren Grenzschicht. Z. Angew. Math. Mech. 1, 252–268.CrossRefGoogle Scholar
Roberts, G. O. 1979 Fast viscous Bénard convection. Geophys. Astrophys. Fluid Dyn. 12, 235–272.Google Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.Google Scholar
Scheel, J., Kim, E. & White, K. 2012 Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid. Mech. 711, 281–305.Google Scholar
Schmalzl, J., Breuer, M., Wessling, S. & Hansen, U. 2004 On the validity of two-dimensional numerical approaches to time-dependent thermal convection. Europhys. Lett. 67, 390–396.CrossRefGoogle Scholar
Shi, N., Emran, M. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid. Mech. 706, 5–33.Google Scholar
Shishkina, O., Stevens, R. J. A. M., Grossmann, S. & Lohse, D. 2010 Boundary layer structure in turbulent thermal convection and its consequences for the required numerical resolution. New J. Phys. 12, 075022.CrossRefGoogle Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.Google Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh number convection. Phys. Rev. A 42, 3650–3653.Google Scholar
Stevens, R. J. A. M., van der Poel, E. P., Grossmann, S. & Lohse, D. 2013 The unifying theory of scaling in thermal convection: the updated prefactors. J. Fluid. Mech. 730, 295–308.Google Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.CrossRefGoogle Scholar
Stevens, R. J. A. M., Clercx, H. J. H. & Lohse, D. 2010a Optimal Prandtl number for heat transfer in rotating Rayleigh–Bénard convection. New J. Phys. 12, 075005.Google Scholar
Stevens, R. J. A. M., Lohse, D. & Verzicco, R. 2011a Prandtl number dependence of heat transport in high Rayleigh number thermal convection. J. Fluid. Mech. 688, 31–43.CrossRefGoogle Scholar
Stevens, R. J. A. M., Overkamp, J., Lohse, D. & Clercx, H. J. H. 2011b Effect of aspect-ratio on vortex distribution and heat transfer in rotating Rayleigh–Bénard. Phys. Rev. E 84, 056313.Google Scholar
Stevens, R. J. A. M., Verzicco, R. & Lohse, D. 2010b Radial boundary layer structure and Nusselt number in Rayleigh–Bénard convection. J. Fluid. Mech. 643, 495–507.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2007 Non-Oberbeck–Boussinesq effects in Rayleigh–Bénard convection: beyond boundary-layer theory. Europhys. Lett. 80, 34002.Google Scholar
Sugiyama, K., Calzavarini, E., Grossmann, S. & Lohse, D. 2009 Flow organization in two-dimensional non-Oberbeck–Boussinesq Rayleigh–Bénard convection in water. J. Fluid Mech. 637, 105–135.Google Scholar
Sugiyama, K., Ni, R., Stevens, R. J. A. M., Chan, T. S., Zhou, S.-Q., Xi, H.-D., Sun, C., Grossmann, S., Xia, K.-Q. & Lohse, D. 2010 Flow reversals in thermally driven turbulence. Phys. Rev. Lett. 105, 034503.CrossRefGoogle ScholarPubMed
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google Scholar
Urban, P., Hanzelka, P., Kralik, T., Musilova, V., Srnka, A. & Skrbek, L. 2012 Effect of boundary layers asymmetry on heat transfer efficiency in turbulent Rayleigh–Bénard convection at very high Rayleigh numbers. Phys. Rev. Lett. 109, 154301.Google Scholar
Urban, P., Musilová, V. & Skrbek, L. 2011 Efficiency of heat transfer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 107, 014302.CrossRefGoogle ScholarPubMed
Verzicco, R. & Camussi, R. 1999 Prandtl number effects in convective turbulence. J. Fluid Mech. 383, 55–73.CrossRefGoogle Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
Verzicco, R. & Orlandi, P. 1996 A finite-difference scheme for three-dimensional incompressible flow in cylindrical coordinates. J. Comput. Phys. 123, 402–413.Google Scholar
Vincent, A. P. & Yuen, D. A. 2000 Transition to turbulent thermal convection beyond $Ra= 1{0}^{10} $ detected in numerical simulations. Phys. Rev. E 61, 5241.CrossRefGoogle Scholar
Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid. Mech. 697, 336–366.CrossRefGoogle Scholar
Weiss, S., Stevens, R. J. A. M., Zhong, J.-Q., Clercx, H. J. H., Lohse, D. & Ahlers, G. 2010 Finite-size effects lead to supercritical bifurcations in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 105, 224501.Google Scholar
Werne, J. 1993 Structure of hard-turbulent convection in two-dimensions: numerical evidence. Phys. Rev. E 48, 1020–1035.Google Scholar
Werne, J., DeLuca, E. E., Rosner, R. & Cattaneo, F. 1991 Development of hard-turbulence convection in two dimensions: numerical evidence. Phys. Rev. Lett. 67, 3519.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Zhong, J.-Q., Stevens, R. J. A. M., Clercx, H. J. H., Verzicco, R., Lohse, D. & Ahlers, G. 2009 Prandtl-, Rayleigh-, and Rossby-number dependence of heat transport in turbulent rotating Rayleigh–Bénard convection. Phys. Rev. Lett. 102, 044502.Google Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid. Mech. 664, 297–312.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.Google Scholar