Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-07T22:55:09.827Z Has data issue: false hasContentIssue false
  • English
  • Français

Coherent structure identification in turbulent channel flow using latent Dirichlet allocation

Published online by Cambridge University Press:  11 June 2021

Mohamed Frihat ,
Bérengère Podvin Open the ORCID record for Bérengère Podvin [Opens in a new window] ,
Lionel Mathelin ,
Yann Fraigneau  and
François Yvon
Mohamed Frihat
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400Orsay, France
Bérengère Podvin*
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400Orsay, France
Lionel Mathelin
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400Orsay, France
Yann Fraigneau
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400Orsay, France
François Yvon
Affiliation:
Université Paris-Saclay, CNRS, Laboratoire Interdisciplinaire des Sciences du Numérique, 91400Orsay, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

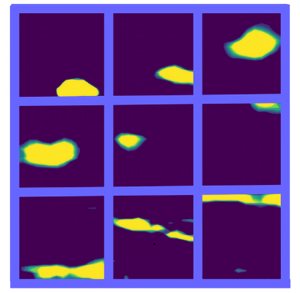
Identification of coherent structures is an essential step to describe and model turbulence generation mechanisms in wall-bounded flows. To this end, we present a clustering method based on latent Dirichlet allocation (LDA), a generative probabilistic model for collection of discrete data. The method is applied to a set of snapshots featuring the Reynolds stress ($Q_-$ events) for a turbulent channel flow at a moderate Reynolds number $R_{\tau }=590$. Both two- and three-dimensional analysis show that LDA provides a robust and compact flow description in terms of a combination of motifs, which are latent variables inferred from the set of snapshots. We find that the characteristics of the motifs scale with the wall distance, in agreement with the wall-attached eddy hypothesis of Townsend (Physics of Fluids, 1961, pp. 97–120). Latent Dirichlet allocation motifs can be used to reconstruct fields with an efficiency that can be compared with the proper orthogonal decomposition (POD). Moreover, the LDA model makes it possible to generate a collection of synthetic fields that captures the intermittent characteristics of the original dataset more clearly than its POD-generated counterpart. These findings highlight the potential of LDA for turbulent flow analysis, efficient reconstruction of actual fields and production of a new field with suitable statistics.

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 920 , 10 August 2021 , A27
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alamo, J.C.D., Jimenez, J., Zandonade, P. & Moser, R.D. 2006 Self-similar vortex clusters in the turbulent logarithmic region. J. Fluid Mech. 561, 329–358.CrossRefGoogle Scholar
Aubert, A.H., Tavenard, R., Emonet, R., de Lavenne, A., Malinowski, S., Guyet, T., Quiniou, R., Odobez, J.-M., Merot, P. & Gascuel-Odoux, C. 2013 Clustering flood events from water quality time series using latent Dirichlet allocation model. Water Resour. Res. 49 (12), 8187–8199.CrossRefGoogle Scholar
Baars, W.J., Hutchins, N. & Marusic, I. 2017 Self-similarity of wall-attached turbulence in boundary layers. J. Fluid Mech. 823, R2.CrossRefGoogle Scholar
Blei, D., Ng, A. & Jordan, M.I. 2003 Latent Dirichlet allocation. J. Machine Learning Res. 3, 993–1022.Google Scholar
Brunton, S.L., Noack, B.R. & Koumoutsakos, P. 2020 Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52 (1), 477–508.CrossRefGoogle Scholar
Cantwell, B.J. 1981 Organized motion in turbulent flow. Annu. Rev. Fluid Mech. 13, 457–515.CrossRefGoogle Scholar
Chandran, D., Monty, J.P. & Marusic, I. 2020 Spectral-scaling-based extension to the attached eddy model of wall turbulence. Phys. Rev. Fluids 5, 104606.CrossRefGoogle Scholar
Cheng, C., Li, W., Lozano-Durán, A. & Liu, H. 2020 Uncovering townsend's wall-attached eddies in low-Reynolds-number wall turbulence. J. Fluid Mech. 889, A29.CrossRefGoogle Scholar
Dempster, A.P., Laird, N.M. & Rubin, D.B. 1977 Maximum likelihood from incomplete data via the em algorithm. J. R. Stat. Soc. B 39 (1), 1–38.Google Scholar
Dennis, J.C.D. 2015 Coherent structures in wall-bounded turbulence. An. Acad. Bras. Cienc. 87 (2), 161–193.CrossRefGoogle ScholarPubMed
Ding, C., He, X. & Simon, H.D. 2005 On the equivalence of nonnegative matrix factorization and spectral clustering. In SIAM International Conference on Data Mining (ed. H. Kargupta , J. Srivastava , C. Kamath & A. Goodman). SIAM.CrossRefGoogle Scholar
Eckart, C. & Young, G. 1936 The approximation of one matrix by another of lower rank. Psychometrika 1 (3), 211–218.CrossRefGoogle Scholar
Faleiros, T. & Lopes, A. 2016 On the equivalence between algorithms for non-negative matrix factorization and latent dirichlet allocation. In ESANN European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning XXIV, Bruges. Louvain-la-Neuve Ciaco.Google Scholar
Flores, O. & Jimenez, J. 2010 Hierarchy of minimal flow units in the logarithmic layer. Phys. Fluids 22, 071704.CrossRefGoogle Scholar
Griffiths, T.L. & Steyvers, M. 2002 A probabilistic approach to semantic representation. In Proceedings of the 24th Annual Conference of the Cognitive Science Society (ed. W.D. Gray & C.D. Schunn). Routledge, Taylor & Francis.Google Scholar
Griffiths, T.L. & Steyvers, M. 2004 Finding scientific topics. Proc. Natl Acad. Sci. 101 (suppl 1), 5228–5235.CrossRefGoogle ScholarPubMed
Hellström, L.H.O., Marusic, I. & Smits, A.J. 2016 Self-similarity of the large-scale motions in turbulent pipe flow. J. Fluid Mech. 792, R1.CrossRefGoogle Scholar
Hofmann, M.D., Blei, D.M., Wang, C. & Paisley, J. 2013 Stochastic variational inference. J. Machine Learning Res. 14, 1303–1347.Google Scholar
Hofmann, T. 1999 Probabilistic latent semantic analysis. In Proceedings of Uncertainty in Artificial Intelligence (ed. K.B. Laskey & H. Prade). UAI99. Morgan Kaufmann.Google Scholar
Holmes, P., Lumley, J.L. & Berkooz, G. 1996 Turbulence, Coherent Structures, Dynamical Systems and Symmetry. Cambridge University Press.CrossRefGoogle Scholar
Hu, R., Yang, X.I.A. & Zheng, X. 2020 Wall-attached and wall-detached eddies in wall-bounded turbulent flows. J. Fluid Mech. 885, A30.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2018 Wall-attached structures of velocity fluctuations in a turbulent boundary layer. J. Fluid Mech. 856, 958–983.CrossRefGoogle Scholar
Hwang, J. & Sung, H.J. 2019 Wall-attached clusters for the logarithmic velocity law in turbulent pipe flow. Phys. Fluids 31 (5), 055109.Google Scholar
Jimenez, J. 2013 Near-wall turbulence. Phys. Fluids 25 (1), 101302.CrossRefGoogle Scholar
Jimenez, J. 2018 Coherent structures in wall-bounded turbulence. J. Fluid Mech. 842, P1.CrossRefGoogle Scholar
Johnson, P.L. & Meneveau, C. 2017 Turbulence intermittency in a multiple-time-scale Navier–Stokes-based reduced model. Phys. Rev. Fluids 2, 072601.CrossRefGoogle Scholar
Kim, H.T., Kline, S.J. & Reynolds, W.C. 1971 The production of turbulence near a smooth wall in a turbulent boundary layer. J. Fluid Mech. 50 (1), 133–160.CrossRefGoogle Scholar
Kline, S.J., Reynolds, W.C., Schraub, F.A. & Runstadler, P.W. 1967 The structure of turbulent boundary layers. J. Fluid Mech. 30 (4), 741–773.CrossRefGoogle Scholar
Lloyd, S.P. 1982 Least squares quantization in PCM. IEEE Trans. Inf. Theory 28 (2), 129–137.CrossRefGoogle Scholar
Lozano-Duran, A., Flores, O. & Jimenez, J. 2012 The three-dimensional structure of momentum transfer in turbulent channels. J. Fluid Mech. 524, 1–31.Google Scholar
Lumley, J.L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. A.M. Iaglom & V.I. Tatarski), pp. 221–227. Nauka.Google Scholar
MacQueen, J. 1967 Some methods for classification and analysis of multivariate observations. In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, Volume 1: Statistics (ed. L.M. Le Cam & J. Neyman), pp. 281–297. University of California Press.Google Scholar
Marusic, I. & Monty, J.P. 2019 Attached eddy model of wall turbulence. Annu. Rev. Fluid Mech. 51 (1), 49–74.CrossRefGoogle Scholar
Moser, R., Kim, J. & Mansour, N.N. 1999 Direct numerical simulation of turbulent channel flow up to $Re_{\tau }=590$. Phys. Fluids 11 (4), 943.CrossRefGoogle Scholar
Muralidhar, S., Podvin, B., Mathelin, L. & Fraigneau, Y. 2019 Spatio-temporal proper orthogonal decomposition of turbulent channel flow. J. Fluid Mech. 864, 614–639.CrossRefGoogle Scholar
Pedregosa, F., et al. 2011 Scikit-learn: machine learning in Python. J. Machine Learning Res. 12, 2825–2830.Google Scholar
Perry, A.E. & Chong, M.S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.CrossRefGoogle Scholar
Perry, A.E. & Marusic, I. 1995 A wall-wake model for the turbulent structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Philip, J., Meneveau, C., de Silva, C.M. & Marusic, I. 2014 Multiscale analysis of fluxes at the turbulent/non-turbulent interface in high Reynolds number boundary layers. Phys. Fluids 26 (1), 015105.CrossRefGoogle Scholar
Podvin, B. & Fraigneau, Y. 2017 A few thoughts on proper orthogonal decomposition in turbulence. Phys. Fluids 29, 531.CrossRefGoogle Scholar
Podvin, B., Fraigneau, Y., Jouanguy, J. & Laval, J.P. 2010 On self-similarity in the inner wall layer of a turbulent channel flow. Trans. ASME J. Fluids Engng 132 (4), 41202.CrossRefGoogle Scholar
Robinson, S.K. 1991 Coherent motions in the turbulent boundary layer. Annu. Rev. Fluid Mech. 23, 601–639.CrossRefGoogle Scholar
Sharma, A.S. & McKeon, B.J. 2013 On coherent structure in wall turbulence. J. Fluid Mech. 728, 196–238.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures part i: coherent structures. Q. Appl. Maths 45 (3), 561–571.CrossRefGoogle Scholar
Stanislas, M., Perret, L. & Foucaut, J.M. 2008 Vortical structures in the turbulent boundary layer: a possible route to a universal representation. J. Fluid Mech. 602, 327–382.CrossRefGoogle Scholar
Tipping, M.E. & Bishop, C.M. 1999 Probabilistic principal component analysis. J. R. Stat. Soc. B 61 (3), 611–622.CrossRefGoogle Scholar
Townsend, A.A. 1947 Measurements in the turbulent wake of a cylinder. Proc. R. Soc. Lond. A 190, 551–561.Google Scholar
Townsend, A.A. 1961 Equilibrium layers and wall turbulence. J. Fluid Mech. 11 (1), 97–120.CrossRefGoogle Scholar
Wallace, J.M., Eckelmann, H. & Brodkey, R.S. 1972 The wall region in turbulent shear flow. J. Fluid Mech. 54 (1), 39–48.CrossRefGoogle Scholar
Willmarth, W.W. & Lu, S.S. 1972 Structure of the Reynolds stress near the wall. J. Fluid Mech. 55 (1), 65–92.CrossRefGoogle Scholar
Woodcock, J.D. & Marusic, I. 2015 The statistical behavior of attached eddies. Phys. Fluids 27, 015104.CrossRefGoogle Scholar
Zhou, J., Adrian, R.J., Balachandar, S. & Kendall, T.M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 173–217.CrossRefGoogle Scholar