Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T12:04:49.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Coalescence of drops with mobile interfaces in a quiescent fluid

Published online by Cambridge University Press:  11 July 2013

M. B. Nemer ,
P. Santoro ,
X. Chen ,
J. Bławzdziewicz  and
M. Loewenberg
M. B. Nemer*
Affiliation:
Thermal & Fluid Experimental Science, Sandia National Laboratories, Albuquerque, NM 87185, USA
P. Santoro
Affiliation:
Jefferies International Limited, 68 Upper Thames Street, London EC4V 3BJ, UK
X. Chen
Affiliation:
Exotic Credit Derivative Trading, Citigroup, New York City, NY 10013, USA
J. Bławzdziewicz
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409-1021, USA
M. Loewenberg
Affiliation:
Department of Chemical and Environmental Engineering, Yale University, New Haven, CT 06520-8286, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A study on the axisymmetric near-contact motion of drops with tangentially mobile interfaces under the action of a body force in a quiescent fluid is described. A long-time asymptotic analysis is presented for small-deformation conditions. Under these conditions the drops are nearly spherical, except in the near-contact region, where a flattened thin film forms. According to our analysis, a hydrostatic dome does not form in the near-contact region at long times, in contrast to the assumption underlying all previous analyses of this problem. Instead, the shape of the film in the near-contact region results from the absence of tangential stresses acting on it. As a result, the long-time behaviour of the system is qualitatively different than previously predicted. According to the theory presented herein, the minimum film thickness (rim region) decays with time as 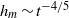${h}_{m} \sim {t}^{- 4/ 5} $, and the thickness at the centre of the film decays as 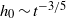${h}_{0} \sim {t}^{- 3/ 5} $, which is a faster decay than predicted by prior analyses based on a hydrostatic dome. Numerical thin-film simulations quantitatively confirm the predictions of our small-deformation theory. Boundary-integral simulations of the full two-drop problem suggest that the theory also describes qualitatively the long-time evolution under finite-deformation conditions.

JFM classification

Drops and Bubbles: Breakup/coalescence Drops and Bubbles: Drops Complex Fluids: Emulsions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 728 , 10 August 2013 , pp. 471 - 500
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aarts, D. G. A. L., Lekkerkerker, H. N. W., Guo, H., Wegdam, G. H. & Bonn, D. 2005 Hydrodynamics of droplet coalescence. Phys. Rev. Lett. 95, 164503.Google Scholar
Ascoli, E. P., Dandy, D. S. & Leal, L. G. 1990 Buoyancy-driven motion of a deformable drop toward a planar wall at low Reynolds number. J. Fluid Mech. 213, 287–311.Google Scholar
Brandenberger, H., Nussli, D., Piech, V. & Widmer, F. 1999 Monodisperse particle production: a method to prevent drop coalescence using electrostatic forces. J. Electrost. 45, 227–238.Google Scholar
Brown, A. H. & Hanson, C. 1967 Drop coalescence in liquid–liquid systems. Nature 214, 76–77.CrossRefGoogle Scholar
Chan, D., Klaseboer, E. & Manica, R. 2011 Film drainage and coalescence between deformable drops and bubbles. Soft Matt. 7, 2235–2264.Google Scholar
Chesters, A. K. 1991 The modelling of coalescence processes in fluid–liquid dispersions: a review of current understanding. Chem. Engng Res. Des. 69, 259–270.Google Scholar
Conner, J. N. & Horn, R. G. 2003 The influence of surface forces on thin film drainage between a fluid drop and a flat solid. Faraday Disc. 123, 193–206.Google Scholar
Cristini, V. & Tan, Y. C. 2004 Theory and numerical simulation of droplet dynamics in complex flows: a review. Lab on a Chip 4, 257–264.CrossRefGoogle ScholarPubMed
Davis, R. H., Schonberg, J. A. & Rallison, J. M. 1989 The lubrication force between two viscous drops. Phys. Fluids A 1, 77–81.CrossRefGoogle Scholar
Derjaguin, B. & Kussakov, M. 1939 Anomalous properties of thin poly-molecular films. Acta. Physicochim. USSR 10, 25–30.Google Scholar
Edwards, S. A., Carnie, S. L., Manor, O. & Chan, D. Y. C. 2009 Effects of internal flow and viscosity ratio on measurements of dynamic forces between deformable drops. Langmuir 25, 3352–3355.CrossRefGoogle ScholarPubMed
Eggers, J., Lister, J. R. & Stone, H. A. 1999 Coalescence of liquid drops. J. Fluid Mech. 401, 293–310.CrossRefGoogle Scholar
Eow, J. S., Ghadiri, M., Sharif, A. O. & Williams, T. J. 2001 Electrostatic enhancement of coalescence of water droplets in oil: a review of the current understanding. Chem. Engng J. 84, 173–192.CrossRefGoogle Scholar
Fortelny, I. & Zivny, A. 1998 Film drainage between droplets during their coalescence in quiescent polymer blends. Polymer 39, 2669–2675.Google Scholar
Frankel, S. P. & Mysels, K. J. 1962 On the dimpling during the approach of two interfaces. J. Phys. Chem. 66, 190–191.CrossRefGoogle Scholar
Gopinath, A. & Koch, D. 2002 Collision and rebound of small droplets in an incompressible continuum gas. J. Fluid Mech. 454, 145–201.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 1994 Table of Integrals, Series, and Products, chap. 8. Academic.Google Scholar
Hamaker, H. 1937 The London–Van der Waals attraction between spherical particles. Physica 4, 1058–1072.Google Scholar
Hartland, S. 1967 The approach of a liquid drop to a flat plate. Chem. Engng Sci. 22, 1675–1687.Google Scholar
Jansons, K. M. & Lister, J. R. 1988 The general solution of Stokes flow in a half-space as an integral of the velocity on the boundary. Phys. Fluids 31, 1321–1323.Google Scholar
Janssen, P. J. A., Anderson, P. D., Peters, G. W. M. & Meijer, H. E. H. 2006 Axisymmetric boundary integral simulations of film drainage between two viscous drops. J. Fluid Mech. 567, 65–90.Google Scholar
Jones, A. F. & Wilson, S. D. R. 1978 The film drainage problem in droplet coalescence. J. Fluid Mech. 87, 263–288.Google Scholar
Lai, A., Bremond, N. & Stone, H. A. 2009 Separation-driven coalescence of drops: an analytical criterion for the approach to contact. J. Fluid Mech. 632, 97–107.Google Scholar
Lekkerkerker, H. N. W., de Villeneuve, V. W. A., de Folter, J. W. J., Schmidt, M., Hennequin, Y., Bonn, D., Indekeu, J. O. & Aarts, D. G. A. L. 2008 Life at ultralow interfacial tension: wetting, waves and droplets in demixed colloid-polymer mixtures. Euro. Phys. J. B 64, 341–347.Google Scholar
Li, D. & Liu, S. 1996 Coalescence between small bubbles or drops in pure liquids. Langmuir 12, 5216–5220.Google Scholar
Lyu, S., Bates, F. & Macosko, C. 2002 Modelling of coalescence in polymer blends. AIChE J. 48, 7–14.CrossRefGoogle Scholar
Manga, M. & Stone, H. A. 1993 Buoyancy-driven interactions between two deformable viscous drops. J. Fluid Mech. 256, 647–683.Google Scholar
Manoharan, V. N., Imhof, A., Thorne, J. D. & Pine, D. J. 2001 Photonic crystals from emulsion templates. Adv. Mater. 13, 447–450.3.0.CO;2-4>CrossRefGoogle Scholar
Mehdi-Nejad, V., Mostaghimi, J. & Chandra, S. 2003 Air bubble entrapment under an impacting droplet. Phys. Fluids 15, 173–183.Google Scholar
Nemer, M. B. 2003 Near-contact motion of liquid drops in emulsions and foams. PhD thesis, Yale University.Google Scholar
Nemer, M., Chen, X., Papadopoulos, D., Bławzdziewicz, J. & Loewenberg, M. 2004 Hindered and enhanced coalescence of drops in Stokes flow. Phys. Rev. Lett. 92, 114501.Google Scholar
Nemer, M., Chen, X., Papadopoulos, D., Bławzdziewicz, J. B. & Loewenberg, M. 2007 Comment on two touching spherical drops in uniaxial extensional flow: analytical solution of the creeping flow problem. J. Colloid Interface Sci. 308, 1–3.Google Scholar
Pozrikidis, C. 1990 The deformation of a liquid drop moving normal to a plane wall. J. Fluid Mech. 215, 331–363.CrossRefGoogle Scholar
Pozrikidis, C. 1992 Boundary Integral and Singularity Methods for Linearized Viscous Flow. Cambridge University Press.Google Scholar
Pozrikidis, C. 2002 Expansion of a two-dimensional foam. Engng Anal. Bound. Elem. 26, 495–504.Google Scholar
Ratke, L. & Diefenbach, S. 1995 Liquid immiscible alloys. Mat. Sci. Engng R 263–347.Google Scholar
Rother, M. A., Zinchenko, A. Z. & Davis, R. H. 1997 Buoyancy-driven coalescence of slightly deformable drops. J. Fluid Mech. 346, 117–148.Google Scholar
Saboni, A., Gourdon, C. & Chesters, A. K. 1995 Drainage and rupture of partially mobile films during coalescence in liquid–liquid systems under a constant interaction force. J. Colloid Interface Sci. 175, 27–35.CrossRefGoogle Scholar
Santoro, P. 2007 Coalescence of drops with tangentially mobile interfaces: hydrodynamic effects of surfactant and ambient flow. PhD thesis, Yale University.Google Scholar
Santoro, P. & Loewenberg, M. 2009 The influence of ambient flow on drop coalescence. Ann. N.Y. Acad. Sci. 1161, 277–291.Google Scholar
Senee, J., Robillard, B. & Vignes-Adler, M. 1999 Films and foams of champagne wines. Food Hydrocolloids 13, 15–26.Google Scholar
Sundararaj, U. & Macosko, C. 1995 Drop breakup and coalescence in polymer blends: the effects of concentration and compatibilization. Macromolecules 28, 2647–2657.Google Scholar
Vaessen, G., Visschers, M. & Stein, H. 1996 Predicting catastrophic phase inversion on the basis of droplet coalescence kinetics. Langmuir 12, 875–882.Google Scholar
Vaynblat, D., Lister, J. & Witelski, T. 2001 Rupture of thin viscous films by van der Waals forces: evolution and self-similarity. Phys. Fluids 13, 1130–1140.Google Scholar
Verdier, C. & Brizard, M. 2002 Understanding droplet coalescence and its use to estimate interfacial tension. Rheol. Acta 41, 514–523.Google Scholar
Witelski, T. & Bernoff, A. J. 1999 Stability of self-similar solutions for van der Waals driven thin film rupture. Phys. Fluids 11, 2443–2445.CrossRefGoogle Scholar
Yang, H., Park, C. C., Hu, Y. T. & Leal, L. G. 2001 The coalescence of two equal-sized drops in a two-dimensional linear flow. Phys. Fluids 13, 1087–1106.Google Scholar
Yiantsios, S. G. & Davis, R. H. 1990 On the buoyancy-driven motion of a drop towards a rigid surface or a deformable interface. J. Fluid Mech. 217, 547–573.Google Scholar
Yiantsios, S. G. & Davis, R. H. 1991 Close approach and deformation of two viscous drops due to gravity and van der Waals forces. J. Colloid Interface Sci. 144, 412–433.CrossRefGoogle Scholar
Yoon, Y., Baldessari, F., Ceniceros, H. D. & Leal, L. G. 2007 Coalescence of two equal-sized deformable drops in an axisymmetric flow. Phys. Fluids 19, 102102.Google Scholar
Zhang, W. W. & Lister, J. R. 1999 Similarity solutions for van der Waals rupture of a thin film on a solid substrate. Phys. Fluids 11, 2454–2462.CrossRefGoogle Scholar
Supplementary material: PDF

Nemer et al. supplementary material

Appendix

Download Nemer et al. supplementary material(PDF)
PDF 47.8 KB