Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-12-01T09:16:13.308Z Has data issue: false hasContentIssue false
  • English
  • Français

Closure model for homogeneous isotropic turbulence in the Lagrangian specification of the flow field

Published online by Cambridge University Press:  23 February 2018

Makoto Okamura Open the ORCID record for Makoto Okamura [Opens in a new window]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes a new two-point closure model that is compatible with the Kolmogorov 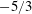$-5/3$ power law for homogeneous isotropic turbulence in an incompressible fluid using the Lagrangian specification of the flow field. A closed set of three equations was derived from the Navier–Stokes equation with no adjustable free parameters. The Kolmogorov constant and the skewness of the longitudinal velocity derivative were evaluated to be 1.779 and 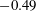$-0.49$, respectively, using the proposed model. The bottleneck effect was also reproduced in the near-dissipation range.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Isotropic turbulence Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 841 , 25 April 2018 , pp. 521 - 551
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

André, J. C. & Lesieur, M. 1977 Influence of helicity on evolution of isotropic turbulence at high Reynolds number. J. Fluid Mech. 81, 187–207.Google Scholar
Antonia, R. A., Tang, S. L., Djenidi, L. & Danaila, L. 2015 Boundedness of the velocity derivative skewness in various turbulent flows. J. Fluid Mech. 781, 727–744.CrossRefGoogle Scholar
Batchelor, G. K. 1949 Diffusion in a field of homogeneous turbulence I. Eulerian analysis. Austral. J. Sci. Res. A 2, 437–450.Google Scholar
Batchelor, G. K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Bos, W. J. T. & Bertoglio, J. P. 2006 A single-time two-point closure based on fluid particle displacements. Phys. Fluids 18, 031706.CrossRefGoogle Scholar
Bos, W. J. T., Chevillard, L., Scott, J. F. & Rubinstein, R. 2012 Reynolds number effect on the velocity increment skewness in isotropic turbulence. Phys. Fluids 24, 015108.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Donzis, D. A. & Sreenivasan, K. R. 2010 The bottleneck effect and the Kolmogorov constant in isotropic turbulence. J. Fluid Mech. 657, 171–188.Google Scholar
Durbin, P. A. & Pettersson Reif, B. A. 2011 Statistical Theory and Modeling for Turbulent Flows, 2nd edn. Wiley.Google Scholar
Edwards, S. F. & McComb, W. D. 1969 Statistical mechanics far from equilibrium. J. Phys. A 2, 157–171.Google Scholar
Falkovich, G. 1994 Bottleneck phenomenon in developed turbulence. Phys. Fluids 6, 1411–1414.CrossRefGoogle Scholar
Herring, J. R., Schertzer, D., Lesieur, M., Newman, G. R., Chollet, J. P. & Larcheveque, M. 1982 A comparative assessment of spectral closures as applied to passive scalar diffusion. J. Fluid Mech. 124, 411–437.Google Scholar
Kaneda, Y. 1981 Renormalized expansions in the theory of turbulence with the use of the Lagrangian position function. J. Fluid Mech. 107, 131–145.Google Scholar
Kaneda, Y. 1986 Inertial range structure of turbulent velocity and scalar fields in a Lagrangian renormalized approximation. Phys. Fluids 29, 701–708.Google Scholar
Kaneda, Y. 1993 Lagrangian and Eulerian time correlations in turbulence. Phys. Fluids A 5, 2835–2845.Google Scholar
Kaneda, Y., Ishihara, T. & Gotoh, K. 1999 Taylor expansions in powers of time of Lagrangian and Eulerian two-point two-time velocity correlations in turbulence. Phys. Fluids 11, 2154–2166.Google Scholar
Kida, S. & Goto, S. 1997 A Lagrangian direct-interaction approximation for homogeneous isotropic turbulence. J. Fluid Mech. 345, 307–345.Google Scholar
Kida, S. & Yanase, S. 1999 Turbulence Dynamics. Asakura Publishing (in Japanese).Google Scholar
Kraichnan, R. H. 1959 The structure of isotropic turbulence at very high Reynolds numbers. J. Fluid Mech. 5, 497–543.Google Scholar
Kraichnan, R. H. 1964 Kolmogorov’s hypotheses and Eulerian turbulence theory. Phys. Fluids 7, 1723–1734.Google Scholar
Kraichnan, R. H. 1965 Lagrangian-history closure approximation for turbulence. Phys. Fluids 8, 575–598.Google Scholar
Kraichnan, R. H. 1966 Isotropic turbulence and inertial-range structure. Phys. Fluids 9, 1728–1752.Google Scholar
Kraichnan, R. H. 1977 Eulerian and Lagrangian renormalization in turbulence theory. J. Fluid Mech. 83, 349–374.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer Academic Publishers.Google Scholar
Leslie, D. C. 1973 Developments in the Theory of Turbulence. Clarendon.Google Scholar
Lohse, D. & Müllergroeling, A. 1995 Bottleneck effects in turbulence: scaling phenomena in r versus p space. Phys. Rev. Lett. 74, 1747–1750.Google Scholar
McComb, W. D. 1978 A theory of time-dependent, isotropic turbulence. J. Phys. A 11, 613–632.Google Scholar
McComb, W. D. 1990 The Physics of Fluid Turbulence. Oxford University Press.CrossRefGoogle Scholar
McComb, W. D. & Shanmugasundaram, V. 1984 Numerical calculation of decaying isotropic turbulence using the LET theory. J. Fluid Mech. 143, 95–123.Google Scholar
McComb, W. D. & Yoffe, S. R. 2017 A formal derivation of the local energy transfer (LET) theory of homogeneous turbulence. J. Phys. A 50, 375501.Google Scholar
Millionshtchikov, M. D. 1941 On the theory of homogeneous isotropic turbulence. C. R. Dokl. Acad. Sci. URSS 32, 615–618.Google Scholar
Novikov, E. A. 1965 Functionals and random-force method in turbulence theory. Sov. Phys. JETP 20, 1290–1294.Google Scholar
Ogura, Y. 1963 A consequence of the zero-fourth-cumulant approximation in the decay of isotropic turbulence. J. Fluid Mech. 16, 33–40.Google Scholar
Orszag, S. A. 1977 Lectures on the statistical theory of turbulence. In Fluid Dynamics, pp. 235–374. Gordon and Breach.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Proudman, I. & Reid, W. H. 1954 On the decay of a normally distributed and homogeneous turbulent velocity field. Phil. Trans. R. Soc. Lond. A 247, 163–189.Google Scholar
Qian, J. 1983 Variational approach to the closure problem of turbulence theory. Phys. Fluids 26, 2098–2104.Google Scholar
Qian, J. 1984 Universal equilibrium range of turbulence. Phys. Fluids 27, 2229–2233.CrossRefGoogle Scholar
Qian, J. 1994 Skewness factor of turbulent velocity derivative. Acta Mechanica Sin. 10, 12–15.Google Scholar
Saddoughi, S. G. & Veeravalli, S. V. 1994 Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 268, 333–372.Google Scholar
Sreenivasan, K. R. 1995 On the universality of the Kolmogorov constant. Phys. Fluids 7, 2778–2784.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.CrossRefGoogle Scholar
Tatsumi, T. 1957 The theory of decay process of incompressible isotropic turbulence. Proc. R. Soc. Lond. A 239, 16–45.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Voth, G. A., Satyanarayan, K. & Bodenschatz, E. 1998 Lagrangian acceleration measurements at large Reynolds numbers. Phys. Fluids 10, 2268–2280.Google Scholar
Wyld, H. W. 1961 Formulation of the theory of turbulence in an incompressible fluid. Ann. Phys. 14, 143–165.Google Scholar
Yeung, P. K. 1994 Direct numerical simulation of two-particle relative diffusion in isotropic turbulence. Phys. Fluids 6, 3416–3428.Google Scholar
Yeung, P. K. 1997 One- and two-particle Lagrangian acceleration correlations in numerically simulated homogeneous turbulence. Phys. Fluids 9, 2981–2990.CrossRefGoogle Scholar
Yeung, P. K. & Pope, S. B. 1989 Lagrangian statistics from direct numerical simulations of isotropic turbulence. J. Fluid Mech. 207, 531–586.Google Scholar