Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Muschinski, Andreas
and
de Bruyn Kops, Stephen M.
2015.
Investigation of Hill’s optical turbulence model by means of direct numerical simulation.
Journal of the Optical Society of America A,
Vol. 32,
Issue. 12,
p.
2423.
Maffioli, A.
Brethouwer, G.
and
Lindborg, E.
2016.
Mixing efficiency in stratified turbulence.
Journal of Fluid Mechanics,
Vol. 794,
Issue. ,
Portwood, G. D.
de Bruyn Kops, S. M.
Taylor, J. R.
Salehipour, H.
and
Caulfield, C. P.
2016.
Robust identification of dynamically distinct regions in stratified turbulence.
Journal of Fluid Mechanics,
Vol. 807,
Issue. ,
Watanabe, Tomoaki
Riley, James J.
de Bruyn Kops, Stephen M.
Diamessis, Peter J.
and
Zhou, Qi
2016.
Turbulent/non-turbulent interfaces in wakes in stably stratified fluids.
Journal of Fluid Mechanics,
Vol. 797,
Issue. ,
Mortensen, Mikael
and
Langtangen, Hans Petter
2016.
High performance Python for direct numerical simulations of turbulent flows.
Computer Physics Communications,
Vol. 203,
Issue. ,
p.
53.
He, Ping
2016.
A high order finite difference solver for massively parallel simulations of stably stratified turbulent channel flows.
Computers & Fluids,
Vol. 127,
Issue. ,
p.
161.
Zhou, Qi
Taylor, John R.
and
Caulfield, C. P.
2017.
Self-similar mixing in stratified plane Couette flow for varying Prandtl number.
Journal of Fluid Mechanics,
Vol. 820,
Issue. ,
p.
86.
Pouquet, A.
Rosenberg, D.
Marino, R.
and
Herbert, C.
2018.
Scaling laws for mixing and dissipation in unforced rotating stratified turbulence.
Journal of Fluid Mechanics,
Vol. 844,
Issue. ,
p.
519.
Sujovolsky, N. E.
Mininni, P. D.
and
Pouquet, A.
2018.
Generation of turbulence through frontogenesis in sheared stratified flows.
Physics of Fluids,
Vol. 30,
Issue. 8,
Gregg, M.C.
D'Asaro, E.A.
Riley, J.J.
and
Kunze, E.
2018.
Mixing Efficiency in the Ocean.
Annual Review of Marine Science,
Vol. 10,
Issue. 1,
p.
443.
Basu, Abhik
and
Bhattacharjee, Jayanta K.
2019.
Kolmogorov or Bolgiano-Obukhov scaling: Universal energy spectra in stably stratified turbulent fluids.
Physical Review E,
Vol. 100,
Issue. 3,
Pouquet, Annick
2019.
Review of the monograph by Pierre Sagaut and Claude Cambon entitled Homogeneous Turbulence Dynamics.
Journal of Turbulence,
Vol. 20,
Issue. 3,
p.
240.
de Bruyn Kops, Stephen M.
and
Riley, James J.
2019.
The effects of stable stratification on the decay of initially isotropic homogeneous turbulence.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
787.
Okino, Shinya
and
Hanazaki, Hideshi
2019.
Decaying turbulence in a stratified fluid of high Prandtl number.
Journal of Fluid Mechanics,
Vol. 874,
Issue. ,
p.
821.
Bhattacharjee, Jayanta K
Kumar, Abhishek
and
Verma, Mahendra K
2019.
Turbulence in a stably stratified fluid: onset of global anisotropy as a function of the Richardson number.
Physica Scripta,
Vol. 94,
Issue. 12,
p.
125008.
Maffioli, Andrea
2019.
Asymmetry of vertical buoyancy gradient in stratified turbulence.
Journal of Fluid Mechanics,
Vol. 870,
Issue. ,
p.
266.
Lang, C. J.
and
Waite, Michael L.
2019.
Scale-dependent anisotropy in forced stratified turbulence.
Physical Review Fluids,
Vol. 4,
Issue. 4,
Portwood, G. D.
de Bruyn Kops, S. M.
and
Caulfield, C. P.
2019.
Asymptotic Dynamics of High Dynamic Range Stratified Turbulence.
Physical Review Letters,
Vol. 122,
Issue. 19,
Taylor, J. R.
de Bruyn Kops, S. M.
Caulfield, C. P.
and
Linden, P. F.
2019.
Testing the Assumptions Underlying Ocean Mixing Methodologies Using Direct Numerical Simulations.
Journal of Physical Oceanography,
Vol. 49,
Issue. 11,
p.
2761.
Pouquet, A.
Rosenberg, D.
Stawarz, J.E.
and
Marino, R.
2019.
Helicity Dynamics, Inverse, and Bidirectional Cascades in Fluid and Magnetohydrodynamic Turbulence: A Brief Review.
Earth and Space Science,
Vol. 6,
Issue. 3,
p.
351.
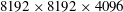 $8192\times 8192\times 4096$ grid points with buoyancy Reynolds numbers of
$8192\times 8192\times 4096$ grid points with buoyancy Reynolds numbers of 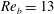 $\mathit{Re}_{b}=13$, 48 and 220. A simulation of isotropic homogeneous turbulence with a mean scalar gradient resolved on
$\mathit{Re}_{b}=13$, 48 and 220. A simulation of isotropic homogeneous turbulence with a mean scalar gradient resolved on 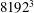 $8192^{3}$ grid points is used as a benchmark. The Prandtl number is unity. The stratified flows exhibit KOC scaling only for second-order statistics when
$8192^{3}$ grid points is used as a benchmark. The Prandtl number is unity. The stratified flows exhibit KOC scaling only for second-order statistics when 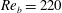 $\mathit{Re}_{b}=220$; the
$\mathit{Re}_{b}=220$; the 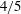 $4/5$ law is not observed. At lower
$4/5$ law is not observed. At lower  $\mathit{Re}_{b}$, the
$\mathit{Re}_{b}$, the 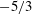 $-5/3$ slope in the spectra occurs at wavenumbers where the bottleneck effect occurs in unstratified cases, and KOC scaling is not observed in any of the structure functions. For the probability density functions (p.d.f.s) of the scalar and kinetic energy dissipation rates, the lognormal model works as well for the stratified cases with
$-5/3$ slope in the spectra occurs at wavenumbers where the bottleneck effect occurs in unstratified cases, and KOC scaling is not observed in any of the structure functions. For the probability density functions (p.d.f.s) of the scalar and kinetic energy dissipation rates, the lognormal model works as well for the stratified cases with 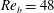 $\mathit{Re}_{b}=48$ and 220 as it does for the unstratified case. For lower
$\mathit{Re}_{b}=48$ and 220 as it does for the unstratified case. For lower 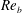 $\mathit{Re}_{b}$, the dominance of the vertical derivatives results in the p.d.f.s of the dissipation rates tending towards bimodal. The p.d.f.s of the dissipation rates locally averaged over spheres with radius in the inertial range tend towards bimodal regardless of
$\mathit{Re}_{b}$, the dominance of the vertical derivatives results in the p.d.f.s of the dissipation rates tending towards bimodal. The p.d.f.s of the dissipation rates locally averaged over spheres with radius in the inertial range tend towards bimodal regardless of 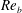 $\mathit{Re}_{b}$. There is no broad scaling range, but the intermittency exponents at length scales near the Taylor length are in the range of
$\mathit{Re}_{b}$. There is no broad scaling range, but the intermittency exponents at length scales near the Taylor length are in the range of 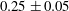 $0.25\pm 0.05$ and
$0.25\pm 0.05$ and 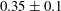 $0.35\pm 0.1$ for the velocity and scalar respectively.
$0.35\pm 0.1$ for the velocity and scalar respectively.


