Article contents
Characteristics of the pressure fluctuations generated in turbulent boundary layers over rough surfaces
Published online by Cambridge University Press: 20 November 2019
Abstract
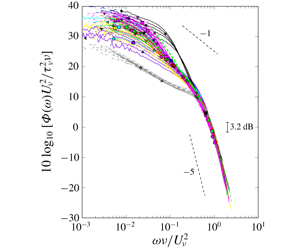
Experiments were carried out in high Reynolds number turbulent boundary layers over rough surfaces of diverse geometries. Roughness configurations varied in element height, distribution (random versus ordered), shape and spacing. Rough surfaces comprising of two superposed element geometries were also tested. All flows were free of transitional effects with  $Re_{\unicode[STIX]{x1D703}}$ upwards of 40 000 and
$Re_{\unicode[STIX]{x1D703}}$ upwards of 40 000 and  $\unicode[STIX]{x1D6FF}/k_{g}$ ratios above 73. The wall-pressure spectrum and turbulent velocity profiles revealed that the roughness element spacing has the greatest impact on the turbulent structures in the boundary layer. The high-frequency scaling on shear friction velocity,
$\unicode[STIX]{x1D6FF}/k_{g}$ ratios above 73. The wall-pressure spectrum and turbulent velocity profiles revealed that the roughness element spacing has the greatest impact on the turbulent structures in the boundary layer. The high-frequency scaling on shear friction velocity,  $U_{\unicode[STIX]{x1D708}}$, (Meyers et al.J. Fluid Mech., vol. 768, 2015, pp. 261–293) was validated and
$U_{\unicode[STIX]{x1D708}}$, (Meyers et al.J. Fluid Mech., vol. 768, 2015, pp. 261–293) was validated and  $U_{\unicode[STIX]{x1D708}}$ was shown to be the viscous contribution to the overall surface drag. An empirical formula for the pressure drag on roughness elements was developed to reflect the finding that the pressure drag is a function of only two variables: sparseness ratio
$U_{\unicode[STIX]{x1D708}}$ was shown to be the viscous contribution to the overall surface drag. An empirical formula for the pressure drag on roughness elements was developed to reflect the finding that the pressure drag is a function of only two variables: sparseness ratio  $(\unicode[STIX]{x1D706})$ and roughness Reynolds number
$(\unicode[STIX]{x1D706})$ and roughness Reynolds number  $(k_{g}^{+})$. Results also suggest that the viscous contribution to drag approaches a constant non-zero value at high Reynolds numbers, and ‘fully rough-wall flow’ may occur at higher
$(k_{g}^{+})$. Results also suggest that the viscous contribution to drag approaches a constant non-zero value at high Reynolds numbers, and ‘fully rough-wall flow’ may occur at higher  $k_{g}^{+}$ than previously thought.
$k_{g}^{+}$ than previously thought.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 11
- Cited by


