Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-28T17:06:23.390Z Has data issue: false hasContentIssue false
  • English
  • Français

The Burnett equations in cylindrical coordinates and their solution for flow in a microtube

Published online by Cambridge University Press:  16 June 2014

Narendra Singh  and
Amit Agrawal
Narendra Singh
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
Amit Agrawal*
Affiliation:
Department of Mechanical Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Burnett equations constitute a set of higher-order continuum equations. These equations are obtained from the Chapman–Enskog series solution of the Boltzmann equation while retaining second-order-accurate terms in the Knudsen number 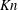$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Kn}$. The set of higher-order continuum models is expected to be applicable to flows in the slip and transition regimes where the Navier–Stokes equations perform poorly. However, obtaining analytical or numerical solutions of these equations has been noted to be particularly difficult. In the first part of this work, we present the full set of Burnett equations in cylindrical coordinates in three-dimensional form. The equations are reported in a generalized way for gas molecules that are assumed to be Maxwellian molecules or hard spheres. In the second part, a closed-form solution of these equations for isothermal Poiseuille flow in a microtube is derived. The solution of the equations is shown to satisfy the full Burnett equations up to 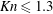$\mathit{Kn} \leq 1.3$ within an error norm of 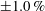${\pm }1.0\, \%$. The mass flow rate obtained analytically is shown to compare well with available experimental and numerical results. Comparison of the stress terms in the Burnett and Navier–Stokes equations is presented. The significance of the Burnett normal stress and its role in diffusion of momentum is brought out by the analysis. An order-of-magnitude analysis of various terms in the equations is presented, based on which a reduced model of the Burnett equations is provided for flow in a microtube. The Burnett equations in full three-dimensional form in cylindrical coordinates and their solution are not previously available.

JFM classification

Micro-/Nano-fluid dynamics: Micro-/Nano-fluid dynamics Micro-/Nano-fluid dynamics: Non-continuum effects Rarefied Gas Flow: Rarefied Gas Flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 751 , 25 July 2014 , pp. 121 - 141
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agrawal, A. & Dongari, N. 2012 Application of Navier–Stokes equations to high Knudsen number flow in a fine capillary. Intl J. Microscale Nanoscale Therm. Fluid Transp. Phenomena 3 (2), 125–130.Google Scholar
Agarwal, R. K., Yun, K. Y. & Balakrishnan, R. 2001 Beyond Navier–Stokes Burnett equations for flows in the continuum transition regime. Phys. Fluids 13, 3061–3085; (Erratum: 2002 Phys. Fluids 14, 1818).Google Scholar
Bao, F. & Lin, J. 2008 Burnett simulations of gas flow in microchannels. Fluid Dyn. Res. 40 (9), 679–694.CrossRefGoogle Scholar
Beskok, A. & Karniadakis, G. E. 1999 Report: a model for flows in channels, pipes, and ducts at micro and nano scales. Microscale Therm. Engng 3 (1), 43–77.Google Scholar
Bobylev, A. V. 1982 The Chapman–Enskog and Grad methods for solving the Boltzmann equation. Dokl. Akad. Nauk SSSR 27, 29–31.Google Scholar
Brenner, H. 2005 Navier–Stokes revisited. Physica A 349 (1), 60–132.Google Scholar
Cercignani, C. & Daneri, A. 1963 Flow of a rarefied gas between two parallel plates. J. Appl. Phys. 34 (12), 3509–3513.CrossRefGoogle Scholar
Chang, W. & Uhlenbeck, G. E.1948 On the transport phenomena in rarified gases. Tech Rep. DTIC Document.Google Scholar
Chapman, S. & Cowling, T. G. 1970 The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases. Cambridge University Press.Google Scholar
Comeaux, K. A., Chapman, D. R. & MacCormack, R. W.1995 An analysis of the Burnett equations based on the second law of thermodynamics. In Proceedings of the 33rd AIAA, Aerospace Sciences Meeting and Exhibit, Reno, NV. AIAA paper 95-0415.Google Scholar
Dadzie, S. K. 2013 A thermo-mechanically consistent Burnett regime continuum flow equation without Chapman–Enskog expansion. J. Fluid Mech. 716, R6.CrossRefGoogle Scholar
Dadzie, S. K. & Reese, J. M. 2012 Analysis of the thermomechanical inconsistency of some extended hydrodynamic models at high Knudsen number. Phys. Rev. E 85, 041202.Google Scholar
Dongari, N., Durst, F. & Chakraborty, S. 2010 Predicting microscale gas flows and rarefaction effects through extended Navier–Stokes–Fourier equations from phoretic transport considerations. Microfluid Nanofluid. 9 (4–5), 831–846.Google Scholar
Dongari, N., Sharma, A. & Durst, F. 2009 Pressure-driven diffusive gas flows in micro-channels: from the Knudsen to the continuum regimes. Microfluid. Nanofluid. 6 (5), 679–692.Google Scholar
Ewart, T., Perrier, P., Graur, I. A. & Meolans, J. G. 2007 Mass flow rate measurements in a microchannel, from hydrodynamic to near free molecular regimes. J. Fluid Mech. 584, 337–356.CrossRefGoogle Scholar
García-Colín, L. S., Velasco, R. M. & Uribe, F. J. 2008 Beyond the Navier–Stokes equations: Burnett hydrodynamics. Phys. Rep. 465 (4), 149–189.Google Scholar
Gatignol, R. 2012 Asymptotic modelling of flows in microchannel by using Navier–Stokes or Burnett equations and comparison with DSMC simulations. Vacuum 86 (12), 2014–2028.CrossRefGoogle Scholar
Grad, H. 1949 On the kinetic theory of rarefied gases. Commun. Pure Appl. Maths 2, 331–407.Google Scholar
Gu, X.-J. & Emerson, D. R. 2009 A high-order moment approach for capturing non-equilibrium phenomena in the transition regime. J. Fluid Mech. 636, 177–216.CrossRefGoogle Scholar
Jin, S. & Slemrod, M. 2001 Regularization of the Burnett equations via relaxation. J. Stat. Phys. 103 (5–6), 1009–1033.CrossRefGoogle Scholar
Karniadakis, G., Beskok, A. & Aluru, N. 2005 Microflows and Nanoflows: Fundamentals and Simulation. Springer.Google Scholar
Knudsen, M. 1909 Die Gesetze der Molekularströmung und der inneren Reibungsströmung der Gase durch Röhren. Ann. Phys. 333 (1), 75–130.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1958 Fluid Mechanics. Pergamon.Google Scholar
Pong, K., Ho, C. M., Liu, J. & Tai, Y. C. 1994 Non-linear pressure distribution in uniform microchannels. In Proceedings of Application of Microfabrication to Fluid Mechanics, ASME Winter Annual Meeting, Chicago, pp. 51–56.Google Scholar
Singh, N., Dongari, N. & Agrawal, A. 2014a Analytical solution of plane Poiseuille flow within burnett hydrodynamics. Microfluid Nanofluid. 16 (1–2), 403–412.Google Scholar
Singh, N., Gavasane, A. & Agrawal, A. 2014b Analytical solution of plane Couette flow in the transition regime and comparison with direct simulation Monte Carlo data. Comput. Fluids 97, 177–187.Google Scholar
Sreekanth, A. K. 1968 Slip flow through long circular tubes. In Rarefied Gas Dynamics (ed. Trilling, L. & Wachman, H. Y.). Academic Press.Google Scholar
Stevanovic, N. D. 2007 A new analytical solution of microchannel gas flow. J. Micromech. Microengng 17 (8), 1695–1702.Google Scholar
Struchtrup, H. & Torrilhon, M. 2003 Regularization of Grad’s 13 moment equations: derivation and linear analysis. Phys. Fluids 15, 2668–2680.Google Scholar
Tison, S. A. 1993 Experimental data and theoretical modeling of gas flows through metal capillary leaks. Vacuum 44 (11), 1171–1175.Google Scholar
Uribe, F. J. & Garcia, A. L. 1999 Burnett description for plane Poiseuille flow. Phys. Rev. E 60, 4063–4078.CrossRefGoogle ScholarPubMed
Varade, V., Agrawal, A. & Pradeep, A. M. 2014 Behaviour of rarefied gas flow near the junction of a suddenly expanding tube. J. Fluid Mech. 739, 363–391.CrossRefGoogle Scholar
Xue, H. & Ji, H. 2003 Prediction of flow and heat transfer characteristics in micro-Couette flow. Microscale Therm. Engng 7 (1), 51–68.CrossRefGoogle Scholar
Yang, Z. & Garimella, S. V. 2009 Rarefied gas flow in microtubes at different inlet–outlet pressure ratios. Phys. Fluids 21, 052005.CrossRefGoogle Scholar
Zhong, X.1991 Development and computation of continuum higher order constitutive relations for high-altitude hypersonic flow. PhD thesis, Stanford University.Google Scholar
Zhong, X. & Furumoto, G. H. 1995 Augmented Burnett-equation solutions over axisymmetric blunt bodies in hypersonic flow. J. Spacecr. Rockets 32 (4), 588–595.Google Scholar
Zohar, Y., Lee, S. Y. K., Lee, W. Y., Jiang, L. & Tong, P. 2002 Subsonic gas flow in a straight and uniform microchannel. J. Fluid Mech. 472, 125–151.Google Scholar