Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-28T16:38:52.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Breaking-onset, energy and momentum flux in unsteady focused wave packets

Published online by Cambridge University Press:  09 February 2016

Morteza Derakhti  and
James T. Kirby
Morteza Derakhti*
Affiliation:
Center for Applied Coastal Research, Department of Civil and Environmental Engineerings, University of Delaware, Newark, DE 19716, USA
James T. Kirby
Affiliation:
Center for Applied Coastal Research, Department of Civil and Environmental Engineerings, University of Delaware, Newark, DE 19716, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Breaking waves on the ocean surface transfer energy and momentum into currents and turbulence. What is less well understood, however, is the associated total loss of wave energy and momentum flux. Further, finding a robust and universal diagnostic parameter that determines the onset of breaking and its strength is still an open question. Derakhti & Kirby (J. Fluid Mech., vol. 761, 2014, pp. 464–506) have recently studied bubble entrainment and turbulence modulation by dispersed bubbles in isolated unsteady breaking waves using large-eddy simulation. In this paper, a new diagnostic parameter 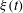${\it\xi}(t)$ is defined based on that originally proposed by Song & Banner (J. Phys. Oceanogr., vol. 32, 2002, pp. 2541–2558), and it is shown that using a threshold value of 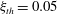${\it\xi}_{th}=0.05$, the new dynamic criteria is capable of detecting single and multiple breaking events in the considered packets. In addition, the spatial variation of the total energy and momentum flux in intermediate- and deep-water unsteady breaking waves generated by dispersive focusing is investigated. The accuracy of estimating these integral measures based on free surface measurements and using a characteristic wave group velocity is addressed. It is found that the new diagnostic parameter just before breaking, 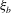${\it\xi}_{b}$, has a strong linear correlation with the commonly used breaking strength parameter 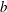$b$, suggesting that 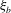${\it\xi}_{b}$ can be used to parameterize the averaged breaking-induced dissipation rate and its associated energy flux loss. It is found that the global wave packet time and length scales based on the spectrally weighted packet frequency proposed by Tian et al. (J. Fluid Mech., vol. 655, 2010, pp. 217–257), are the reasonable estimations of the time and length scales of the carrier wave in the packet close to the focal/break point. A global wave steepness, 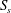$S_{s}$, is defined based on these spectrally weighted scales, and its spatial variation across the breaking region is examined. It is shown that the corresponding values of 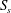$S_{s}$ far upstream of breaking, 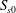$S_{s0}$, have a strong linear correlation with respect to 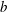$b$ for the considered focused wave packets. The linear relation, however, cannot provide accurate estimations of 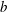$b$ in the range 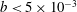$b<5\times 10^{-3}$. A new scaling law given by 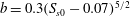$b=0.3(S_{s0}-0.07)^{5/2}$, which is consistent with inertial wave dissipation scaling of Drazen et al. (J. Fluid Mech., vol. 611, 2008, pp. 307–332), is shown to be capable of providing accurate estimates of 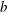$b$ in the full range of breaking intensities, where the scatter of data in the new formulation is significantly decreased compared with that proposed by Romero et al. (J. Phys. Oceanogr., vol. 42, 2012, pp. 1421–1444). Furthermore, we examine nonlinear interactions of different components in a focused wave packet, noting interactive effect on a characteristic wave group velocity in both non-breaking and breaking packets. Phase locking between spectral components is observed in the breaking region as well, and subsequently illustrated by calculating the wavelet bispectrum.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Turbulent Flows: Turbulence modelling Waves/Free-surface Flows: Wave breaking
Type
Papers
Information
Journal of Fluid Mechanics , Volume 790 , 10 March 2016 , pp. 553 - 581
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allis, M. J.2013 The speed, breaking onset and energy dissipation of 3d deep-water waves. PhD thesis, U. New South Wales.Google Scholar
Banner, M. L. & Peirson, W. L. 2007 Wave breaking onset and strength for two-dimensional deep-water wave groups. J. Fluid Mech. 585, 93–115.CrossRefGoogle Scholar
Banner, M. L. & Peregrine, D. H. 1993 Wave breaking in deep water. Annu. Rev. Fluid Mech. 25, 373–397.Google Scholar
Benjamin, T. B. & Feir, J. E. 1967 The disintegration of wave trains on deep water. Part 1. Theory. J. Fluid Mech. 27, 417–430.Google Scholar
Derakhti, M. & Kirby, J. T. 2014a Bubble entrainment and liquid-bubble interaction under unsteady breaking waves. J. Fluid Mech. 761, 464–506.Google Scholar
Derakhti, M. & Kirby, J. T.2014b Bubble entrainment and liquid-bubble interaction under unsteady breaking waves. Tech. Rep. CACR-14-06. Center for Applied Coastal Research, University of Delaware, available at http://www.udel.edu/kirby/papers/derakhti-kirby-cacr-14-06.pdf.Google Scholar
Drazen, D. A., Melville, W. K. & Lenain, L. 2008 Inertial scaling of dissipation in unsteady breaking waves. J. Fluid Mech. 611, 307–332.CrossRefGoogle Scholar
Duncan, J. H. 1983 The breaking and non-breaking wave resistance of a two-dimensional hydrofoil. J. Fluid Mech. 126, 507–520.CrossRefGoogle Scholar
Duncan, J. H. 2001 Spilling breakers. Annu. Rev. Fluid Mech. 33, 519–547.Google Scholar
Farge, M. 1992 Wavelet transforms and their applications to turbulence. Annu. Rev. Fluid Mech. 24, 395–458.Google Scholar
Gemmrich, J., Zappa, C. J., Banner, M. L. & Morison, R. P. 2013 Wave breaking in developing and mature seas. J. Geophys. Res. 118, 4542–4552.Google Scholar
Gemmrich, J. R., Banner, M. L. & Garrett, C. 2008 Spectrally resolved energy dissipation rate and momentum flux of breaking waves. J. Phys. Oceanogr. 38, 1296–1312.Google Scholar
Goullet, A. & Choi, W. 2011 Nonlinear evolution of irregular surface waves: comparison of numerical solutions with laboratory experiments for long crested waves. Phys. Fluids 23, 016601.Google Scholar
Grare, L., Peirson, W. L., Branger, H., Walker, J. W., Giovanangeli, J. & Makin, V. 2013 Growth and dissipation of wind-forced, deep-water waves. J. Fluid Mech. 722, 5–50.Google Scholar
Kiger, K. T. & Duncan, J. H. 2012 Air-entrainment mechanisms in plunging jets and breaking waves. Annu. Rev. Fluid Mech. 44, 563–596.Google Scholar
Melville, W. K. 1982 The instability and breaking of deep-water waves. J. Fluid Mech. 115, 165–185.Google Scholar
Melville, W. K. 1994 Energy dissipation by breaking waves. J. Phys. Oceanogr. 24, 2041–2049.Google Scholar
Melville, W. K. 1996 The role of surface-wave breaking in air–sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.Google Scholar
Perlin, M., Choi, W. & Tian, Z. 2013 Breaking waves in deep and intermediate waters. Annu. Rev. Fluid Mech. 45, 115–145.Google Scholar
Phillips, O. M., Posner, F. L. & Hansen, J. P. 2001 High range resolution radar measurements of the speed distribution of breaking events in wind-generated ocean waves: surface impulse and wave energy dissipation rates. J. Phys. Oceanogr. 31, 450–460.Google Scholar
Rapp, R. J. & Melville, W. K. 1990 Laboratory measurements of deep-water breaking waves. Phil. Trans. R. Soc. Lond. A 331, 735–800.Google Scholar
Romero, L., Melville, W. K. & Kleiss, J. M. 2012 Spectral energy dissipation due to surface wave breaking. J. Phys. Oceanogr. 42, 1421–1444.Google Scholar
Schwendeman, M., Thomson, J. & Gemmrich, J. R. 2014 Wave breaking dissipation in a young wind sea. J. Phys. Oceanogr. 44, 104–127.Google Scholar
Song, J. & Banner, M. L. 2002 On determining the onset and strength of breaking for deep water waves. Part I: unforced irrotational wave groups. J. Phys. Oceanogr. 32, 2541–2558.Google Scholar
Thomson, J., Gemmrich, J. R. & Jessup, A. T. 2009 Energy dissipation and the spectral distribution of whitecaps. Geophys. Res. Lett. 36, L11601.CrossRefGoogle Scholar
Tian, Z., Perlin, M. & Choi, W. 2008 Evaluation of a deep-water wave breaking criterion. Phys. Fluids 20, 066604.Google Scholar
Tian, Z., Perlin, M. & Choi, W. 2010 Energy dissipation in two-dimensional unsteady plunging breakers and an eddy viscosity model. J. Fluid Mech. 655, 217–257.Google Scholar
Tian, Z., Perlin, M. & Choi, W. 2012 An eddy viscosity model for two-dimensional breaking waves and its validation with laboratory experiments. Phys. Fluids 24, 036601.Google Scholar
Van Milligen, B. Ph., Hidalgo, C. & Sanchez, E. 1995 Nonlinear phenomena and intermittency in plasma turbulence. Phys. Rev. Lett. 74, 395–398.Google Scholar
West, B. J., Brueckner, K. A., Janda, R. S., Milder, D. M. & Milton, R. L. 1987 A new numerical method for surface hydrodynamics. J. Geophys. Res. 92, 11803–11824.Google Scholar
Wu, C. H & Nepf, H. M. 2002 Breaking criteria and energy losses for three-dimensional wave breaking. J. Geophys. Res. 107 (C10), 41,1–18.Google Scholar