Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T11:12:52.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Breakage, coalescence and size distribution of surfactant-laden droplets in turbulent flow

Published online by Cambridge University Press:  24 October 2019

Giovanni Soligo Open the ORCID record for Giovanni Soligo [Opens in a new window] ,
Alessio Roccon Open the ORCID record for Alessio Roccon [Opens in a new window]  and
Alfredo Soldati Open the ORCID record for Alfredo Soldati [Opens in a new window]
Giovanni Soligo
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, TU-Wien, 1060 Vienna, Austria Polytechnic Department, University of Udine, 33100 Udine, Italy
Alessio Roccon
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, TU-Wien, 1060 Vienna, Austria Polytechnic Department, University of Udine, 33100 Udine, Italy
Alfredo Soldati*
Affiliation:
Institute of Fluid Mechanics and Heat Transfer, TU-Wien, 1060 Vienna, Austria Polytechnic Department, University of Udine, 33100 Udine, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, we compute numerically breakage/coalescence rates and size distribution of surfactant-laden droplets in turbulent flow. We use direct numerical simulation of turbulence coupled with a two-order-parameter phase-field method to describe droplets and surfactant dynamics. We consider two different values of the surface tension (i.e. two values for the Weber number, 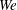$We$, the ratio between inertial and surface tension forces) and four types of surfactant (i.e. four values of the elasticity number, 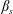$\unicode[STIX]{x1D6FD}_{s}$, which defines the strength of the surfactant). Stretching, breakage and merging of droplet interfaces are controlled by the complex interplay among shear stresses, surface tension and surfactant distribution, which are deeply intertwined. Shear stresses deform the interface, changing the local curvature and thus surface tension forces, but also advect surfactant over the interface. In turn, local increases of surfactant concentration reduce surface tension, changing the interface deformability and producing tangential (Marangoni) stresses. Finally, the interface feeds back to the local shear stresses via the capillary stresses, and changes the local surfactant distribution as it deforms, breaks and merges. We find that Marangoni stresses have a major role in restoring a uniform surfactant distribution over the interface, contrasting, in particular, the action of shear stresses: this restoring effect is proportional to the elasticity number and is stronger for smaller droplets. We also find that lower surface tension (higher 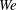$We$ or higher 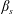$\unicode[STIX]{x1D6FD}_{s}$) increases the number of breakage events, as expected, but also the number of coalescence events, more unexpected. The increase of the number of coalescence events can be traced back to two main factors: the higher probability of inter-droplet collisions, favoured by the larger number of available droplets, and the decreased deformability of smaller droplets. Finally, we show that, for all investigated cases, the steady-state droplet size distribution is in good agreement with the 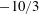$-10/3$ power-law scaling (Garrett et al., J. Phys. Oceanogr., vol. 30 (9), 2000, pp. 2163–2171), conforming to previous experimental observations (Deane & Stokes, Nature, vol. 418 (6900), 2002, p. 839) and numerical simulations (Skartlien et al., J. Chem. Phys., vol. 139 (17), 2013).

JFM classification

Drops and Bubbles: Breakup/coalescence Multiphase and Particle-laden Flows: Multiphase flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 881 , 25 December 2019 , pp. 244 - 282
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allan, R. S., Charles, G. E. & Mason, S. G. 1961 The approach of gas bubbles to a gas/liquid interface. J. Colloid Sci. 16 (2), 150–165.Google Scholar
Anderson, D. M., McFadden, G. B. & Wheeler, A. A. 1998 Diffuse interface methods in fluid mechanics. Annu. Rev. Fluid Mech. 30 (1), 139–165.Google Scholar
Aris, R. 1989 Vectors, Tensors and the Basic Equations of Fluid Mechanics. Dover Publications.Google Scholar
Babinsky, E. & Sojka, P. E. 2002 Modeling drop size distributions. Prog. Energy Combust. 28, 303–329.Google Scholar
Badalassi, V. E., Ceniceros, H. D. & Banerjee, S. 2003 Computation of multiphase systems with phase field models. J. Comput. Phys. 190 (2), 371–397.Google Scholar
Bazhlekov, I. B., Anderson, P. D. & Meijer, H. E. 2006 Numerical investigation of the effect of insoluble surfactants on drop deformation and breakup in simple shear flow. J. Colloid Interface Sci. 298 (1), 369–394.Google Scholar
Brown, D. E. & Pitt, K. 1972 Drop size distribution of stirred non-coalescing liquid–liquid system. Chem. Engng Sci. 27 (3), 577–583.Google Scholar
Brown, W. K. & Wohletz, K. H. 1995 Derivation of the Weibull distribution based on physical principles and its connection to the Rosin–Rammler and lognormal distributions. J. Appl. Phys. 78 (4), 2758–2763.Google Scholar
Cahn, J. W. & Hilliard, J. E. 1958 Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 28, 258–267.Google Scholar
Cahn, J. W. & Hilliard, J. E. 1959a Free energy of a nonuniform system. II. Thermodynamic basis. J. Chem. Phys. 30 (5), 1121–1124.Google Scholar
Cahn, J. W. & Hilliard, J. E. 1959b Free energy of a nonuniform system. III. Nucleation in a two-component incompressible fluid. J. Chem. Phys. 31, 688–699.Google Scholar
Calabrese, R. V., Wang, C. Y. & Bryner, N. P. 1986 Drop breakup in turbulent stirred-tank contactors. Part III: correlations for mean size and drop size distribution. AIChE J. 32 (4), 677–681.Google Scholar
Canuto, C., Hussaini, M. Y., Quarteroni, A. M. & Zang, T. A. 1988 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Chang, C. & Franses, E. 1995 Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloids Surf. A 100, 1–45.Google Scholar
Charles, G. E. & Mason, S. G. 1960 The coalescence of liquid drops with flat liquid/liquid interfaces. J. Colloid Sci. 15 (3), 236–267.Google Scholar
Chatzi, E. G. & Kiparissides, C. 1994 Drop size distributions in high holdup fraction dispersion systems: effect of the degree of hydrolysis of PVA stabilizer. Chem. Engng Sci. 49 (24), 5039–5052.Google Scholar
Chen, H. T. & Middleman, S. 1967 Drop size distribution in agitated liquid–liquid systems. AIChE J. 13 (5), 989–995.Google Scholar
Chen, N., Kuhl, T., Tadmor, R., Lin, Q. & Israelachvili, J. 2004 Large deformations during the coalescence of fluid interfaces. Phys. Rev. Lett. 92, 024501.Google Scholar
Chen, S. & Doolen, G. D. 1998 Lattice Boltzmann method for fluid flows. Annu. Rev. Fluid Mech. 30 (1), 329–364.Google Scholar
Colella, D., Vinci, D., Bagatin, R., Masi, M. & Bakr, E. A. 1999 A study on coalescence and breakage mechanisms in three different bubble columns. Chem. Engng Sci. 54 (21), 4767–4777.Google Scholar
Dai, B. & Leal, L. G. 2008 The mechanism of surfactant effects on drop coalescence. Phys. Fluids 20 (4), 1–13.Google Scholar
Deane, G. B. & Stokes, M. D. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418 (6900), 839.Google Scholar
Deike, L., Melville, W. K. & Popinet, S. 2016 Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 801, 91–129.Google Scholar
Delhaye, J. M. & Bricard, P. 1994 Interfacial area in bubbly flow: experimental data and correlations. Nucl. Engng Des. 151 (1), 65–77.Google Scholar
Dodd, M. S. & Ferrante, A. 2016 On the interaction of Taylor length scale size droplets and isotropic turbulence. J. Fluid Mech. 806, 356–412.Google Scholar
Eastwood, C. D., Armi, L. & Lasheras, J. C. 2004 The breakup of immiscible fluids in turbulent flows. J. Fluid Mech. 502, 309–333.Google Scholar
Eggers, J. 1995 Theory of drop formation. Phys. Fluids 7 (5), 941–953.Google Scholar
Eggleton, C. D., Tsai, T. M. & Stebe, K. J. 2001 Tip streaming from a drop in the presence of surfactants. Phys. Rev. Lett. 87 (4), 048302.Google Scholar
Elfring, G. J., Leal, L. G. & Squires, T. M. 2016 Surface viscosity and marangoni stresses at surfactant laden interfaces. J. Fluid Mech. 792, 712–739.Google Scholar
Elghobashi, S. 2019 Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 51 (1), 217–244.Google Scholar
Engblom, S., Do-Quang, M., Amberg, G. & Tornberg, A. K. 2013 On diffuse interface modeling and simulation of surfactants in two-phase fluid flow. Commun. Comput. Phys. 14 (4), 879–915.Google Scholar
Farhat, H., Celiker, F., Singh, T. & Lee, J. S. 2011 A hybrid lattice Boltzmann model for surfactant-covered droplets. Soft Matt. 7 (5), 1968–1985.Google Scholar
Fedkiw, R. P., Aslam, T., Merriman, B. & Osher, S. 1999 A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152 (2), 457–492.Google Scholar
Garrett, C., Li, M. & Farmer, D. 2000 The connection between bubble size spectra and energy dissipation rates in the upper ocean. J. Phys. Oceanogr. 30 (9), 2163–2171.Google Scholar
Gibou, F., Fedkiw, R. & Osher, S. 2018 A review of level-set methods and some recent applications. J. Comput. Phys. 353, 82–109.Google Scholar
He, X., Chen, S. & Zhang, R. 1999 A lattice Boltzmann scheme for incompressible multiphase flow and its application in simulation of Rayleigh–Taylor instability. J. Comput. Phys. 152 (2), 642–663.Google Scholar
Herrmann, M. 2011 On simulating primary atomization using the refined level set grid method. Atomiz. Spray 21, 283–301.Google Scholar
Hinze, J. O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1 (3), 289–295.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.Google Scholar
Hsu, C. T., Chang, C. H. & Lin, S. Y. 2000 Study on surfactant adsorption kinetics: effects of interfacial curvature and molecular interaction. Langmuir 16 (3), 1211–1215.Google Scholar
Hussaini, M. Y. & Zang, T. A. 1987 Spectral methods in fluid dynamics. Annu. Rev. Fluid Mech. 19 (1), 339–367.Google Scholar
Jacqmin, D. 1999 Calculation of two-phase Navier–Stokes flows using phase-field modeling. J. Comput. Phys. 155 (1), 96–127.Google Scholar
James, A. J. & Lowengrub, J. 2004 A surfactant-conserving volume-of-fluid method for interfacial flows with insoluble surfactant. J. Comput. Phys. 201 (2), 685–722.Google Scholar
Ju, H., Jiang, Y., Geng, T., Wang, Y. & Zhang, C. 2017 Equilibrium and dynamic surface tension of quaternary ammonium salts with different hydrocarbon chain length of counterions. J. Mol. Liq. 225, 606–612.Google Scholar
Kamat, P. M., Wagoner, B. W., Thete, S. S. & Basaran, O. A. 2018 Role of Marangoni stress during breakup of surfactant-covered liquid threads: reduced rates of thinning and microthread cascades. Phys. Rev. Fluids 3, 043602.Google Scholar
Kamp, J., Villwock, J. & Kraume, M. 2017 Drop coalescence in technical liquid/liquid applications: a review on experimental techniques and modeling approaches. Rev. Chem. Engng 33 (1), 1–47.Google Scholar
Karabelas, A. J. 1978 Droplet size spectra generated in turbulent pipe flow of dilute liquid/liquid dispersions. AIChE J. 24 (2), 170–180.Google Scholar
Kelly, J. E. & Kazimi, M. S. 1982 Interfacial exchange relations for two-fluid vapor–liquid flow: a simplified regime-map approach. Nucl. Sci. Engng 81 (3), 305–318.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low Reynolds number. J. Fluid Mech. 177 (1), 133–166.Google Scholar
Kiyomi, A. & Fumitake, Y. 1974 Bubble size, interfacial area, and liquid-phase mass transfer coefficient in bubble columns. Ind. Engng Chem. Process Des. Dev. 13 (1), 84–91.Google Scholar
Komura, S. & Kodama, H. 1997 Two-order-parameter model for an oil-water-surfactant system. Phys. Rev. E 55 (2), 1722–1727.Google Scholar
Korteweg, D. J. 1901 Sur la forme que prennent les equations du mouvements des fluides si l’on tient compte des forces capillaires causées par des variations de densité considérables mais continues et sur la théorie de la capillarité dans l’hypothèse d’une variation continue de la densité (in French). Arch. Néerlandaises Sci. Exactes et Naturelles 6, 1–24.Google Scholar
Kralova, I. & Sjöblom, J. 2009 Surfactants used in food industry: a review. J. Disper. Sci. Technol. 30 (9), 1363–1383.Google Scholar
Kwakkel, M., Breugem, W.-P. & Boersma, B. J. 2013 Extension of a CLSVOF method for droplet-laden flows with a coalescence/breakup model. J. Comput. Phys. 253, 166–188.Google Scholar
Lai, M. C., Tseng, Y. H. & Huang, H. 2008 An immersed boundary method for interfacial flows with insoluble surfactant. J. Comput. Phys. 227 (15), 7279–7293.Google Scholar
Lai, M. C., Tseng, Y. H. & Huang, H. 2010 Numerical simulation of moving contact lines with surfactant by immersed boundary method. Commun. Comput. Phys. 8 (4), 735.Google Scholar
Langevin, D. 2014 Rheology of adsorbed surfactant monolayers at fluid surfaces. Annu. Rev. Fluid Mech. 46, 47–65.Google Scholar
Laradji, M., Guo, H., Grant, M. & Zuckermann, M. J. 1992 The effect of surfactants on the dynamics of phase separation. J. Phys.: Condens. Matter 4, 6715–6728.Google Scholar
Lasheras, J. C., Eastwood, C., Martınez-Bazán, C. & Montanes, J. L. 2002 A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Intl J. Multiphase Flow 28 (2), 247–278.Google Scholar
Lee, T. W. & Robinson, D. 2011 Calculation of the drop size distribution and velocities from the integral form of the conservation equations. Combust. Sci. Technol. 183, 271–284.Google Scholar
Li, Y., Choi, J. & Kim, J. 2016 A phase-field fluid modeling and computation with interfacial profile correction term. Commun. Nonlinear Sci. 30 (1-3), 84–100.Google Scholar
Liao, Y. & Lucas, D. 2010 A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Engng Sci. 65, 2851–2864.Google Scholar
Liu, H., Ba, Y., Wu, L., Li, Z., Xi, G. & Zhang, Y. 2018 A hybrid lattice Boltzmann and finite difference method for droplet dynamics with insoluble surfactants. J. Fluid Mech. 837, 381–412.Google Scholar
López-Díaz, D., García-Mateos, I. & Velázquez, M. M. 2006 Surface properties of mixed monolayers of sulfobetaines and ionic surfactants. J. Colloid Interface Sci. 299 (2), 858–866.Google Scholar
Lovick, J., Mouza, A. A., Paras, S. V., Lye, G. J. & Angeli, P. 2005 Drop size distribution in highly concentrated liquid–liquid dispersions using a light back scattering method. J. Chem. Technol. Biotechnol. 80 (5), 545–552.Google Scholar
Lu, J., Muradoglu, M. & Tryggvason, G. 2017 Effect of insoluble surfactant on turbulent bubbly flows in vertical channels. Intl J. Multiphase Flow 95, 135–143.Google Scholar
Lu, J. & Tryggvason, G. 2008 Effect of bubble deformability in turbulent bubbly upflow in a vertical channel. Phys. Fluids 20 (4), 040701.Google Scholar
Lu, J. & Tryggvason, G. 2018 Direct numerical simulations of multifluid flows in a vertical channel undergoing topology changes. Phys. Rev. Fluids 3, 084401.Google Scholar
Lu, J. & Tryggvason, G. 2019 Multifluid flows in a vertical channel undergoing topology changes: effect of void fraction. Phys. Rev. Fluids 4, 084301.Google Scholar
Luo, H. & Svendsen, H. F. 1996 Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 42 (5), 1225–1233.Google Scholar
Magaletti, F., Picano, F., Chinappi, M., Marino, L. & Casciola, C. M. 2013 The sharp-interface limit of the Cahn–Hilliard/Navier–Stokes model for binary fluids. J. Fluid Mech. 714, 95–126.Google Scholar
Mugele, R. A. & Evans, H. D. 1951 Droplet size distribution in sprays. Ind. Engng Chem. Res. 43 (6), 1317–1324.Google Scholar
Muradoglu, M. & Tryggvason, G. 2014 Simulations of soluble surfactants in 3D multiphase flow. J. Comput. Phys. 274, 737–757.Google Scholar
Notz, P. K. & Basaran, O. A. 2004 Dynamics and breakup of a contracting liquid filament. J. Fluid Mech. 512, 223–256.Google Scholar
Pereira, R., Ashton, I., Sabbaghzadeh, B., Shutler, J. D. & Upstill-Goddard, R. C. 2018 Reduced air–sea CO2 exchange in the Atlantic Ocean due to biological surfactants. Nat. Geosci. 11, 492–496.Google Scholar
Perlekar, P., Biferale, L. & Sbragaglia, M. 2012 Droplet size distribution in homogeneous isotropic turbulence. Phys. Fluids 065101, 1–10.Google Scholar
Peyret, R. 2002 Spectral Methods for Incompressible Viscous Flow. Springer.Google Scholar
Piedfert, A., Lalanne, B., Masbernat, O. & Risso, F. 2018 Numerical simulations of a rising drop with shape oscillations in the presence of surfactants. Phys. Rev. Fluids 3, 103605.Google Scholar
Popinet, S. 2018 Numerical models of surface tension. Annu. Rev. Fluid Mech. 50, 1–28.Google Scholar
Porter, M. R. 1991 Handbook of Surfactants. Springer.Google Scholar
Rekvig, L. & Frenkel, D. 2007 Molecular simulations of droplet coalescence in oil/water/surfactant systems. J. Chem. Phys. 127 (13), 134701.Google Scholar
Renardy, Y., Renardy, M. & Cristini, V. 2002 A new volume-of-fluid formulation for surfactants and simulations of drop deformation under shear at a low viscosity ratio. Eur. J. Mech. (B/Fluid) 21 (1), 49–59.Google Scholar
Roccon, A., De Paoli, M., Zonta, F. & Soldati, A. 2017 Viscosity-modulated breakup and coalescence of large drops in bounded turbulence. Phys. Rev. Fluids 2, 083603.Google Scholar
Roccon, A., Zonta, F. & Soldati, A. 2019 Turbulent drag reduction by compliant lubricating layer. J. Fluid Mech. 863, R1.Google Scholar
Rosen, M. J. & Kunjappu, J. T. 2012 Surfactants and Interfacial Phenomena. Wiley.Google Scholar
Rosti, M. E., De Vita, F. & Brandt, L. 2019a Numerical simulations of emulsions in shear flows. Acta Mech. 230, 667–682.Google Scholar
Rosti, M. E., Ge, Z., Jain, S. S., Dodd, M. S. & Brandt, L. 2019b Droplets in homogeneous shear turbulence. J. Fluid Mech. 876, 962–984.Google Scholar
Scarbolo, L., Bianco, F. & Soldati, A. 2015 Coalescence and breakup of large droplets in turbulent channel flow. Phys. Fluids 27 (7), 073302.Google Scholar
Scarbolo, L., Bianco, F. & Soldati, A. 2016 Turbulence modification by dispersion of large deformable droplets. Eur. J. Mech. (B/Fluid) 55, 294–299.Google Scholar
Scarbolo, L., Molin, D., Perlekar, P., Sbragaglia, M., Soldati, A. & Toschi, F. 2013 Unified framework for a side-by-side comparison of different multicomponent algorithms: Lattice Boltzmann versus phase field model. J. Comput. Phys. 234, 263–279.Google Scholar
Scardovelli, R. & Zaleski, S. 1999 Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 31 (1), 567–603.Google Scholar
Sethian, J. A. 1999 Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science, vol. 3. Cambridge University Press.Google Scholar
Shan, X. & Chen, H. 1993 Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 47 (3), 1815.Google Scholar
Skartlien, R., Sollum, E. & Schumann, H. 2013 Droplet size distributions in turbulent emulsions: breakup criteria and surfactant effects from direct numerical simulations. J. Chem. Phys. 139 (17), 174901.Google Scholar
Soldati, A. & Banerjee, S. 1998 Turbulence modification by large-scale organized electrohydrodynamic flows. Phys. Fluids 10 (7), 1742–1756.Google Scholar
Soligo, G., Roccon, A. & Soldati, A. 2019a Coalescence of surfactant-laden drops by phase field method. J. Comput. Phys. 376, 1292–1311.Google Scholar
Soligo, G., Roccon, A. & Soldati, A. 2019b Mass conservation improved phase field methods for turbulent multiphase flow simulation. Acta Mech. 230, 683–696.Google Scholar
Speziale, C. G. 1987 On the advantages of the vorticity–velocity formulation of the equations of fluid dynamics. J. Comput. Phys. 73 (2), 476–480.Google Scholar
Sreehari, P., Borg, M. K., Chubynsky, M. V., Sprittles, J. E. & Reese, J. M. 2019 Droplet coalescence is initiated by thermal motion. Phys. Rev. Lett. 122 (10), 104501.Google Scholar
Stone, H. A. & Leal, L. G. 1990 The effects of surfactants on drop deformation and breakup. J. Fluid Mech. 220, 161–186.Google Scholar
Sun, Y. & Beckermann, C. 2007 Sharp interface tracking using the phase-field equation. J. Comput. Phys. 220 (2), 626–653.Google Scholar
Takagi, S. & Matsumoto, Y. 2011 Surfactant effects on bubble motion and bubbly flows. Annu. Rev. Fluid Mech. 43, 615–636.Google Scholar
Than, P., Preziosi, L., Joseph, D. D. & Arney, M. 1988 Measurement of interfacial tension between immiscible liquids with the spinning rod tensiometer. J. Colloid Interface Sci. 124 (2), 552–559.Google Scholar
Tryggvason, G., Bunner, B., Esmaeeli, A., Juric, D., Tauber, W., Han, J., Nas, S. & Jan, Y. 2001 A front-tracking method for the computations of multiphase flow. J. Comput. Phys. 759, 708–759.Google Scholar
Tryggvason, G., Scardovelli, R. & Zaleski, S. 2011 Direct Numerical Simulations of Gas–Liquid Multiphase Flows. Cambridge University Press.Google Scholar
Tsouris, C. & Tavlarides, L. L. 1994 Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 40 (3), 395–406.Google Scholar
Valentas, K. J. & Amundson, N. R. 1966 Breakage and coalescence in dispersed phase systems. Ind. Engng Chem. Fundam. 5 (4), 533–542.Google Scholar
van der Waals, J. D. 1979 The thermodynamic theory of capillarity under the hypothesis of a continuous variation of density. J. Stat. Phys. 20, 200–244.Google Scholar
Weinheimer, R. M., Fennell, D. E. & Cussler, E. L. 1981 Diffusion in surfactant solutions. J. Colloid Interface Sci. 80 (2), 357–368.Google Scholar
Xu, J. J., Li, Z., Lowengrub, J. & Zhao, H. 2011 Numerical study of surfactant-laden drop–drop interactions. Commun. Comput. Phys. 10 (2), 453–473.Google Scholar
Xu, J. J. & Zhao, H. K. 2003 An Eulerian formulation for solving partial differential equations along a moving interface. SIAM J. Sci. Comput. 19 (1), 573–594.Google Scholar
Xu, J. J., Zhilin, L., Lowengrub, J. & Zhao, H. 2006 A level-set method for interfacial flows with surfactant. J. Comput. Phys. 212, 590–616.Google Scholar
Yue, P., Feng, J. J., Liu, C. & Shen, J. 2004 A diffuse-interface method for simulating two-phase flows of complex fluids. J. Fluid Mech. 515 (1), 293–317.Google Scholar
Yue, P., Zhou, C. & Feng, J. J. 2007 Spontaneous shrinkage of drops and mass conservation in phase-field simulations. J. Comput. Phys. 223 (1), 1–9.Google Scholar
Yue, P., Zhou, C. & Feng, J. J. 2010 Sharp-interface limit of the Cahn–Hilliard model for moving contact lines. J. Fluid Mech. 645 (8), 279.Google Scholar
Yun, A., Li, Y. & Kim, J. 2014 A new phase-field model for a water-oil-surfactant system. Appl. Math. Comput. 229, 422–432.Google Scholar
Zhang, Y. & Ye, W. 2017 A flux-corrected phase-field method for surface diffusion. Commun. Comput. Phys. 22 (2), 422–440.Google Scholar