Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-02T19:30:08.051Z Has data issue: false hasContentIssue false
  • English
  • Français

Bistability in the rotational motion of rigid and flexible flyers

Published online by Cambridge University Press:  26 June 2018

Yangyang Huang ,
Leif Ristroph ,
Mitul Luhar Open the ORCID record for Mitul Luhar [Opens in a new window]  and
Eva Kanso Open the ORCID record for Eva Kanso [Opens in a new window]
Yangyang Huang
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Leif Ristroph
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA
Mitul Luhar
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
Eva Kanso*
Affiliation:
Aerospace and Mechanical Engineering, University of Southern California, Los Angeles, CA 90089, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We explore the rotational stability of hovering flight in an idealized two-dimensional model. Our model is motivated by an experimental pyramid-shaped object (Weathers et al., J. Fluid Mech, vol. 650, 2010, pp. 415–425; Liu et al., Phys. Rev. Lett., vol. 108, 2012, 068103) and a computational 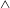$\wedge$-shaped analogue (Huang et al., Phys. Fluids, vol. 27 (6), 2015, 061706; Huang et al., J. Fluid Mech., vol. 804, 2016, pp. 531–549) hovering passively in oscillating airflows; both systems have been shown to maintain rotational balance during free flight. Here, we attach the 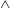$\wedge$-shaped flyer at its apex in oscillating flow, allowing it to rotate freely akin to a pendulum. We use computational vortex sheet methods and we develop a quasi-steady point-force model to analyse the rotational dynamics of the flyer. 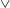We find that the flyer exhibits stable concave-down ($\wedge$) and concave-up ($\vee$) behaviour. Importantly, the down and up configurations are bistable and co-exist for a range of background flow properties. We explain the aerodynamic origin of this bistability and compare it to the inertia-induced stability of an inverted pendulum oscillating at its base. We then allow the flyer to flap passively by introducing a rotational spring at its apex. For stiff springs, flexibility diminishes upward stability but as stiffness decreases, a new transition to upward stability is induced by flapping. We conclude by commenting on the implications of these findings for biological and man-made aircraft.

JFM classification

Aerodynamics: Aerodynamics Aerodynamics: Flow-structure interactions Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 849 , 25 August 2018 , pp. 1043 - 1067
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alben, S. 2009 Simulating the dynamics of flexible bodies and vortex sheets. J. Comput. Phys. 228 (7), 2587–2603.Google Scholar
Alben, S. 2010 Flexible sheets falling in an inviscid fluid. Phys. Fluids 22 (6), 061901.Google Scholar
Butikov, E. I. 2001 On the dynamic stabilization of an inverted pendulum. Am. J. Phys. 69 (7), 755–768.Google Scholar
Chen, Y., Wang, H., Helbling, E. F., Jafferis, N. T., Zufferey, R., Ong, A., Ma, K., Gravish, N., Chirarattananon, P., Kovac, M. & Wood, R. J. 2017 A biologically inspired, flapping-wing, hybrid aerial-aquatic microrobot. Sci. Robot. 2 (11), 1–11.Google Scholar
Childress, S., Vandenberghe, N. & Zhang, J. 2006 Hovering of a passive body in an oscillating airflow. Phys. Fluids 18 (11), 117103.Google Scholar
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.Google Scholar
Ellington, C. P. 1985 Power and efficiency of insect flight muscle. J. Expl Biol. 115 (1), 293–304.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.Google Scholar
Fang, F., Ho, K. L., Ristroph, L. & Shelley, M. J. 2017 A computational model of the flight dynamics and aerodynamics of a jellyfish-like flying machine. J. Fluid Mech. 819, 621–655.Google Scholar
Feldman, A. G. & Levin, M. F. 2009 Progress in Motor Control, vol. 629. Springer.Google Scholar
Fry, S. N., Sayaman, R. & Dickinson, M. H. 2003 The aerodynamics of free-flight maneuvers in drosophila. Science 300 (5618), 495–498.Google Scholar
Graule, M. A., Chirarattananon, P., Fuller, S. B., Jafferis, N. T., Ma, K. Y., Spenko, M., Kornbluh, R. & Wood, R. J. 2016 Perching and takeoff of a robotic insect on overhangs using switchable electrostatic adhesion. Science 352 (6288), 978–982.Google Scholar
Huang, Y. & Kanso, E. 2015 Periodic and chaotic flapping of insectile wings. Eur. Phys. J. Special Topics 224 (17–18), 3175–3183.Google Scholar
Huang, Y., Nitsche, M. & Kanso, E. 2015 Stability versus maneuverability in hovering flight. Phys. Fluids 27 (6), 061706.Google Scholar
Huang, Y., Nitsche, M. & Kanso, E. 2016 Hovering in oscillatory flows. J. Fluid Mech. 804, 531–549.Google Scholar
Jones, M. A. 2003 The separated flow of an inviscid fluid around a moving flat plate. J. Fluid Mech. 496, 405–441.Google Scholar
Jones, M. A. & Shelley, M. J. 2005 Falling cards. J. Fluid Mech. 540, 393–425.Google Scholar
Keulegan, H. & Carpenter, L. H. 1958 Forces on cylinders and plates in an oscillating fluid. J. Res. Natl Bur. Stand. 60 (1), 423–440.Google Scholar
Krasny, R. 1986 Desingularization of periodic vortex sheet roll-up. J. Comput. Phys. 65 (2), 292–313.Google Scholar
Liu, B., Ristroph, L., Weathers, A., Childress, S. & Zhang, J. 2012 Intrinsic stability of a body hovering in an oscillating airflow. Phys. Rev. Lett. 108, 068103.Google Scholar
Ma, K. Y., Chirarattananon, P., Fuller, S. B. & Wood, R. J. 2013 Controlled flight of a biologically inspired, insect-scale robot. Science 340 (6132), 603–607.Google Scholar
Nitsche, M. & Krasny, R. 1994 A numerical study of vortex ring formation at the edge of a circular tube. J. Fluid Mech. 276, 139–161.Google Scholar
Pringle, J. W. S. 2003 Insect Flight, vol. 9. Cambridge University Press.Google Scholar
Ristroph, L., Bergou, A. J., Ristroph, G., Coumes, K., Berman, G. J., Guckenheimer, J., Wang, Z. J. & Cohen, I. 2010 Discovering the flight autostabilizer of fruit flies by inducing aerial stumbles. Proc. Natl Acad. Sci. USA 107 (11), 4820–4824.Google Scholar
Ristroph, L. & Childress, S. 2014 Stable hovering of a jellyfish-like flying machine. J. R. Soc. Interface 11 (92), 20130992.Google Scholar
Sane, S. P. 2003 The aerodynamics of insect flight. J. Expl Biol. 206 (23), 4191–4208.Google Scholar
Sheng, J. X., Ysasi, A., Kolomenskiy, D., Kanso, E., Nitsche, M. & Schneider, K. 2012 Simulating vortex wakes of flapping plates. In Natural Locomotion in Fluids and on Surfaces (ed. Childress, S., Hosoi, A., Schultz, W. W. & Wang, J.), pp. 255–262. Springer.Google Scholar
Shukla, R. K. & Eldredge, J. D. 2007 An inviscid model for vortex shedding from a deforming body. Theor. Comput. Fluid Dyn. 21 (5), 343–368.Google Scholar
Spedding, G. R., Rosén, M. & Hedenström, A. 2003 A family of vortex wakes generated by a thrush nightingale in free flight in a wind tunnel over its entire natural range of flight speeds. J. Expl Biol. 206 (14), 2313–2344.Google Scholar
Sun, M. 2014 Insect flight dynamics: stability and control. Rev. Mod. Phys. 86, 615–646.Google Scholar
Taylor, G. K. & Krapp, H. G. 2007 Sensory systems and flight stability: what do insects measure and why? Adv. Insect Physiol. 34, 231–316.Google Scholar
Thomas, A. L. R., Taylor, G. K., Srygley, R. B., Nudds, R. L. & Bomphrey, R. J. 2004 Dragonfly flight: free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Expl Biol. 207 (24), 4299–4323.Google Scholar
Vogel, S. 2009 Glimpses of Creatures in Their Physical Worlds. Princeton University Press.Google Scholar
Wang, Z. J. 2005 Dissecting insect flight. Annu. Rev. Fluid Mech. 37 (1), 183–210.Google Scholar
Wang, Z. J., Birch, J. M. & Dickinson, M. H. 2004 Unsteady forces and flows in low Reynolds number hovering flight: two-dimensional computations vs robotic wing experiments. J. Expl Biol. 207 (3), 449–460.Google Scholar
Warrick, D. R., Tobalske, B. W. & Powers, D. R. 2005 Aerodynamics of the hovering hummingbird. Nature 435 (7045), 1094–1097.Google Scholar
Weathers, A., Folie, B., Liu, B., Childress, S. & Zhang, J. 2010 Hovering of a rigid pyramid in an oscillatory airflow. J. Fluid Mech. 650, 415–425.Google Scholar
Wright, O. & Wright, W.1906 Flying-machine. US Patent 821 393.Google Scholar