Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T16:25:21.981Z Has data issue: false hasContentIssue false
  • English
  • Français

Bistability and hysteresis of axisymmetric thermal convection between differentially rotating spheres

Published online by Cambridge University Press:  25 January 2021

P.M. Mannix Open the ORCID record for P.M. Mannix [Opens in a new window]  and
A.J. Mestel Open the ORCID record for A.J. Mestel [Opens in a new window]
P.M. Mannix*
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
A.J. Mestel
Affiliation:
Department of Mathematics, Imperial College London, LondonSW7 2AZ, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

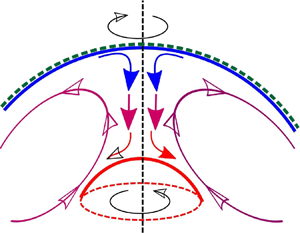
Heating a quiescent fluid from below gives rise to cellular convective motion as the temperature gradient becomes sufficiently steep. Typically, this transition increases heat transfer. Differentially rotating spherical shells also generate a state of cellular motion, which in this case transports angular momentum. When both effects are present, it is often assumed that the fluid adopts a configuration which maximises the transfer of angular momentum and heat. Depending on how the equilibrium is reached, however, this maximisation may not always be achieved, with two different stable equilibria often co-existing for the same heating and rotation strengths. We want to understand why the fluid motion in a spherical shell is bistable, and how this scenario might arise. We consider a deep, highly viscous fluid layer, of relevance to the ice shells of Saturn's and Jupiter's moons. We find that bistability depends largely on the relative strength of heating and differential rotation, as characterised by the Rayleigh number $Ra$ and inner sphere Reynolds number $Re_1$, and that the nature of the transition between bistable states depends strongly on the ratio of momentum diffusivity $\nu$ to thermal diffusivity $\kappa$ defined by the Prandtl number ${\textit {Pr}} = \nu /\kappa$. In particular, we find that the transition between solutions at large ${\textit {Pr}}$, depends on the strength of thin thermal layers and can occur either due to the destabilisation of an equatorial jet by buoyancy forces, or alternatively of a polar thermal plume by differential rotation. Our results demonstrate that, although bistability in this system cannot be simply explained by the flow maximising its torque or heat transfer, the polar and equatorial regions are of particular significance.

JFM classification

Convection: Convection Nonlinear Dynamical Systems: Nonlinear Dynamical Systems Instability: Instability
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 911 , 25 March 2021 , A12
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Araki, K., Yanase, S. & Mizushima, J. 1996 Symmetry breaking by differential rotation and saddle-node bifurcation of the thermal convection in a spherical shell. J. Phys. Soc. Japan 65 (12), 3862–3870.CrossRefGoogle Scholar
Barr, A.C. & McKinnon, W.B. 2007 Convection in Enceladus’ ice shell: conditions for initiation. Geophys. Res. Lett. 34 (9), L09202.CrossRefGoogle Scholar
Bühler, K. 1990 Symmetric and asymmetric Taylor vortex flow in spherical gaps. Acta Mech. 81 (1), 3–38.CrossRefGoogle Scholar
Crawford, J.D. & Knobloch, E. 1991 Symmetry and symmetry-breaking bifurcations in fluid dynamics. Annu. Rev. Fluid Mech. 23 (1), 341–387.CrossRefGoogle Scholar
Feudel, F., Bergemann, K., Tuckerman, L.S., Egbers, C., Futterer, B., Gellert, M. & Hollerbach, R. 2011 Convection patterns in a spherical fluid shell. Phys. Rev. E 83, 046304.CrossRefGoogle Scholar
Feudel, U., Pisarchik, A.N. & Showalter, K. 2018 Multistability and tipping: from mathematics and physics to climate and brain–minireview and preface to the focus issue. Chaos 28 (3), 033501.CrossRefGoogle ScholarPubMed
Goldstein, H.F., Knobloch, E., Mercader, I. & Net, M. 1993 Convection in a rotating cylinder. Part 1. Linear theory for moderate Prandtl numbers. J. Fluid Mech. 248, 583–604.CrossRefGoogle Scholar
Golubitsky, M. & Schaeffer, D. 1985 Singularities and Groups in Bifurcation Theory. Applied Mathematical Sciences, vol. 1. Springer.CrossRefGoogle Scholar
Hollerbach, R., Junk, M. & Egbers, C. 2006 Non-axisymmetric instabilities in basic state spherical Couette flow. Fluid Dyn. Res. 38 (4), 257–273.CrossRefGoogle Scholar
Huisman, S., van der Veen, R., Sun, C. & Lohse, D. 2014 Multiple states in highly turbulent Taylor–Couette flow. Nat. Commun. 5, 3820.CrossRefGoogle ScholarPubMed
Inagaki, T., Itano, T. & Sugihara-Seki, M. 2019 Numerical study on the axisymmetric state in spherical Couette flow under unstable thermal stratification. Acta Mech. 230 (10), 3499–3509.CrossRefGoogle Scholar
Jensen, H.J. 1998 Self-Organized Criticality: Emergent Complex Behavior in Physical and Biological Systems, vol. 10. Cambridge University Press.CrossRefGoogle Scholar
Johansson, H.T. & Forssén, C. 2016 Fast and accurate evaluation of Wigner 3 j, 6 j, and 9 j symbols using prime factorization and multiword integer arithmetic. SIAM J. Sci. Comput. 38 (1), A376–A384.CrossRefGoogle Scholar
Junk, M. & Egbers, C. 2000 Isothermal spherical Couette flow. In Physics of Rotating Fluids (ed. C. Egbers & G. Pfister), pp. 215–233. Springer.CrossRefGoogle Scholar
Knobloch, E. 1994 Bifurcations in Rotating Systems, pp. 331–372. Cambridge University Press.Google Scholar
Knobloch, E., Moore, D.R., Toomre, J. & Weiss, N.O. 1986 Transitions to chaos in two-dimensional double-diffusive convection. J. Fluid Mech. 166, 409–448.CrossRefGoogle Scholar
Kuznetsov, Y.A. 2004 Elements of Applied Bifurcation Theory. Applied Mathematical Science, vol. 112. Springer.CrossRefGoogle Scholar
Li, L., Zhang, P., Liao, X. & Zhang, K. 2005 Multiplicity of nonlinear thermal convection in a spherical shell. Phys. Rev. E 71, 016301.CrossRefGoogle Scholar
Loukopoulos, V.C. 2004 Taylor vortices in annular heated spherical flow at medium and large aspect ratios. Phys. Fluids 17, 018108.CrossRefGoogle Scholar
Mamun, C.K. & Tuckerman, L.S. 1995 Asymmetry and Hopf bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.CrossRefGoogle Scholar
Mannix, P. 2020 Transitions and bistability of thermal convection between differentially rotating spherical shells. PhD thesis, Imperial College London.Google Scholar
Marcus, P.S. & Tuckerman, L.S. 1987 a Simulation of flow between concentric rotating spheres. Part 1. Steady states. J. Fluid Mech. 185, 1–30.CrossRefGoogle Scholar
Marcus, P.S. & Tuckerman, L.S. 1987 b Simulation of flow between concentric rotating spheres. Part 2. Transitions. J. Fluid Mech. 185, 31–65.CrossRefGoogle Scholar
Matthews, P.C. 2003 Pattern formation on a sphere. Phys. Rev. E 67, 036206.CrossRefGoogle Scholar
Mavromatis, H.A. & Alassar, R.S. 1999 A generalized formula for the integral of three associated Legendre polynomials. Appl. Maths Lett. 2, 101–105.CrossRefGoogle Scholar
McKinnon, W.B. 1999 Convective instability in europa's floating ice shell. Geophys. Res. Lett. 26 (7), 951–954.CrossRefGoogle Scholar
McKinnon, W.B. 2006 On convection in ice i shells of outer solar system bodies, with detailed application to callisto. Icarus 183 (2), 435–450.CrossRefGoogle Scholar
Mitri, G. & Showman, A.P. 2008 Thermal convection in ice-i shells of Titan and Enceladus. Icarus 193 (2), 387–396.CrossRefGoogle Scholar
Moore, D.R. & Weiss, N.O. 1973 Two-dimensional Rayleigh–Benard convection. J. Fluid Mech. 58 (2), 289–312.CrossRefGoogle Scholar
Munson, B.R. & Joseph, D.D. 1971 a Viscous incompressible flow between concentric rotating spheres. Part 1. Basic flow. J. Fluid Mech. 49 (2), 289–303.CrossRefGoogle Scholar
Munson, B.R. & Joseph, D.D. 1971 b Viscous incompressible flow between concentric rotating spheres. Part 2. Hydrodynamic stability. J. Fluid Mech. 49, 305–318.CrossRefGoogle Scholar
Nadiga, B.T. & Aurnou, J.M. 2008 A tabletop demonstration of atmospheric dynamics: baroclinic instability. Oceanography 21 (4), 196–201.CrossRefGoogle Scholar
Nimmo, F. & Pappalardo, R.T. 2016 Ocean worlds in the outer solar system. J. Geophys. Res. 121 (8), 1378–1399.CrossRefGoogle Scholar
Peale, S.J., Cassen, P. & Reynolds, R.T. 1979 Melting of Io by tidal dissipation. Science 203 (4383), 892–894.CrossRefGoogle ScholarPubMed
van der Poel, E., Stevens, R. & Lohse, D. 2011 Connecting flow structures and heat flux in turbulent Rayleigh-Bénard convection. Phys. Rev. E 84 (4), 045303.CrossRefGoogle ScholarPubMed
Proudman, J. & Lamb, H. 1916 On the motion of solids in a liquid possessing vorticity. Proc. R. Soc. Lond. A 92 (642), 408–424.Google Scholar
Ravelet, F., Marié, L., Chiffaudel, A. & Daviaud, F. 2004 Multistability and memory effect in a highly turbulent flow: experimental evidence for a global bifurcation. Phys. Rev. Lett. 93, 164501.CrossRefGoogle Scholar
Rayleigh, Lord 1916 On convection currents in a horizontal layer of fluid, when the higher temperature is on the under side. Phil. Mag. 32 (192), 529–546.CrossRefGoogle Scholar
Šil'nikov, L.P. 1970 A contribution to the problem of the structure of an extended neighborhood of a rough equilibrium state of saddle-foucs type. Maths USSR-Sbornik 10 (1), 91–102.CrossRefGoogle Scholar
Sreenivasan, K.R., Bershadskii, A. & Niemela, J.J. 2002 Mean wind and its reversal in thermal convection. Phys. Rev. E 65, 056306.CrossRefGoogle ScholarPubMed
Stewartson, K. 1953 On the flow between two rotating coaxial disks. Math. Proc. Camb. Phil. Soc. 49 (2), 333–341.CrossRefGoogle Scholar
Taylor, G.I. 1923 Stability of a viscous liquid contained between two rotating cylinders. Proc. R. Soc. Lond. A 102 (718), 541–542.Google Scholar
Travnikov, V., Zaussinger, F., Beltrame, P. & Egbers, C. 2017 Influence of the temperature- dependent viscosity on convective flow in the radial force field. Phys. Rev. E 96, 023108.CrossRefGoogle ScholarPubMed
Trefethen, L.N. 2000 Spectral Methods in Matlab. SIAM.CrossRefGoogle Scholar
Tyler, R.H. 2008 Strong ocean tidal flow and heating on moons of the outer planets. Nature 456, 770–772.CrossRefGoogle ScholarPubMed
Uecker, H., Wetzel, D. & Rademacher, J.D.M. 2014 pde2path - a matlab package for continuation and bifurcation in 2d elliptic systems. Numer. Math. 7 (1), 58–106.Google Scholar
van der Veen, R.C.A., Huisman, S.G., Dung, On-Yu, Tang, Ho L., Sun, C. & Lohse, D. 2016 Exploring the phase space of multiple states in highly turbulent Taylor–Couette flow. Phys. Rev. Fluids 1, 024401.CrossRefGoogle Scholar
Weiss, S. & Ahlers, G. 2013 Effect of tilting on turbulent convection: cylindrical samples with aspect ratio $\gamma = 0.50$. J. Fluid Mech. 715, 314–334.CrossRefGoogle Scholar
Wilson, A. & Kerswell, R.R. 2018 Can libration maintain Enceladus's ocean? Earth Planet. Sci. Lett. 500, 41–46.CrossRefGoogle Scholar
Wimmer, M. 1976 Experiments on a viscous fluid flow between concentric rotating spheres. J. Fluid Mech. 78 (2), 317–335.CrossRefGoogle Scholar
Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transitions in turbulent thermal convection. Phys. Fluids 20 (5), 055104.CrossRefGoogle Scholar
Yanase, S., Mizushima, J. & Araki, K. 1995 Multiple solutions for a flow between two concentric spheres with different temperatures and their stability. J. Phys. Soc. Japan 64 (7), 2433–2443.CrossRefGoogle Scholar
Zhang, K. & Liao, X. 2017 Theory and Modeling of Rotating Fluids, Convection, Intertial Waves and Precession. Cambridge.CrossRefGoogle Scholar
Zimmerman, D.S., Triana, S.A. & Lathrop, D.P. 2011 Bi-stability in turbulent, rotating spherical Couette flow. Phys. Fluids 23 (6), 065104.CrossRefGoogle Scholar

Mannix and Mestel supplementary movie 1

This movie shows the polar plume oscillation for Re_1 = 5 and Ra = 8'000 with d=3, Pr = 10. The plume which closely resembles a mushroom cloud of hot fluid travels radially outwards from the inner sphere. Upon reaching the outer sphere it is deflected in the polar direction and diffuses.

Download Mannix and Mestel supplementary movie 1(Video)
Video 2.9 MB

Mannix and Mestel supplementary movie 2

This movie show the equatorial jet for Re_1=40, Ra=30'000 with d=3,Pr=10. The jet which resembles a cantilever beam, extends outwards at the equator and oscillates back and forth in the polar direction. The presence of a strong thermal boundary layer is indicated by the closely bunched contours near the inner sphere.

Download Mannix and Mestel supplementary movie 2(Video)
Video 3.1 MB

Mannix and Mestel supplementary movie 3

This movie show the trajectories of the equatorial jet's limit cycle for Re_1=40, Ra=30'000 with d=3,Pr=10. The fast winding loops are followed by slow passages as the cycle passes near saddle-node points.

Download Mannix and Mestel supplementary movie 3(Video)
Video 531.4 KB

Mannix and Mestel supplementary movie 4

This movie shows the polar plumes for Re_1=40, Ra=35'000 with d=3,Pr=10. The narrow thermal plumes which emerges from a strong radial boundary layer is directed upwards towards the pole near the inner sphere. Near the annulus centre-line the plume waves back and forth due to the influence of Ekman pumping which pushes it away form the axis and the large convection cell which forces it back towards the axis.

Download Mannix and Mestel supplementary movie 4(Video)
Video 6 MB

Mannix and Mestel supplementary movie 5

This movie shows the polar plumes for Re_1=40, Ra=35'000 with d=3,Pr=10. The fast winding loops are followed by slow passages as the cycle passes near a saddle-node point.

Download Mannix and Mestel supplementary movie 5(Video)
Video 588.2 KB