Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-24T18:49:13.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Bidensity particle-laden exchange flows in a vertical duct

Published online by Cambridge University Press:  23 March 2020

N. Mirzaeian ,
F. Y. Testik  and
K. Alba Open the ORCID record for K. Alba [Opens in a new window]
N. Mirzaeian
Affiliation:
Department of Applied Physical Sciences, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599, USA
F. Y. Testik
Affiliation:
Department of Civil and Environmental Engineering, University of Texas at San Antonio, San Antonio, TX 78249, USA
K. Alba*
Affiliation:
Department of Engineering Technology, University of Houston, Houston, TX 77204, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

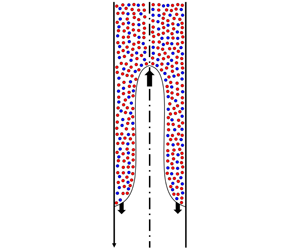
Buoyancy-driven exchange flow in a vertical duct is studied theoretically for a light pure fluid and a heavy fluid. The latter is a suspension composed of a Newtonian fluid and two populations of negatively buoyant particles of the same size but different densities (bidensity). In a previous study (Mirzaeian & Alba, J. Fluid Mech., vol. 847, 2018, pp. 134–160), the authors developed a lubrication model for monodensity suspension of particles of uniform size. The main observation of the monodensity study was the discovery of particle-enriched zones near heavy and light fluid fronts due to the relative motion of particles and the fluid. Distinct from the previous work, here, mismatched densities instigate a relative motion of lighter and heavier particles in addition to the movement of fluids. Other than the previously observed enrichment case, the bidensity case gives rise to a novel flow regime where there is enrichment of heavy particles but depletion of light particles near the interface. The transition to this regime is governed by a balance between the densities of heavy and light particles as well as those of light and carrying fluids for a given choice of initial volume fractions of particles. Such density balance is characterized by two dimensionless parameters comprising light and heavy particle-to-carrying-fluid density ratios. The transition mechanism is studied through additional simulations, revealing that the former increases with initial volume fraction of particles of either type, while the latter contrarily decreases. The effect of other parameters on the flow are discussed within the context of the paper.

JFM classification

Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 891 , 25 May 2020 , A18
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acrivos, A., Fan, X. & Mauri, R. 1994 On the measurement of the relative viscosity of suspensions. J. Rheol. 38 (5), 1285–1296.CrossRefGoogle Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2013a Miscible density-unstable displacement flows in inclined tube. Phys. Fluids 25, 067101.CrossRefGoogle Scholar
Alba, K., Taghavi, S. M. & Frigaard, I. A. 2013b A weighted residual method for two-layer non-Newtonian channel flows: steady-state results and their stability. J. Fluid Mech. 731, 509–544.CrossRefGoogle Scholar
Botchwey, E. A., Pollack, S. R., Levine, E. M., Johnston, E. D. & Laurencin, C. T. 2004 Quantitative analysis of three-dimensional fluid flow in rotating bioreactors for tissue engineering. J. Biomed. Mater. Res. A 69 (2), 205–215.CrossRefGoogle ScholarPubMed
Choux, C., Druitt, T. & Thomas, N. 2004 Stratification and particle segregation in flowing polydisperse suspensions, with applications to the transport and sedimentation of pyroclastic density currents. J. Volcanol. Geotherm. Res. 138 (3–4), 223–241.CrossRefGoogle Scholar
Cook, B. P.2007 Lubrication models for particle-laden thin films. PhD thesis, University of California, Los Angeles.Google Scholar
Cook, B. P., Alexandrov, O. & Bertozzi, A. L. 2009 Linear stability of particle-laden thin films. Eur. Phys. J. Spec. Top. 166 (1), 77–81.CrossRefGoogle Scholar
Cook, B. P., Bertozzi, A. L. & Hosoi, A. E. 2008 Shock solutions for particle-laden thin films. SIAM J. Appl. Maths 68 (3), 760–783.CrossRefGoogle Scholar
Cowan, K. M. & Hale, A. H.1994 Cement plug for well abandonment. US Patent 5,343,952.Google Scholar
Davis, R. H. & Acrivos, A. 1985 Sedimentation of noncolloidal particles at low Reynolds numbers. Annu. Rev. Fluid Mech. 17 (1), 91–118.CrossRefGoogle Scholar
Hasnain, A. & Alba, K. 2017 Buoyant displacement flow of immiscible fluids in inclined ducts: a theoretical approach. Phys. Fluids 29, 052102.CrossRefGoogle Scholar
Hasnain, A., Segura, E. & Alba, K. 2017 Buoyant displacement flow of immiscible fluids in inclined pipes. J. Fluid Mech. 824, 661–687.CrossRefGoogle Scholar
Konidena, S., Reddy, K. A. & Singh, A. 2019 Dynamics of bidensity particle suspensions in a horizontal rotating cylinder. Phys. Rev. E 99 (1), 013111.Google Scholar
Krishnan, G. & Leighton, D. T. 1995 Dynamic viscous resuspension of bidisperse suspensionsi. Effective diffusivity. Intl J. Multiphase Flow 21 (5), 721–732.CrossRefGoogle Scholar
Kurganov, A. & Tadmor, E. 2000 New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations. J. Comput. Phys. 160 (1), 241–282.CrossRefGoogle Scholar
Lee, S., Mavromoustaki, A., Urdaneta, G., Huang, K. & Bertozzi, A. L. 2014 Experimental investigation of bidensity slurries on an incline. Granul. Matt. 16 (2), 269–274.CrossRefGoogle Scholar
Lee, S., Wong, J. & Bertozzi, A. L. 2015 Equilibrium theory of bidensity particle-laden flows on an incline. In Mathematical Modelling and Numerical Simulation of Oil Pollution Problems, pp. 85–97. Springer.Google Scholar
Leighton, D. & Acrivos, A. 1986 Viscous resuspension. Chem. Engng Sci. 41 (6), 1377–1384.CrossRefGoogle Scholar
Leighton, D. & Acrivos, A. 1987 The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 181, 415–439.CrossRefGoogle Scholar
Matson, G. P. & Hogg, A. J. 2012 Viscous exchange flows. Phys. Fluids 24 (2), 023102.CrossRefGoogle Scholar
Mirzaeian, N. & Alba, K. 2018a Monodisperse particle-laden exchange flows in a vertical duct. J. Fluid Mech. 847, 134–160.CrossRefGoogle Scholar
Mirzaeian, N. & Alba, K. 2018b Particle-laden exchange flows in inclined pipes. Phys. Rev. Fluids 3, 114301.CrossRefGoogle Scholar
Murisic, N., Pausader, B., Peschka, D. & Bertozzi, A. L. 2013 Dynamics of particle settling and resuspension in viscous liquid films. J. Fluid Mech. 717, 203–231.CrossRefGoogle Scholar
Pednekar, S., Chun, J. & Morris, J. F. 2018 Bidisperse and polydisperse suspension rheology at large solid fraction. J. Rheol. 62 (2), 513–526.CrossRefGoogle Scholar
Phillips, R. J., Armstrong, R. C., Brown, R. A., Graham, A. L. & Abbott, J. R. 1992 A constitutive equation for concentrated suspensions that accounts for shear-induced particle migration. Phys. Fluids A 4 (1), 30–40.CrossRefGoogle Scholar
Press, W. H. 1992 Numerical Recipes in Fortran 77: The Art of Scientific Computing. Cambridge University Press.Google Scholar
Revay, J. M. & Higdon, J. J. L. 1992 Numerical simulation of polydisperse sedimentation: equal-sized spheres. J. Fluid Mech. 243, 15–32.CrossRefGoogle Scholar
Schaflinger, U., Acrivos, A. & Zhang, K. 1990 Viscous resuspension of a sediment within a laminar and stratified flow. Intl J. Multiphase Flow 16 (4), 567–578.CrossRefGoogle Scholar
Segre, G. & Silberberg, A. 1961 Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210.CrossRefGoogle Scholar
Seon, T., Hulin, J.-P., Salin, D., Perrin, B. & Hinch, E. J. 2004 Buoyant mixing of miscible fluids in tilted tubes. Phys. Fluids 16, L103–L106.CrossRefGoogle Scholar
Sierou, A. & Brady, J. F. 2004 Shear-induced self-diffusion in non-colloidal suspensions. J. Fluid Mech. 506, 285–314.CrossRefGoogle Scholar
Spaid, M. A. & Homsy, G. M. 1996 Stability of Newtonian and viscoelastic dynamic contact lines. Phys. Fluids 8 (2), 460–478.CrossRefGoogle Scholar
Taghavi, S. M., Alba, K., Seon, T., Wielage-Burchard, K., Martinez, D. M. & Frigaard, I. A. 2012 Miscible displacement flows in near-horizontal ducts at low Atwood number. J. Fluid Mech. 696, 175–214.CrossRefGoogle Scholar
Taghavi, S. M., Seon, T., Martinez, D. M. & Frigaard, I. A. 2009 Buoyancy-dominated displacement flows in near-horizontal channels: the viscous limit. J. Fluid Mech. 639, 1–35.CrossRefGoogle Scholar
Tripathi, A. & Acrivos, A. 1999 Viscous resuspension in a bidensity suspension. Intl J. Multiphase Flow 25 (1), 1–14.CrossRefGoogle Scholar
Weiland, R. H., Fessas, Y. P. & Ramarao, B. V. 1984 On instabilities arising during sedimentation of two-component mixtures of solids. J. Fluid Mech. 142, 383–389.CrossRefGoogle Scholar
Wong, J. T.2017 Modeling and analysis of thin-film incline flow: bidensity suspensions and surface tension effects. PhD thesis, University of California, Los Angeles, Los Angeles, United States.Google Scholar
Wong, J. T. & Bertozzi, A. L. 2016 A conservation law model for bidensity suspensions on an incline. Physica D 330, 47–57.Google Scholar
Zhou, J., Dupuy, B., Bertozzi, A. L. & Hosoi, A. E. 2005 Theory for shock dynamics in particle-laden thin films. Phys. Rev. Lett. 94 (11), 117803.CrossRefGoogle ScholarPubMed