Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-19T03:46:20.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Beta-plane turbulence above monoscale topography

Published online by Cambridge University Press:  24 August 2017

Navid C. Constantinou Open the ORCID record for Navid C. Constantinou [Opens in a new window]  and
William R. Young Open the ORCID record for William R. Young [Opens in a new window]
Navid C. Constantinou*
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093-0213, USA
William R. Young
Affiliation:
Scripps Institution of Oceanography, University of California San Diego, La Jolla, CA 92093-0213, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Using a one-layer quasi-geostrophic model, we study the effect of random monoscale topography on forced beta-plane turbulence. The forcing is a uniform steady wind stress that produces both a uniform large-scale zonal flow 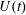$U(t)$ and smaller-scale macroturbulence characterized by standing and transient eddies. The large-scale flow 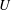$U$ is retarded by a combination of Ekman drag and the domain-averaged topographic form stress produced by the eddies. The topographic form stress typically balances most of the applied wind stress, while the Ekman drag provides all of the energy dissipation required to balance the wind work. A collection of statistically equilibrated numerical solutions delineate the main flow regimes and the dependence of the time average of 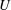$U$ on parameters such as the planetary potential vorticity (PV) gradient 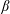$\unicode[STIX]{x1D6FD}$ and the statistical properties of the topography. We obtain asymptotic scaling laws for the strength of the large-scale flow 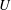$U$ in the limiting cases of weak and strong forcing. If 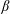$\unicode[STIX]{x1D6FD}$ is significantly smaller than the topographic PV gradient, the flow consists of stagnant pools attached to pockets of closed geostrophic contours. The stagnant dead zones are bordered by jets and the flow through the domain is concentrated into a narrow channel of open geostrophic contours. In most of the domain, the flow is weak and thus the large-scale flow 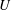$U$ is an unoccupied mean. If 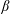$\unicode[STIX]{x1D6FD}$ is comparable to, or larger than, the topographic PV gradient, then all geostrophic contours are open and the flow is uniformly distributed throughout the domain. In this open-contour case, there is an ‘eddy saturation’ regime in which 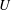$U$ is insensitive to large changes in the wind stress. We show that eddy saturation requires strong transient eddies that act effectively as PV diffusion. This PV diffusion does not alter the kinetic energy of the standing eddies, but it does increase the topographic form stress by enhancing the correlation between the topographic slope and the standing-eddy pressure field. Using bounds based on the energy and enstrophy power integrals, we show that as the strength of the wind stress increases, the flow transitions from a regime in which the form stress balances most of the wind stress to a regime in which the form stress is very small and large transport ensues.

JFM classification

Geophysical and Geological Flows: Geostrophic turbulence Geophysical and Geological Flows: Quasi-geostrophic flows Geophysical and Geological Flows: Topographic effects
Type
Papers
Information
Journal of Fluid Mechanics , Volume 827 , 25 September 2017 , pp. 415 - 447
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abernathey, R. & Cessi, P. 2014 Topographic enhancement of eddy efficiency in baroclinic equilibration. J. Phys. Oceanogr. 44 (8), 2107–2126.Google Scholar
Arbic, B. K. & Flierl, G. R. 2004 Baroclinically unstable geostrophic turbulence in the limits of strong and weak bottom Ekman friction: application to midocean eddies. J. Phys. Oceanogr. 34 (10), 2257–2273.2.0.CO;2>CrossRefGoogle Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1, 177–190.CrossRefGoogle Scholar
Böning, C. W., Dispert, A., Visbeck, M., Rintoul, S. R. & Schwarzkopf, F. U. 2008 The response of the Antarctic Circumpolar Current to recent climate change. Nat. Geosci. 1 (1), 864–869.Google Scholar
Bretherton, F. P. & Karweit, M. 1975 Mid-ocean mesoscale modeling. In Numerical Models of Ocean Circulation, pp. 237–249. National Academy of Sciences.Google Scholar
Carnevale, G. F. & Frederiksen, J. S. 1987 Nonlinear stability and statistical mechanics of flow over topography. J. Fluid Mech. 175, 157–181.CrossRefGoogle Scholar
Charney, J. G. & Devore, J. G. 1979 Multiple flow equilibria in the atmosphere and blocking. J. Atmos. Sci. 36, 1205–1216.2.0.CO;2>CrossRefGoogle Scholar
Charney, J. G., Shukla, J. & Mo, K. C. 1981 Comparison of a barotropic blocking theory with observation. J. Atmos. Sci. 38 (4), 762–779.Google Scholar
Constantinou, N. C. 2017 A barotropic model of eddy saturation. J. Phys. Oceanogr. (submitted) arXiv:1703.06594.Google Scholar
Cox, S. M. & Matthews, P. C. 2002 Exponential time differencing for stiff systems. J. Comput. Phys. 176 (2), 430–455.Google Scholar
Davey, M. K. 1980 A quasi-linear theory for rotating flow over topography. Part 1. Steady 𝛽-plane channel. J. Fluid Mech. 99 (02), 267–292.CrossRefGoogle Scholar
Donohue, K. A., Tracey, K. L., Watts, D. R., Chidichimo, M. P. & Chereskin, T. K. 2016 Mean Antarctic Circumpolar Current transport measured in Drake Passage. Geophys. Res. Lett. 43, 11760–11767.Google Scholar
Farneti, R., Downes, S. M., Griffies, S. M., Marsland, S. J., Behrens, E., Bentsen, M., Bi, D., Bias-toch, A., Böning, C., Bozec, A. et al. 2015 An assessment of Antarctic Circumpolar Current and Southern Ocean meridional overturning circulation during 1958–2007 in a suite of interannual CORE-II simulations. Ocean Model. 93, 84–120.Google Scholar
Farneti, R., Delworth, T. L., Rosati, A. J., Griffies, S. M. & Zeng, F. 2010 The role of mesoscale eddies in the rectification of the Southern Ocean response to climate change. J. Phys. Oceanogr. 40, 1539–1557.Google Scholar
Firing, Y. L., Chereskin, T. K. & Mazloff, M. R. 2011 Vertical structure and transport of the Antarctic Circumpolar Current in Drake Passage from direct velocity observations. J. Geophys. Res. 116 (C8), C08015.Google Scholar
Goff, J. A. 2010 Global prediction of abyssal hill root-mean-square heights from small-scale altimetric gravity variability. J. Geophys. Res. 115 (B12), B12104.Google Scholar
Gruzinov, A. V., Isichenko, M. B. & Kalda, Ya. L. 1990 Two-dimensional turbulent diffusion. Zh. Eksp. Teor. Fiz. 97, 476 [Sov. Phys. JETP 70, 263 (1990)].Google Scholar
Hallberg, R. & Gnanadesikan, A. 2001 An exploration of the role of transient eddies in determining the transport of a zonally reentrant current. J. Phys. Oceanogr. 31 (11), 3312–3330.Google Scholar
Hallberg, R. & Gnanadesikan, A. 2006 The role of eddies in determining the structure and response of the wind-driven Southern Hemisphere overturning: results from the modeling eddies in the Southern Ocean (MESO) project. J. Phys. Oceanogr. 36, 2232–2252.CrossRefGoogle Scholar
Hart, J. E. 1979 Barotropic quasi-geostrophic flow over anisotropic mountains. J. Atmos. Sci. 36 (9), 1736–1746.2.0.CO;2>CrossRefGoogle Scholar
Hogg, A. McC. & Blundell, J. R. 2006 Interdecadal variability of the Southern Ocean. J. Phys. Oceanogr. 36, 1626–1645.Google Scholar
Hogg, A. McC., Meredith, M. P., Blundell, J. R. & Wilson, C. 2008 Eddy heat flux in the Southern Ocean: response to variable wind forcing. J. Clim. 21, 608–620.Google Scholar
Hogg, A. McC., Meredith, M. P., Chambers, D. P., Abrahamsen, E. P., Hughes, C. W. & Morrison, A. K. 2015 Recent trends in the Southern Ocean eddy field. J. Geophys. Res. 120, 1–11.Google Scholar
Holloway, G. 1987 Systematic forcing of large-scale geophysical flows by eddy–topography interaction. J. Fluid Mech. 184, 463–476.CrossRefGoogle Scholar
Ingersoll, A. P. 1969 Inertial Taylor columns and Jupiter’s Great Red Spot. J. Atmos. Sci. 26, 744–752.Google Scholar
Isichenko, M. B. 1992 Percolation, statistical topography, and transport in random media. Rev. Mod. Phys. 64 (4), 961–1043.Google Scholar
Isichenko, M. B., Kalda, Ya. L., Tatarinova, E. B., Tel’kovskaya, O. V. & Yan’kov, V. V. 1989 Diffusion in a medium with vortex flow. Zh. Eksp. Teor. Fiz. 96, 913–925; [Sov. Phys. JETP 69, 3 (1989)].Google Scholar
Källén, E. 1982 Bifurcation properties of quasi-geostrophic, barotropic models and their relation to atmospheric blocking. Tellus 34 (3), 255–265.CrossRefGoogle Scholar
Kassam, A.-K. & Trefethen, L. N. 2005 Fourth-order time-stepping for stiff PDEs. SIAM J. Sci. Comput. 26 (4), 1214–1233.CrossRefGoogle Scholar
Koenig, Z., Provost, C., Park, Y.-H., Ferrari, R. & Sennéchael, N. 2016 Anatomy of the Antarctic Circumpolar Current volume transports through Drake Passage. J. Geophys. Res. 121 (4), 2572–2595.CrossRefGoogle Scholar
Legras, B. & Ghil, M. 1985 Persistent anomalies, blocking and variations in atmospheric predictability. J. Atmos. Sci. 42, 433–471.Google Scholar
Mak, J., Marshall, D. P., Maddison, J. R. & Bachman, S. D. 2017 Emergent eddy saturation from an energy constrained parameterisation. Ocean Model. 112, 125–138.Google Scholar
Marshall, G. J. 2003 Trends in the Southern Annular Mode from observations and reanalyses. J. Clim. 16, 4134–4143.Google Scholar
Marshall, D. P., Abhaum, M. H. P., Maddison, J. R., Munday, D. R. & Novak, L. 2016 Eddy saturation and frictional control of the Antarctic Circumpolar Current. Geophys. Res. Lett. 44, 1–7.Google Scholar
Meredith, M. P., Naveira Garabato, A. C., Hogg, A. McC. & Farneti, R. 2012 Sensitivity of the overturning circulation in the Southern Ocean to decadal changes in wind forcing. J. Clim. 25, 99–110.Google Scholar
Morisson, A. K. & Hogg, A. McC. 2013 On the relationship between Southern Ocean overturning and ACC transport. J. Phys. Oceanogr. 43, 140–148.Google Scholar
Munday, D. R., Johnson, H. L. & Marshall, D. P. 2013 Eddy saturation of equilibrated circumpolar currents. J. Phys. Oceanogr. 43, 507–532.Google Scholar
Munk, W. H. & Palmén, E. 1951 Note on the dynamics of the Antarctic Circumpolar Current. Tellus 3, 53–55.CrossRefGoogle Scholar
Nadeau, L.-P. & Ferrari, R. 2015 The role of closed gyres in setting the zonal transport of the Antarctic Circumpolar Current. J. Phys. Oceanogr. 45, 1491–1509.Google Scholar
Nadeau, L.-P. & Straub, D. N. 2009 Basin and channel contributions to a model Antarctic Circumpolar Current. J. Phys. Oceanogr. 39 (4), 986–1002.CrossRefGoogle Scholar
Nadeau, L.-P. & Straub, D. N. 2012 Influence of wind stress, wind stress curl, and bottom friction on the transport of a model Antarctic Circumpolar Current. J. Phys. Oceanogr. 42 (1), 207–222.Google Scholar
Pedlosky, J. 1981 Resonant topographic waves in barotropic and baroclinic flows. J. Atmos. Sci. 38 (12), 2626–2641.Google Scholar
Rambaldi, S. & Flierl, G. R. 1983 Form drag instability and multiple equilibria in the barotropic case Il. Nuovo Cimento C 6 (5), 505–522.Google Scholar
Rambaldi, S. & Mo, K. C. 1984 Forced stationary solutions in a barotropic channel: multiple equilibria and theory of nonlinear resonance. J. Atmos. Sci. 41 (21), 3135–3146.Google Scholar
Rhines, P. B. & Young, W. R. 1982 Homogenization of potential vorticity in planetary gyres. J. Fluid Mech. 122, 347–367.Google Scholar
Rhines, P. B. & Young, W. R. 1983 How rapidly is a passive scalar mixed within closed streamlines? J. Fluid Mech. 133, 133–145.Google Scholar
Straub, D. N. 1993 On the transport and angular momentum balance of channel models of the Antarctic Circumpolar Current. J. Phys. Oceanogr. 23, 776–782.Google Scholar
Swart, N. C. & Fyfe, J. C. 2012 Observed and simulated changes in the Southern Hemisphere surface westerly wind-stress. Geophys. Res. Lett. 39 (16), L16711.Google Scholar
Tansley, C. E. & Marshall, D. P. 2001 On the dynamics of wind-driven circumpolar currents. J. Phys. Oceanogr. 31, 3258–3273.Google Scholar
Thompson, D. W. J. & Solomon, S. 2002 Interpretation of recent Southern Hemisphere climate change. Science 296, 895–899.Google Scholar
Tung, K.-K. & Rosenthal, A. J. 1985 Theories of multiple equilibria – a critical reexamination. Part I: barotropic models. J. Atmos. Sci. 42, 2804–2819.2.0.CO;2>CrossRefGoogle Scholar
Uchimoto, K. & Kubokawa, A. 2005 Form drag caused by topographically forced waves in a barotropic 𝛽 channel: effect of higher mode resonance. J. Oceanogr. 61 (2), 197–211.Google Scholar
Yoden, S. 1985 Bifurcation properties of a quasi-geostrophic, barotropic, low-order model with topography. J. Meteor. Soc. Japan. Ser. II 63 (4), 535–546.Google Scholar

Constantinou et al. supplementary movie 1

The evolution from rest of $q=\zeta + \eta$ and of the total streamfunction $\psi-U y$ for the example case with closed-geostrophic contours that is presented in section 3.4.

Download Constantinou et al. supplementary movie 1(Video)
Video 68.1 MB

Constantinou et al. supplementary movie 2

The evolution from rest of $q=\zeta + \eta$ and of the total streamfunction $\psi-U y$ for the example case with closed-geostrophic contours that is presented in section 3.5.

Download Constantinou et al. supplementary movie 2(Video)
Video 77.7 MB