Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T17:39:56.501Z Has data issue: false hasContentIssue false
  • English
  • Français

Backflow from a model fracture network: an asymptotic investigation

Published online by Cambridge University Press:  14 February 2019

Asaf Dana Open the ORCID record for Asaf Dana [Opens in a new window] ,
Gunnar G. Peng Open the ORCID record for Gunnar G. Peng [Opens in a new window] ,
Howard A. Stone ,
Herbert E. Huppert  and
Guy Z. Ramon Open the ORCID record for Guy Z. Ramon [Opens in a new window]
Asaf Dana
Affiliation:
The Nancy and Stephen Grand Technion Energy Program, and Department of Civil and Environmental Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
Gunnar G. Peng
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Howard A. Stone
Affiliation:
Department of Mechanical and Aerospace Engineering, Princeton University, Princeton, NJ 08544, USA
Herbert E. Huppert
Affiliation:
Institute of Theoretical Geophysics, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
Guy Z. Ramon*
Affiliation:
The Nancy and Stephen Grand Technion Energy Program, and Department of Civil and Environmental Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a model for predicting the flow resulting from the relaxation of pre-strained, fluid-filled, elastic network structures. This model may be useful for understanding relaxation processes in various systems, e.g. deformable microfluidic systems or by-products from hydraulic fracturing operations. The analysis is aimed at elucidating features that may provide insight on the rate of fluid drainage from fracturing operations. The model structure is a bifurcating network made of fractures with uniform length and elastic modulus, which allows for general self-similar branching and variation in fracture length and rigidity between fractures along the flow path. A late-time 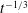$t^{-1/3}$ power law is attained and the physical behaviour can be classified into four distinct regimes that describe the late-time dynamics based on the location of the bulk of the fluid volume (which shifts away from the outlet as branching is increased) and pressure drop (which shifts away from the outlet as rigidity is increased upstream) along the network. We develop asymptotic solutions for each of the regimes, predicting the late-time flux and evolution of the pressure distribution. The effects of the various parameters on the outlet flux and the network’s drainage efficiency are investigated and show that added branching and a decrease in rigidity upstream tend to increase drainage time.

JFM classification

Low-Reynolds-number flows: Lubrication theory Low-Reynolds-number flows: Porous media
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 864 , 10 April 2019 , pp. 899 - 924
Check for updates
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

These two authors contributed equally.

References

Bonnet, E., Bour, O., Odling, N. E., Davy, P., Main, I., Cowie, P. & Berkowitz, B. 2001 Scaling of fracture systems in geological media. Rev. Geophys. 39 (3), 347–383.Google Scholar
Chau, V. T., Bažant, Z. P. & Su, Y. 2016 Growth model for large branched three-dimensional hydraulic crack system in gas or oil shale. Phil. Trans. R. Soc. Lond. A 374 (2078), 20150418.Google Scholar
Dana, A., Zheng, Z., Peng, G. G., Stone, H. A., Huppert, H. E. & Ramon, G. Z. 2018 Dynamics of viscous backflow from a model fracture network. J. Fluid Mech. 836, 828–849.Google Scholar
Holditch, S. A. 2007 Hydraulic fracturing: overview, trends, issues. Drilling Contractor 63, 116–118.Google Scholar
Jinzhou, Z., Lan, R., Cheng, S. & Li, Y. 2018 Latest research progresses in network fracturing theories and technologies for shale gas reservoirs. Natural Gas Industry B 5 (5), 533–546.Google Scholar
King, G. E. 2010 Thirty years of gas shale fracturing: what have we learned? In SPE Annual Technical Conference and Exhibition. Society of Petroleum Engineers.Google Scholar
Lai, C. Y., Zheng, Z., Dressaire, E., Ramon, G. Z., Huppert, H. E. & Stone, H. A. 2016 Elastic relaxation of fluid-driven cracks and the resulting backflow. Phys. Rev. Lett. 117 (26), 268001.Google Scholar
Marck, J. & Detournay, E. 2013 Withdrawal of fluid from a poroelastic layer. In Poromechanics V: Proceedings of the Fifth Biot Conference on Poromechanics, pp. 1271–1278. ASCE.Google Scholar
Marck, J., Savitski, A. A. & Detournay, E. 2015 Line source in a poroelastic layer bounded by an elastic space. Intl J. Numer. Anal. Meth. Geomech. 39 (14), 1484–1505.Google Scholar
Matia, Y. & Gat, A. D. 2015 Dynamics of elastic beams with embedded fluid-filled parallel-channel networks. Soft Robotics 2 (1), 42–47.Google Scholar
Patzek, T. W., Male, F. & Marder, M. L. 2013 Gas production in the Barnett Shale obeys a simple scaling theory. Proc. Natl Acad. Sci. USA 110 (49), 19731–19736.Google Scholar
Santillán, D., Mosquera, J. C. & Cueto-Felgueroso, L. 2017 Fluid-driven fracture propagation in heterogeneous media: probability distributions of fracture trajectories. Phys. Rev. E 96 (5), 053002.Google Scholar
Weibel, D. B., Siegel, A. C., Lee, A., George, A. H. & Whitesides, G. M. 2007 Pumping fluids in microfluidic systems using the elastic deformation of poly(dimethylsiloxane). Lab on a Chip 7 (12), 1832–1836.Google Scholar