Article contents
Azimuthal velocity profiles in Rayleigh-stable Taylor–Couette flow and implied axial angular momentum transport
Published online by Cambridge University Press: 09 June 2015
Abstract
We present azimuthal velocity profiles measured in a Taylor–Couette apparatus, which has been used as a model of stellar and planetary accretion disks. The apparatus has a cylinder radius ratio of 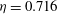 ${\it\eta}=0.716$, an aspect ratio of
${\it\eta}=0.716$, an aspect ratio of 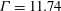 ${\it\Gamma}=11.74$, and the plates closing the cylinders in the axial direction are attached to the outer cylinder. We investigate angular momentum transport and Ekman pumping in the Rayleigh-stable regime. This regime is linearly stable and is characterized by radially increasing specific angular momentum. We present several Rayleigh-stable profiles for shear Reynolds numbers
${\it\Gamma}=11.74$, and the plates closing the cylinders in the axial direction are attached to the outer cylinder. We investigate angular momentum transport and Ekman pumping in the Rayleigh-stable regime. This regime is linearly stable and is characterized by radially increasing specific angular momentum. We present several Rayleigh-stable profiles for shear Reynolds numbers 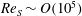 $\mathit{Re}_{S}\sim O(10^{5})$, for both
$\mathit{Re}_{S}\sim O(10^{5})$, for both 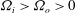 ${\it\Omega}_{i}>{\it\Omega}_{o}>0$ (quasi-Keplerian regime) and
${\it\Omega}_{i}>{\it\Omega}_{o}>0$ (quasi-Keplerian regime) and 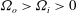 ${\it\Omega}_{o}>{\it\Omega}_{i}>0$ (sub-rotating regime), where
${\it\Omega}_{o}>{\it\Omega}_{i}>0$ (sub-rotating regime), where 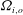 ${\it\Omega}_{i,o}$ is the inner/outer cylinder rotation rate. None of the velocity profiles match the non-vortical laminar Taylor–Couette profile. The deviation from that profile increases as solid-body rotation is approached at fixed
${\it\Omega}_{i,o}$ is the inner/outer cylinder rotation rate. None of the velocity profiles match the non-vortical laminar Taylor–Couette profile. The deviation from that profile increases as solid-body rotation is approached at fixed 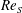 $\mathit{Re}_{S}$. Flow super-rotation, an angular velocity greater than those of both cylinders, is observed in the sub-rotating regime. The velocity profiles give lower bounds for the torques required to rotate the inner cylinder that are larger than the torques for the case of laminar Taylor–Couette flow. The quasi-Keplerian profiles are composed of a well-mixed inner region, having approximately constant angular momentum, connected to an outer region in solid-body rotation with the outer cylinder and attached axial boundaries. These regions suggest that the angular momentum is transported axially to the axial boundaries. Therefore, Taylor–Couette flow with closing plates attached to the outer cylinder is an imperfect model for accretion disk flows, especially with regard to their stability.
$\mathit{Re}_{S}$. Flow super-rotation, an angular velocity greater than those of both cylinders, is observed in the sub-rotating regime. The velocity profiles give lower bounds for the torques required to rotate the inner cylinder that are larger than the torques for the case of laminar Taylor–Couette flow. The quasi-Keplerian profiles are composed of a well-mixed inner region, having approximately constant angular momentum, connected to an outer region in solid-body rotation with the outer cylinder and attached axial boundaries. These regions suggest that the angular momentum is transported axially to the axial boundaries. Therefore, Taylor–Couette flow with closing plates attached to the outer cylinder is an imperfect model for accretion disk flows, especially with regard to their stability.
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 13
- Cited by



