Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-21T02:00:38.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Axial flow in a two-dimensional microchannel induced by a travelling temperature wave imposed at the bottom wall

Published online by Cambridge University Press:  13 June 2018

Chenguang Zhang ,
Harris Wong Open the ORCID record for Harris Wong [Opens in a new window]  and
Krishnaswamy Nandakumar
Chenguang Zhang
Affiliation:
Cain Department of Chemical Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
Harris Wong*
Affiliation:
Department of Mechanical and Industrial Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
Krishnaswamy Nandakumar
Affiliation:
Cain Department of Chemical Engineering, Louisiana State University, Baton Rouge, LA 70803, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Fluid flow in microchannels has wide industrial and scientific applications. Hence, it is important to explore different driving mechanisms. In this paper, we study the net transport or fluid pumping in a two-dimensional channel induced by a travelling temperature wave applied at the bottom wall. The Navier–Stokes equations with the Boussinesq approximation and the convection–diffusion heat equation are made dimensionless by the height of the channel and a velocity scale obtained by a dominant balance between buoyancy and viscous resistance in the momentum equation. The system of equations is transformed to an axial coordinate that moves with the travelling temperature wave, and we seek steady solutions in this moving frame. Four dimensionless numbers emerge from the governing equations and boundary conditions: the Reynolds number 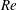$Re$, a Reynolds number 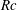$Rc$ based on the wave speed, the Prandtl number 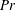$Pr$ and the dimensionless wavenumber 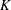$K$. The system of equations is solved by a finite-volume method and by a perturbation method in the limit 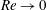$Re\rightarrow 0$. Surprisingly, the leading and first-order perturbation solutions agree well with the computed axial flow for 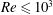$Re\leqslant 10^{3}$. 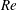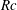Thus, the analytic perturbation solutions are used to study systematically the effects of $Re$, $Rc$, 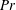$Pr$ and 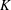$K$ on the dimensionless induced axial flow 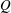$Q$. We find that 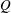$Q$ varies linearly with $Re$, and 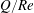$Q/Re$ versus any of the three remaining dimensionless groups always exhibits a maximum. The global maximum of 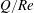$Q/Re$ in the parameter space is subsequently determined for the first time. This induced axial flow is driven solely by the Reynolds stress.

JFM classification

Waves/Free-surface Flows: Channel flow Convection: Convection Micro-/Nano-fluid dynamics: Microfluidics
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 848 , 10 August 2018 , pp. 1040 - 1072
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anna, S. L. 2016 Droplets and bubbles in microfluidic devices. Annu. Rev. Fluid Mech. 48, 285–309.Google Scholar
Baroud, C. N., Gallaire, F. & Dangla, R. 2010 Dynamics of microfluidic droplets. Lab on a Chip 10 (16), 2032–2045.Google Scholar
Davey, A. 1967 The motion of a fluid due to a moving source of heat at the boundary. J. Fluid Mech. 29 (1), 137–150.Google Scholar
Douglas, H. A., Mason, P. J. & Hinch, E. J. 1972 Motion due to a moving internal heat source. J. Fluid Mech. 54 (3), 469–480.Google Scholar
Eldabe, N. T. M., El-Sayed, M. F., Ghaly, a. Y. & Sayed, H. M. 2007 Mixed convective heat and mass transfer in a non-Newtonian fluid at a peristaltic surface with temperature-dependent viscosity. Arch. Appl. Mech. 78 (8), 599–624.Google Scholar
Fultz, D.1956 Studies in experimental hydrodynamics (1). Final Report, Hydrodynamics Lab. University of Chicago.Google Scholar
Halley, E. 1686 An historical account of the trade winds, and monsoons, observable in the seas between and near the tropicks, with an attempt to assign the phisical cause of the said winds, by E. Halley. Philos. Trans. R. Soc. Lond. 16 (179–191), 153–168.Google Scholar
Hinch, E. J. & Schubert, G. 1971 Strong streaming induced by a moving thermal wave. J. Fluid Mech. 47 (2), 291–304.Google Scholar
Huebner, A., Sharma, S., Srisa-Art, M., Hollfelder, F., Edel, J. B. & deMello, A. J. 2008 Microdroplets: a sea of applications? Lab on a Chip 8 (8), 1244–1254.Google Scholar
Jasak, H., Jemcov, A. & Tukovic, Z. 2007 OpenFOAM: a C++ library for complex physics simulations. In International Workshop on Coupled Methods in Numerical Dynamics, vol. 1000, pp. 1–20. IUC Dubrovnik.Google Scholar
Laser, D. J. & Santiago, J. G. 2004 A review of micropumps. J. Micromech. Microengng 14 (6), R35–R64.Google Scholar
Mao, W., Oron, A. & Alexeev, A. 2013 Fluid transport in thin liquid films using traveling thermal waves. Phys. Fluids 25 (7), 072101.CrossRefGoogle Scholar
Mihaljan, J. M. 1962 A rigorous exposition of the Boussinesq approximations applicable to a thin layer of fluid. Astrophys. J. 136, 1126.Google Scholar
Reyes, D. R., Iossifidis, D., Auroux, P. A. & Manz, A. 2002 Micro total analysis systems. Part 1. Introduction, theory, and technology. Analyt. Chem. 74 (12), 2623–2636.Google Scholar
Schubert, G. & Whitehead, J. A. 1969 Moving flame experiment with liquid mercury: possible implications for the Venus atmosphere. Science 163 (3862), 71–72.Google Scholar
Schubert, G., Young, R. E. & Hinch, J. 1971 Prograde and retrograde motion in a fluid layer: consequences for thermal diffusion in the Venus atmosphere. J. Geophys. Res. 76 (9), 2126–2130.Google Scholar
Song, H., Chen, D. L. & Ismagilov, R. F. 2006 Reactions in droplets in microfluidic channels. Angew. Chem. Intl Ed. Engl. 45 (44), 7336–7356.CrossRefGoogle ScholarPubMed
Stern, M. E. 1959 The moving flame experiment. Tellus 11 (2), 175–179.Google Scholar
Stone, H. A., Stroock, A. D. & Ajdari, A. 2004 Engineering flows in small devices: microfluidics toward a lab-on-a-chip. Annu. Rev. Fluid Mech. 36 (1), 381–411.Google Scholar
Teh, S. Y., Lin, R., Hung, L. H. & Lee, A. P. 2008 Droplet microfluidics. Lab on a Chip 8 (2), 198–220.Google Scholar
Weinert, F., Kraus, J., Franosch, T. & Braun, D. 2008 Microscale fluid flow induced by thermoviscous expansion along a traveling wave. Phys. Rev. Lett. 100 (16), 164501.Google Scholar
Whitehead, J. A. 1972 Observations of rapid mean flow produced in mercury by a moving heater. Geophys. Fluid Dyn. 3 (1), 161–180.Google Scholar
Yariv, E. & Brenner, H. 2004 Flow animation by unsteady temperature fields. Phys. Fluids 16 (11), L95.Google Scholar
Young, R. E., Schubert, G. & Torrance, K. E. 1972 Nonlinear motions induced by moving thermal waves. J. Fluid Mech. 54 (1), 163–187.CrossRefGoogle Scholar
Zhang, C.2017 Computational studies on fluid and particle dynamics. LSU Doctoral Dissertations, 4221.Google Scholar