Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-29T04:46:42.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotic analysis for the propagation and arresting process of a finite dry granular mass down a rough incline

Published online by Cambridge University Press:  30 September 2016

K.-L. Lee  and
F.-L. Yang
K.-L. Lee
Affiliation:
Department of Mechanical Engineering, National Taiwan University, Taipei 10617, Taiwan
F.-L. Yang*
Affiliation:
Department of Mechanical Engineering, National Taiwan University, Taipei 10617, Taiwan
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work presents an asymptotic analysis for the propagation and arresting process of a two-dimensional finite granular mass down a rough incline in a shallow configuration. Bulk shear stress and arresting mechanism are formulated according to the coherence length model that considers momentum transport at a length scale over which grains are spatially correlated. A Bagnold-like streamwise velocity and a non-zero transverse velocity are solved and integrated into a surface kinematic condition to give an advection–diffusion equation for the bulk surface profile, 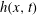$h(x,t)$, that is solved using the matched asymptotic method. These flow solutions are further employed to determine composite solutions for a flow-front trajectory and a local coherence length, 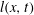$l(x,t)$, which reveals smooth growth of 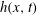$h(x,t)$ and 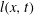$l(x,t)$ from zero at the propagating front with 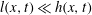$l(x,t)\ll h(x,t)$. At the rear, 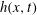$h(x,t)$ vanishes but 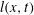$l(x,t)$ asymptotes to a constant that depends on inclination angle. According to the arresting mechanism, the location where 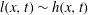$l(x,t)\sim h(x,t)$ is solved to the leading order to locate the deposition front so that its propagation dynamics can be derived. A finite flow arrest time, 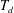$T_{d}$, and the corresponding finite run-out distance, 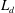$L_{d}$, are evaluated when all the flowing mass has passed the deposition front and are employed to construct a modified front trajectory with the deposition effect. The predicted run-out distance and front trajectory profile compare reasonably well with experimental data in the literature on inclinations at angles higher than the material repose angle.

JFM classification

Geophysical and Geological Flows: Geophysical and Geological Flows Granular media: Granular media Geophysical and Geological Flows: Shallow water flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 806 , 10 November 2016 , pp. 234 - 253
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ancey, C., Cochard, S. & Andreini, N. 2009 The dam-break problem for viscous fluids in the high-capillary-number limit. J. Fluid Mech. 624, 1–22.Google Scholar
Andreotti, B., Forterre, Y. & Pouliquen, O. 2013 Granular Media: Between Fluid and Solid. Cambridge University Press.Google Scholar
Aranson, I. S. & Tsimring, L. S. 2002 Continuum theory of partially fluidized granular flows. Phys. Rev. E 65, 061303.Google ScholarPubMed
Aranson, I. S., Tsimring, L. S., Malloggi, F. & Clément, E. 2008 Nonlocal rheological properties of granular flows near a jamming limit. Phys. Rev. E 78, 031303.Google Scholar
Bagnold, R. A. 1954 Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. Proc. R. Soc. Lond. A 225 (1160), 49–63.Google Scholar
Balmforth, N. J. & Kerswell, R. R. 2005 Granular collapse in two dimensions. J. Fluid Mech. 538, 399–428.CrossRefGoogle Scholar
Baran, O., Ertaş, D., Halsey, T. C., Grest, G. S. & Lechman, J. B. 2006 Velocity correlations in dense gravity-driven granular chute flow. Phys. Rev. E 74, 051302.Google Scholar
Borzsonyi, T., Halsey, T. C. & Ecke, R. E. 2008 Avalanche dynamics on a rough inclined plane. Phys. Rev. E 78, 011306.Google Scholar
Bouchaud, J. P., Cates, M., Prakash, J. R. & Edwards, S. F. 1994 A model for the dynamics of sandpile surfaces. J. Phys. (Paris) I 4, 1383–1410.Google Scholar
Boutreux, T., Raphael, E. & de Gennes, P. G. 1998 Surface flows of granular materials: a modified picture for thick avalanches. Phys. Rev. E 58, 4692–4700.Google Scholar
Bouzid, M., Trulsson, M., Claudin, P., Clément, E. & Andreotti, B. 2013 Nonlocal rheology of granular flows across yield conditions. Phys. Rev. Lett. 111, 238301.Google Scholar
Daerr, A. 2001 Dynamical equilibrium of avalanches on a rough plane. Phys. Fluids 13, 2115–2124.CrossRefGoogle Scholar
Daerr, A. & Douady, S. 1999 Two types of avalanche behaviour in granular media. Nature 399, 241–243.CrossRefGoogle Scholar
Domnik, B. & Pudasaini, S. P. 2012 Full two-dimensional rapid chute flows of simple viscoplastic granular materials with pressure-dependent dynamic slip-velocity and their numerical simulations. J. Non-Newtonian Fluid Mech. 173, 72–86.Google Scholar
Domnik, B., Pudasaini, S. P., Katzenbach, R. & Miller, S. A. 2013 Coupling of full two-dimensional and depth-averaged models for granular flows. J. Non-Newtonian Fluid Mech. 201, 56–68.CrossRefGoogle Scholar
Edwards, A. N. & Gray, J. M. N. T. 2014 Erosion–deposition waves in shallow granular free-surface flows. J. Fluid Mech. 762, 35–37.CrossRefGoogle Scholar
Ertas, D. & Halsey, T. C. 2002 Granular gravitational collapse and chute flow. Eur. Phys. Lett. 60, 931–937.Google Scholar
GDRMidi 2004 On dense granular flows. Eur. Phys. J. E 14, 341–365.Google Scholar
Gray, J. M. N. T. & Ancey, C. 2009 Segregation, recirculation and deposition of coarse particles near two-dimensional avalanche fronts. J. Fluid Mech. 629, 387–423.CrossRefGoogle Scholar
Gray, J. M. N. T. & Edwards, A. N. 2014 A depth-averaged 𝜇(I)-rheology for shallow granular free-surface flows. J. Fluid Mech. 755, 503–534.CrossRefGoogle Scholar
Gray, J. M. N. T., Wieland, M. & Hutter, K. 1999 Gravity-driven free surface flow of granular avalanches over complex basal topography. Phil. Trans. R. Soc. Lond. A 455 (1985), 1841–1874.Google Scholar
Hogg, A. J. 2007 Two dimensional granular slumps down slopes. Phys. Fluids 19, 093301.Google Scholar
Huang, X. & Garcia, M. H. 1998 A Herschel–Bulkley model for mud flow down a slope. J. Fluid Mech. 374, 305–333.Google Scholar
Hunt, B. 1994 Newtonian fluid mechanics treatment of debris flows and avalanches. J. Hydraul. Engng ASCE 120, 1350–1363.Google Scholar
Iverson, R. M. 1997 The physics of debris flows. Rev. Geophys. 35 (3), 245–296.Google Scholar
Jenkins, J. T. 2006 Dense shearing flows of inelastic disks. Phys. Fluids 18, 103307.CrossRefGoogle Scholar
Kamrin, K. & Henann, D. 2015 Modeling the nonlocal behavior of granular flows down inclines. Soft Matt. 11, 179–185.CrossRefGoogle Scholar
Kamrin, K. & Koval, G. 2012 Nonlocal constitutive relation for steady granular flow. Phys. Rev. Lett. 108, 178301.Google Scholar
Kokelaar, B. P., Graham, R. L., Gray, J. M. N. T. & Vallance, J. W. 2014 Fine-grained linings of leveed channels facilitate runout of granular flows. Earth Planet. Sci. Lett. 385, 172–180.Google Scholar
Kumaran, V. 2008 Dense granular flow down an inclined plane: from kinetic theory to granular dynamics. J. Fluid Mech. 599, 121–168.CrossRefGoogle Scholar
Louge, M. Y. 2003 Model for dense granular flows down bumpy inclines. Phys. Rev. E 67, 061303.Google Scholar
Mangeney-Castelnau, A., Bouchut, F., Vilotte, J. P., Lajeunesse, E., Aubertin, A. & Pirulli, M. 2005 On the use of Saint Venant equations to simulate the spreading of a granular mass. J. Geophys. Res. 110 (B9), B09103.Google Scholar
Mangeney-Castelnau, A., Roche, O., Hungr, O., Mangold, N., Faccanoni, G. & Lucas, A. 2010 Erosion and mobility in granular collapse over sloping beds. J. Geophys. Res. 115 (F3), F03040.Google Scholar
Mills, P., Loggia, D. & Tixier, M. 1999 Model for a stationary dense granular flow along an inclined wall. Eur. Phys. Lett. 45, 733–738.Google Scholar
Pouliquen, O. 1999 Scaling laws in granular flows down rough inclined planes. Phys. Fluids 11, 542–548.Google Scholar
Pouliquen, O. 2004 Velocity correlations in dense granular flows. Phys. Rev. Lett. 93, 248001.Google Scholar
Pouliquen, O. & Forterre, Y. 2002 Friction law for dense granular flows: application to the motion of a mass down a rough inclined plane. J. Fluid Mech. 453, 133–151.Google Scholar
Pouliquen, O. & Forterre, Y. 2009 A non-local rheology for dense granular flows. Phil. Trans. R. Soc. Lond. A 367, 5091–5107.Google ScholarPubMed
Pudasaini, S. P. 2011 Some exact solutions for debris and avalanche flows. Phys. Fluids 23, 043301.Google Scholar
Pudasaini, S. P. & Hutter, K. 2003 Rapid shear flows of dry granular masses down curved and twisted channels. J. Fluid Mech. 495, 193–208.Google Scholar
Pudasaini, S. P. & Hutter, K. 2007 Avalanche Dynamics, Dynamics of Rapid Flows of Dense Granular Avalanches. Springer.Google Scholar
Pudasaini, S. P., Wang, Y. & Hutter, K. 2005 Modelling debris flows down general channels. Nat. Hazards Earth Syst. Sci. 5 (6), 799–819.Google Scholar
Reddy, K. A., Forterre, Y. & Pouliquen, O. 2011 Evidence of mechanically activated processes in slow granular flows. Phys. Rev. Lett. 106, 108301.CrossRefGoogle ScholarPubMed
Savage, S. B. & Hutter, K. 1989 The motion of a finite mass of granular material down a rough incline. J. Fluid Mech. 374, 305–333.Google Scholar
Silbert, L., Landry, J. & Grest, G. 2003 Granular flow down a rough inclined plane: transition between thin and thick piles. Phys. Fluids 15, 1–10.Google Scholar
Staron, L. 2008 Correlated motion in the bulk of dense granular flows. Phys. Rev. E 77, 051304.Google Scholar
Staron, L., Lagre, P.-Y., Josserand, C. & Lhuillier, D. 2010 Flow and jamming of a two-dimensional granular bed: toward a nonlocal rheology? Phys. Fluids 22 (11), 113303.CrossRefGoogle Scholar
Tai, Y. & Kuo, C. Y. 2008 A new model of granular flows over general topography with erosion and deposition. Acta Mechanica 199, 71–96.Google Scholar
Whitham, G. B. 1974 Linear and Nonlinear Waves. Wiley.Google Scholar