Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-03T00:43:47.183Z Has data issue: false hasContentIssue false
  • English
  • Français

Apparent yield stress in rigid fibre suspensions: the role of attractive colloidal interactions

Published online by Cambridge University Press:  05 August 2016

S. Bounoua ,
E. Lemaire ,
J. Férec Open the ORCID record for J. Férec [Opens in a new window] ,
G. Ausias ,
A. Zubarev  and
P. Kuzhir
S. Bounoua
Affiliation:
University of Nice-Sophia Antipolis, CNRS UMR7336, Laboratory of Condensed Matter Physics, Parc Valrose, Nice 06100, France
E. Lemaire
Affiliation:
University of Nice-Sophia Antipolis, CNRS UMR7336, Laboratory of Condensed Matter Physics, Parc Valrose, Nice 06100, France
J. Férec
Affiliation:
Institut de Recherche Dupuy de Lôme (IRDL), Univ. Bretagne-Sud, FRE CNRS 3744, IRDL, F-56100 Lorient, France
G. Ausias
Affiliation:
Institut de Recherche Dupuy de Lôme (IRDL), Univ. Bretagne-Sud, FRE CNRS 3744, IRDL, F-56100 Lorient, France
A. Zubarev
Affiliation:
Department of Mathematical Physics, Ural Federal University, 51, Prospekt Lenina, Ekaterinburg 620083, Russia
P. Kuzhir*
Affiliation:
University of Nice-Sophia Antipolis, CNRS UMR7336, Laboratory of Condensed Matter Physics, Parc Valrose, Nice 06100, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This work is focused on the modelling of the shear and normal stresses in fibre suspensions that are subjected to a simple shear flow in the presence of short-range lubrication forces, van der Waals and electrostatic forces, as well as solid friction forces between fibres. All of these forces are weighed by the contact probability. The theory is developed for attractive fibres with van der Waals interaction dominating over electrostatic repulsion. The model predicts a simple Bingham law for both the shear stress and the first normal stress difference, with the apparent shear and normal yield stresses proportional to the second and the third power of the particle volume fraction respectively. The model is applied to the experimental data of Rakatekar et al. (Adv. Mater., vol. 21, 2009, pp. 874–878) and Natale et al. (AIChE J., vol. 60, 2014, pp. 1476–1487) on suspensions of carbon nanotubes dispersed in a Newtonian epoxy resin. It reproduces well the quadratic dependence of the apparent yield stress on the particle volume fraction 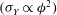$(\unicode[STIX]{x1D70E}_{Y}\propto \unicode[STIX]{x1D719}^{2})$ for average particle aspect ratios of 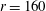$r=160$ and 1200, while it underpredicts the power-law exponent for 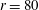$r=80$ (always predicting 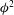$\unicode[STIX]{x1D719}^{2}$ behaviour instead of 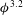$\unicode[STIX]{x1D719}^{3.2}$).

JFM classification

Complex Fluids: Colloids Non-Newtonian Flows: Rheology Complex Fluids: Suspensions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 802 , 10 September 2016 , pp. 611 - 633
Check for updates
Copyright
© 2016 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abisset-Chavanne, E., Chinesta, F., Ferec, J., Ausias, G. & Keunings, R. 2015 On the multiscale description of dilute suspensions of non-Brownian rigid clusters composed of rods. J. Non-Newtonian Fluid Mech. 222, 34–44.Google Scholar
Abisset-Chavanne, E., Mezher, R., Le Corre, S., Ammar, A. & Chinesta, F. 2013 Kinetic theory microstructure modelling in concentrated suspensions. Entropy 15, 2805–2832.Google Scholar
Allaoui, A., Bai, S., Cheng, H. M. & Bai, J. B. 2002 Mechanical and electrical properties of a MWNT/epoxy composite. Compos. Sci. Technol. 62, 1993–1998.Google Scholar
Barnes, H. A. 1999 The yield stress – a review or ‘𝜋𝛼𝜈𝜏𝛼 𝜌𝜀𝜄’ – everything flows? J. Non-Newtonian Fluid Mech. 81, 133–178.Google Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44, 419–440.Google Scholar
Bennington, C. P. J., Kerekes, R. J. & Grace, J. R. 1990 The yield stress of fibre suspensions. Can. J. Chem. Engng 68, 748–757.Google Scholar
Bergström, L. 1998 Shear thinning and shear thickening of concentrated ceramic suspensions. Colloids Surf. A 133, 151–155.Google Scholar
Brenner, H. 1974 Rheology of a dilute suspension of axisymmetric Brownian particles. Intl J. Multiphase Flow 1, 195–341.Google Scholar
Brenner, S. L. & Parsegian, V. A. 1974 A physical method for deriving the electrostatic interaction between rod-like polyions at all mutual angles. Biophys. J. 14, 327–334.Google Scholar
Chaouche, M. & Koch, D. L. 2001 Rheology of non-Brownian rigid fibre suspensions with adhesive contacts. J. Rheol. 45, 369–382.Google Scholar
Christensen, R. M. 1991 Mechanics of Composite Materials. Krieger Publishing Company.Google Scholar
Cui, H. & Grace, J. R. 2007 Flow of pulp fibre suspension and slurries: a review. Intl J. Multiphase Flow 33, 921–934.Google Scholar
Djalili-Moghaddam, M. & Toll, S. 2005 A model for short-range interactions in fibre suspensions. J. Non-Newtonian Fluid Mech. 132, 73–83.Google Scholar
Doi, M. & Edwards, S. F. 1986 The Theory of Polymer Dynamics. Oxford University Press.Google Scholar
Fan, Z. & Advani, S. G. 2007 Rheology of multiwall carbon nanotube suspensions. J. Rheol. 51, 585–604.Google Scholar
Férec, J. & Ausias, G. 2015 Rheological modelling of non-dilute rod suspensions. In Rheology of Non-Spherical Particle Suspensions (ed. Chinesta, F. & Ausias, G.), pp. 77–118. Elsevier.Google Scholar
Férec, J., Ausias, G., Heuzey, M. C. & Carreau, P. J. 2009 Modelling fibre interactions in semiconcentrated fibre suspensions. J. Rheol. 53, 49–72.Google Scholar
Férec, J., Perrot, A. & Ausias, G. 2015 Toward modelling anisotropic yield stress and consistency induced by fibre in fibre-reinforced viscoplastic fluids. J. Non-Newtonian Fluid Mech. 220, 69–76.Google Scholar
Folgar, F. & Tucker, C. L. 1984 Orientation behaviour of fibres in concentrated suspensions. J. Reinf. Plast. Compos. 3, 98–119.Google Scholar
Grossberg, A. Yu. & Khokhlov, A. R. 1981 Statistical theory of polymeric lyotropic liquid crystals. Adv. Polym. Sci. 41, 53–97.Google Scholar
Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52, 683–712.Google Scholar
Hobbie, E. K. 2010 Shear rheology of carbon nanotube suspensions. Rheol. Acta 49, 323–334.Google Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Khalkhal, F., Carreau, P. J. & Ausias, G. 2011 Effect of flow history on linear viscoelastic properties and the evolution of the structure of multiwalled carbon nanotube suspensions in an epoxy. J. Rheol. 55, 153–175.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1987 Course of Theoretical Physics, Vol. 6: Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Larson, R. G. 1999 The Structure and Rheology of Complex Fluids. Oxford University Press.Google Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46, 685–703.Google Scholar
Ma, W. K. A., Chinesta, F., Ammar, A. & Mackley, M. R. 2008 Rheological modelling of carbon nanotube aggregate suspensions. J. Rheol. 52, 1311–1330.CrossRefGoogle Scholar
Michot, L. J., Baravian, C., Bihannic, I., Maddi, S., Moyne, C., Duval, J. F., Levitz, P. & Davidson, P. 2008 Sol–gel and isotropic/nematic transitions in aqueous suspensions of natural nontronite clay. Influence of particle anisotropy. 2. Gel structure and mechanical properties. Langmuir 25, 127–139.Google Scholar
Mongruel, A. & Cloitre, M. 1999 Shear viscosity of suspensions of aligned non-Brownian fibres. Rheol. Acta 38, 451–457.Google Scholar
Mueller, S., Llewellin, E. W. & Mader, H. M. 2010 The rheology of suspensions of solid particles. Proc. R. Soc. Lond. A 466, 1201–1228.Google Scholar
Natale, G., Heuzey, M. C., Carreau, P. J., Ausias, G. & Férec, J. 2014 Rheological modelling of carbon nanotube suspensions with rod–rod interactions. AIChE J. 60, 1476–1487.Google Scholar
Natale, G., Reddy, N. K., Ausias, G., Férec, J., Heuzey, M. C. & Carreau, P. J. 2015 Rheo-optical response of carbon nanotube suspensions. J. Rheol. 59, 499–524.Google Scholar
Petrich, M. P. & Koch, D. L. 1998 Interactions between contacting fibres. Phys. Fluids 10, 2111–2113.Google Scholar
Petrie, C. J. 1999 The rheology of fibre suspensions. J. Non-Newtonian Fluid Mech. 87, 369–402.Google Scholar
Pokrovskiy, V. N. 1978 Statistical Mechanics of Diluted Suspensions. Nauka (in Russian).Google Scholar
Rahatekar, S. S., Koziol, K. K., Kline, S. R., Hobbie, E. K., Gilman, J. W. & Windle, A. H. 2009 Length-dependent mechanics of carbon-nanotube networks. Adv. Mater. 21, 874–878.CrossRefGoogle Scholar
Rahatekar, S. S., Koziol, K. K. K., Butler, S. A., Elliott, J. A., Shaffer, M. S. P., Mackley, M. R. & Windle, A. H. 2006 Optical microstructure and viscosity enhancement for an epoxy resin matrix containing multiwall carbon nanotubes. J. Rheol. 50, 599–610.Google Scholar
Russell, W. B., Saville, D. A. & Schowalter, W. R. 1989 Colloidal Dispersions. Cambridge University Press.Google Scholar
Saarinen, T., Haavisto, S., Sorvari, A., Salmela, J. & Seppälä, J. 2014 The effect of wall depletion on the rheology of microfibrillated cellulose water suspensions by optical coherence tomography. Cellulose 21, 1261–1275.Google Scholar
Schmid, C. F. & Klingenberg, D. J. 2000 Mechanical flocculation in flowing fiber suspensions. Phys. Rev. Lett. 84, 290–293.Google Scholar
Servais, C., Månson, J. A. E. & Toll, S. 1999 Fibre–fibre interaction in concentrated suspensions: disperse fibres. J. Rheol. 43, 991–1004.Google Scholar
Solomon, M. J. & Boger, D. V. 1998 The rheology of aqueous dispersions of spindle-type colloidal hematite rods. J. Rheol. 42, 929–949.Google Scholar
Song, Y. S. & Youn, J. R. 2005 Influence of dispersion states of carbon nanotubes on physical properties of epoxy nanocomposites. Carbon 43, 1378–1385.Google Scholar
Switzer, L. H. & Klingenberg, D. J. 2004 Flocculation in simulations of sheared fibre suspensions. Intl J. Multiphase Flow 30, 67–87.Google Scholar
Toll, S. & Månson, J. A. E. 1994 Dynamics of a planar concentrated fibre suspension with non-hydrodynamic interaction. J. Rheol. 38, 985–997.Google Scholar
Van der Schoot, P. & Odijk, T. 1992 Statistical theory and structure factor of a semidilute solution of rodlike macromolecules interacting by van der Waals forces. J. Chem. Phys. 97, 515–524.Google Scholar
Wierenga, A., Philipse, A. P., Lekkerkerker, H. N. & Boger, D. V. 1998 Aqueous dispersions of colloidal boehmite: structure, dynamics, and yield stress of rod gels. Langmuir 14, 55–65.Google Scholar
Wolf, B., White, D., Melrose, J. R. & Frith, W. J. 2007 On the behaviour of gelled fibre suspensions in steady shear. Rheol. Acta 46, 531–537.Google Scholar
Yamane, Y., Kaneda, Y. & Doi, M. 1994 Numerical simulations of semi-dilute suspensions of rodlike particles in shear flow. J. Non-Newtonian Fluid Mech. 54, 405–421.Google Scholar