Article contents
Analysis of the forward and backward in time pair-separation probability density functions for inertial particles in isotropic turbulence
Published online by Cambridge University Press: 29 September 2017
Abstract
In this paper we investigate, using theory and direct numerical simulations (DNS), the forward in time (FIT) and backward in time (BIT) probability density functions (PDFs) of the separation of inertial particle pairs in isotropic turbulence. In agreement with our earlier study (Bragg et al., Phys. Fluids, vol. 28, 2016, 013305), where we compared the FIT and BIT mean-square separations, we find that inertial particles separate much faster BIT than FIT, with the strength of the irreversibility depending upon the final/initial separation of the particle pair and their Stokes number 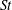 $St$. However, we also find that the irreversibility shows up in subtle ways in the behaviour of the full PDF that it does not in the mean-square separation. In the theory, we derive new predictions, including a prediction for the BIT/FIT PDF for
$St$. However, we also find that the irreversibility shows up in subtle ways in the behaviour of the full PDF that it does not in the mean-square separation. In the theory, we derive new predictions, including a prediction for the BIT/FIT PDF for 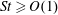 $St\geqslant O(1)$, and for final/initial separations in the dissipation regime. The prediction shows how caustics in the particle relative velocities in the dissipation range affect the scaling of the pair-separation PDF, leading to a PDF with an algebraically decaying tail. The predicted functional behaviour of the PDFs is universal, in that it does not depend upon the level of intermittency in the underlying turbulence. We also analyse the pair-separation PDFs for fluid particles at short times, and construct theoretical predictions using the multifractal formalism to describe the fluid relative velocity distributions. The theoretical and numerical results both suggest that the extreme events in the inertial particle-pair dispersion at the small scales are dominated by their non-local interaction with the turbulent velocity field, rather than due to the strong dissipation range intermittency of the turbulence itself. In fact, our theoretical results predict that for final/initial separations in the dissipation range, when
$St\geqslant O(1)$, and for final/initial separations in the dissipation regime. The prediction shows how caustics in the particle relative velocities in the dissipation range affect the scaling of the pair-separation PDF, leading to a PDF with an algebraically decaying tail. The predicted functional behaviour of the PDFs is universal, in that it does not depend upon the level of intermittency in the underlying turbulence. We also analyse the pair-separation PDFs for fluid particles at short times, and construct theoretical predictions using the multifractal formalism to describe the fluid relative velocity distributions. The theoretical and numerical results both suggest that the extreme events in the inertial particle-pair dispersion at the small scales are dominated by their non-local interaction with the turbulent velocity field, rather than due to the strong dissipation range intermittency of the turbulence itself. In fact, our theoretical results predict that for final/initial separations in the dissipation range, when 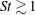 $St\gtrsim 1$, the tails of the pair-separation PDFs decay faster as the Taylor Reynolds number
$St\gtrsim 1$, the tails of the pair-separation PDFs decay faster as the Taylor Reynolds number 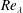 $Re_{\unicode[STIX]{x1D706}}$ is increased, the opposite of what would be expected for fluid particles.
$Re_{\unicode[STIX]{x1D706}}$ is increased, the opposite of what would be expected for fluid particles.
- Type
- Papers
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 9
- Cited by



