Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T08:26:49.795Z Has data issue: false hasContentIssue false
  • English
  • Français

Amplification and structure of streamwise-velocity fluctuations in compression-corner shock-wave/turbulent boundary-layer interactions

Published online by Cambridge University Press:  31 January 2019

M. A. Mustafa Open the ORCID record for M. A. Mustafa [Opens in a new window] ,
N. J. Parziale Open the ORCID record for N. J. Parziale [Opens in a new window] ,
M. S. Smith  and
E. C. Marineau
M. A. Mustafa
Affiliation:
Department of Mechanical Engineering, Stevens Institute of Technology, Hoboken, NJ 07030, USA
N. J. Parziale*
Affiliation:
Department of Mechanical Engineering, Stevens Institute of Technology, Hoboken, NJ 07030, USA
M. S. Smith
Affiliation:
Arnold Engineering Development Complex – White Oak, Silver Spring, MD 20903, USA
E. C. Marineau
Affiliation:
Arnold Engineering Development Complex – White Oak, Silver Spring, MD 20903, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

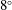In this work, we study the effect of the compression-corner angle on the streamwise turbulent kinetic energy (sTKE) and structure in Mach 2.8 flow. Krypton tagging velocimetry (KTV) is used to investigate the incoming turbulent boundary layer and flow over $8^{\circ }$, 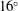$16^{\circ }$, 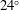$24^{\circ }$ and 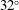$32^{\circ }$ compression corners. The experiments were performed in a 99 % 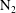$\text{N}_{2}$ and 1 % Kr gas mixture in the Arnold Engineering Development Complex (AEDC) Mach 3 Calibration Tunnel (M3CT) at 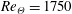$Re_{\unicode[STIX]{x1D6E9}}=1750$. A figure of merit is defined as the wall-normal integrated sTKE ($\overline{\text{sTKE}}$), which is designed to identify turbulence amplification by accounting for the root-mean-squared (r.m.s.) velocity fluctuations and shear-layer width for the different geometries. We observe that the 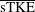$\overline{\text{sTKE}}$ increases as an exponential with the compression-corner angle near the root when normalized by the boundary-layer value. Additionally, snapshot proper orthogonal decomposition (POD) is applied to the KTV results to investigate the structure of the flow. From the POD results, we extract the dominant flow structures and compare each case by presenting mean-velocity maps that correspond to the largest positive and negative POD mode coefficients. Finally, the POD spectrum reveals an inertial range common to the boundary-layer and each compression-corner flow that is present after the first 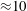${\approx}10$ dominant POD modes.

JFM classification

Aerodynamics: High-speed flow Compressible Flows: Shock waves Turbulent Flows: Turbulent boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 863 , 25 March 2019 , pp. 1091 - 1122
Copyright
© Cambridge University Press 2019. This is a work of the U.S. Government and is not subject to copyright protection in the United States. 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adams, N. A. 2000 Direct simulation of the turbulent boundary layer along a compression ramp at m = 3 and re𝛩 = 1685. J. Fluid Mech. 420, 47–83.10.1017/S0022112000001257Google Scholar
André, M. A., Bardet, P. M., Burns, R. A. & Danehy, P. M. 2017 Characterization of hydroxyl tagging velocimetry for low-speed flows. Meas. Sci. Technol. 28 (8), 085202.10.1088/1361-6501/aa7ac8Google Scholar
André, M. A., Burns, R. A., Danehy, P. M., Cadell, S. R., Woods, B. G. & Bardet, P. M. 2018 Development of N2O‐MTV for low-speed flow and in-situ deployment to an integral effect test facility. Exp. Fluids 59 (1), 14.10.1007/s00348-017-2470-3Google Scholar
Babinsky, H. & Harvey, J. K.(Eds) 2011 Shock Wave-Boundary-Layer Interactions, 1st edn. Cambridge University Press.10.1017/CBO9780511842757Google Scholar
Balla, R. J. 2013 Iodine tagging velocimetry in a Mach 10 wake. AIAA J. 51 (7), 1–3.10.2514/1.J052416Google Scholar
Balla, R. J. & Everhart, J. L. 2012 Rayleigh scattering density measurements, cluster theory, and nucleation calculations at Mach 10. AIAA J. 50 (3), 698–707.10.2514/1.J051334Google Scholar
Barker, P., Bishop, A. & Rubinsztein-Dunlop, H. 1997 Supersonic velocimetry in a shock tube using laser enhanced ionisation and planar laser induced fluorescence. Appl. Phys. B 64 (3), 369–376.10.1007/s003400050186Google Scholar
Bathel, B. F., Danehy, P. M., Inman, J. A., Jones, S. B., Ivey, C. B. & Goyne, C. P. 2011 Velocity profile measurements in hypersonic flows using sequentially imaged fluorescence-based molecular tagging. AIAA J. 49 (9), 1883–1896.10.2514/1.J050722Google Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.10.1146/annurev.fl.25.010193.002543Google Scholar
Boedeker, L. R. 1989 Velocity measurement by H2O photolysis and laser-induced fluorescence of OH. Opt. Lett. 14 (10), 473–475.10.1364/OL.14.000473Google Scholar
Bonnet, J. P., Cole, D. R., Delville, J., Glauser, M. N. & Ukeiley, L. S. 1994 Stochastic estimation and proper orthogonal decomposition: complementary techniques for identifying structure. Exp. Fluids 17 (5), 307–314.10.1007/BF01874409Google Scholar
Bradshaw, P. 1977 Compressible turbulent shear layers. Annu. Rev. Fluid Mech. 9 (1), 33–52.10.1146/annurev.fl.09.010177.000341Google Scholar
Brooks, J., Gupta, A., Smith, M. S. & Marineau, E. C. 2014 Development of non-intrusive velocity measurement capabilities at AEDC tunnel 9. In Proceedings of 52nd Aerospace Sciences Meeting, SciTech. National Harbor, Maryland. AIAA-2014-1239.Google Scholar
Brooks, J. M., Gupta, A. K., Smith, M. S. & Marineau, E. C. 2015 Development of particle image velocimetry in a Mach 2.7 wind tunnel at AEDC White Oak. In Proceedings of 53nd Aerospace Sciences Meeting, SciTech. Kissimmee, Florida. AIAA-2015-1915.Google Scholar
Brooks, J. M., Gupta, A. K., Smith, M. S. & Marineau, E. C. 2016 PIV measurements of Mach 2.7 turbulent boundary layer with varying Reynolds numbers. In Proceedings of 54th Aerospace Sciences Meeting, SciTech. San Diego, California. AIAA-2016-1147.Google Scholar
Brooks, J. M., Gupta, A. K., Smith, M. S. & Marineau, E. C. 2018 Particle image velocimetry measurements of Mach 3 turbulent boundary layers at low Reynolds numbers. Exp. Fluids 59 (3), 83.10.1007/s00348-018-2536-xGoogle Scholar
Chang, R. S. F., Horiguchi, H. & Setser, D. W. 1980 Radiative lifetimes and twobody collisional deactivation rate constants in argon for Kr(4p55p) and Kr(4p55p) states. J. Chem. Phys. 73 (2), 778–790.10.1063/1.440185Google Scholar
Chen, H., Reuss, D. L., Hung, D. L. S. & Sick, V. 2013 A practical guide for using proper orthogonal decomposition in engine research. Intl J. Engine Res. 14 (4), 307–319.10.1177/1468087412455748Google Scholar
Chen, H., Reuss, D. L. & Sick, V. 2012 On the use and interpretation of proper orthogonal decomposition of in-cylinder engine flows. Meas. Sci. Technol. 23 (8), 085302.10.1088/0957-0233/23/8/085302Google Scholar
Clemens, N. T. & Narayanaswamy, V. 2014 Low-frequency unsteadiness of shock wave/turbulent boundary layer interactions. Annu. Rev. Fluid Mech. 46, 469–492.10.1146/annurev-fluid-010313-141346Google Scholar
Dam, N., Klein-Douwel, R. J. H., Sijtsema, N. M. & ter Meulen, J. J. 2001 Nitric oxide flow tagging in unseeded air. Opt. Lett. 26 (1), 36–38.10.1364/OL.26.000036Google Scholar
Dolling, D. S. 2001 Fifty years of shock-wave/boundary-layer interaction research: What next?. AIAA J. 39 (8), 1517–1531.10.2514/2.1476Google Scholar
Druault, P., Guibert, P. & Alizon, F. 2005 Use of proper orthogonal decomposition for time interpolation from PIV data. Exp. Fluids 39 (6), 1009–1023.10.1007/s00348-005-0035-3Google Scholar
Duan, L, Beekman, I & Martin, M. P. 2011 Direct numerical simulation of hypersonic turbulent boundary layers. Part 3. Effect of Mach number. J. Fluid Mech. 672, 245–267.10.1017/S0022112010005902Google Scholar
Edwards, M. R., Dogariu, A. & Miles, R. B. 2015 Simultaneous temperature and velocity measurements in air with femtosecond laser tagging. AIAA J. 53 (8), 2280–2288.10.2514/1.J053685Google Scholar
Elena, M., Lacharme, J. P. & Gaviglio, J. 1985 Comparison of hot-wire and laser Doppler anemometry methods in supersonic turbulent boundary layers. In Proceedings of 2nd International Symposium on Laser Anemometry, pp. 151–157.Google Scholar
Gaitonde, D. V. 2015 Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 72, 80–99.10.1016/j.paerosci.2014.09.002Google Scholar
Gendrich, C. P. & Koochesfahani, M. M. 1996 A spatial correlation technique for estimating velocity fields using molecular tagging velocimetry (MTV). Exp. Fluids 22 (1), 67–77.10.1007/BF01893307Google Scholar
Gendrich, C. P., Koochesfahani, M. M. & Nocera, D. G. 1997 Molecular tagging velocimetry and other novel applications of a new phosphorescent supramolecule. Exp. Fluids 23 (5), 361–372.10.1007/s003480050123Google Scholar
Giepman, R. H. M., Schrijer, F. F. J. & van Oudheusden, B. W. 2015 High-resolution PIV measurements of a transitional shock wave-boundary layer interaction. Exp. Fluids 56 (6), 113.10.1007/s00348-015-1977-8Google Scholar
Haertig, J., Havermann, M., Rey, C. & George, A. 2002 Particle image velocimetry in Mach 3.5 and 4.5 shock-tunnel flows. AIAA J. 40 (6), 1056–1060.10.2514/2.1787Google Scholar
Handa, T., Mii, K., Sakurai, T., Imamura, K., Mizuta, S. & Ando, Y. 2014 Study on supersonic rectangular microjets using molecular tagging velocimetry. Exp. Fluids 55 (5), 1–9.10.1007/s00348-014-1725-5Google Scholar
Helm, C., Martin, M. P. & Dupont, P. 2014 Characterization of the shear layer in a Mach 3 shock/turbulent boundary layer interaction. J Phys.: Conf. Ser. 506 (1), 012013.Google Scholar
Hill, R. B. & Klewicki, J. C. 1996 Data reduction methods for flow tagging velocity measurements. Exp. Fluids 20 (3), 142–152.10.1007/BF00190270Google Scholar
Hiller, B., Booman, R. A., Hassa, C. & Hanson, R. K. 1984 Velocity visualization in gas flows using laser-induced phosphorescence of biacetyl. Rev. Sci. Instrum. 55 (12), 1964–1967.10.1063/1.1137687Google Scholar
Hsu, A. G., Srinivasan, R., Bowersox, R. D. W. & North, S. W. 2009a Molecular tagging using vibrationally excited nitric oxide in an underexpanded jet flowfield. AIAA J. 47 (11), 2597–2604.10.2514/1.39998Google Scholar
Hsu, A. G., Srinivasan, R., Bowersox, R. D. W. & North, S. W. 2009b Two-component molecular tagging velocimetry utilizing NO fluorescence lifetime and NO2 photodissociation techniques in an underexpanded jet flowfield. Appl. Opt. 48 (22), 4414–4423.10.1364/AO.48.004414Google Scholar
Huang, P. G. & Coleman, G. N. 1994 Van driest transformation and compressible wall-bounded flows. AIAA J. 32 (10), 2110–2113.Google Scholar
Humble, R. A., Elsinga, G. E., Scarano, F. & van Oudheusden, B. W. 2009 Three-dimensional instantaneous structure of a shock wave/turbulent boundary layer interaction. J. Fluid Mech. 622, 33–62.10.1017/S0022112008005090Google Scholar
Humble, R. A., Scarano, F. & van Oudheusden, B. W. 2007 Particle image velocimetry measurements of a shock wave/turbulent boundary layer interaction. Exp. Fluids 43 (2–3), 173–183.10.1007/s00348-007-0337-8Google Scholar
Jiang, N., Halls, B. R., Stauffer, H. U., Danehy, P. M., Gord, J. R. & Roy, S. 2016 Selective two-photon absorptive resonance femtosecond-laser electronic-excitation tagging velocimetry. Opt. Lett. 41 (10), 2225–2228.10.1364/OL.41.002225Google Scholar
Jiang, N., Mance, J. G., Slipchenko, M. N., Felver, J. J., Stauffer, H. U., Yi, T., Danehy, P. M. & Roy, S. 2017 Seedless velocimetry at 100 kHz with picosecond-laser electronic-excitation tagging. Opt. Lett. 42 (2), 239–242.10.1364/OL.42.000239Google Scholar
John, B., Kulkarni, V. N. & Natarajan, G. 2014 Shock wave boundary layer interactions in hypersonic flows. Intl J. Heat Mass Transfer 70, 81–90.10.1016/j.ijheatmasstransfer.2013.10.072Google Scholar
von Kármán, T. 1934 Turbulence and skin friction. J. Aeronaut. Sci. 1 (1), 1–20.10.2514/8.5Google Scholar
Klebanoff, P. S.1955 Characteristics of turbulence in a boundary layer with zero pressure gradient. NACA TR-1247.Google Scholar
Knight, B. & Sirovich, L. 1990 Kolmogorov inertial range for inhomogeneous turbulent flows. Phys. Rev. Lett. 65 (11), 1356–1359.10.1103/PhysRevLett.65.1356Google Scholar
Knight, D., Yan, H., Panaras, A. G. & Zheltovodov, A. 2003 Advances in CFD prediction of shock wave turbulent boundary layer interactions. Prog. Aerosp. Sci. 39 (2), 121–184.10.1016/S0376-0421(02)00069-6Google Scholar
Kolmogorov, A. N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Proc. R. Soc. Lond. A 30 (4), 299–303.Google Scholar
Lempert, W. R., Boehm, M., Jiang, N., Gimelshein, S. & Levin, D. 2003 Comparison of molecular tagging velocimetry data and direct simulation Monte Carlo simulations in supersonic micro jet flows. Exp. Fluids 34 (3), 403–411.10.1007/s00348-002-0576-7Google Scholar
Lempert, W. R., Jiang, N., Sethuram, S. & Samimy, M. 2002 Molecular tagging velocimetry measurements in supersonic microjets. AIAA J. 40 (6), 1065–1070.10.2514/2.1789Google Scholar
Loth, E. 2008 Compressibility and rarefaction effects on drag of a spherical particle. AIAA J. 46 (9), 2219–2228.10.2514/1.28943Google Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation (ed. Yaglom, A. M. & Tatarsky, V. I.), pp. 166–176. Nauka Press.Google Scholar
Martin, M. P. 2007 Direct numerical simulation of hypersonic turbulent boundary layers. Part 1. Initialization and comparison with experiments. J. Fluid Mech. 570, 347–364.10.1017/S0022112006003107Google Scholar
McDaniel, J. C., Hiller, B. & Hanson, R. K. 1983 Simultaneous multiple-point velocity measurements using laser-induced iodine fluorescence. Opt. Lett. 8 (1), 51–53.10.1364/OL.8.000051Google Scholar
Michael, J. B., Edwards, M. R., Dogariu, A. & Miles, R. B. 2011 Femtosecond laser electronic excitation tagging for quantitative velocity imaging in air. Appl. Opt. 50 (26), 5158–5162.10.1364/AO.50.005158Google Scholar
Miles, R., Cohen, C., Connors, J., Howard, P., Huang, S., Markovitz, E. & Russell, G. 1987 Velocity measurements by vibrational tagging and fluorescent probing of oxygen. Opt. Lett. 12 (11), 861–863.10.1364/OL.12.000861Google Scholar
Miles, R. B., Connors, J. J., Markovitz, E. C., Howard, P. J. & Roth, G. J. 1989 Instantaneous profiles and turbulence statistics of supersonic free shear layers by Raman excitation plus laser-induced electronic fluorescence (RELIEF) velocity tagging of oxygen. Exp. Fluids 8 (1–2), 17–24.10.1007/BF00203060Google Scholar
Miles, R. B., Grinstead, J., Kohl, R. H. & Diskin, G. 2000 The RELIEF flow tagging technique and its application in engine testing facilities and for helium-air mixing studies. Meas. Sci. Technol. 11 (9), 1272–1281.10.1088/0957-0233/11/9/304Google Scholar
Miles, R. B. & Lempert, W. R. 1997 Quantitative flow visualization in unseeded flows. Annu. Rev. Fluid Mech. 29 (1), 285–326.10.1146/annurev.fluid.29.1.285Google Scholar
Miles, R. B., Zhou, D., Zhang, B. & Lempert, W. R. 1993 Fundamental turbulence measurements by RELIEF flow tagging. AIAA J. 31 (3), 447–452.10.2514/3.11350Google Scholar
Mills, J. L.2016 Investigation of multi-photon excitation in argon with applications in hypersonic flow diagnostics. PhD thesis, Old Dominion University.Google Scholar
Mills, J. L., Sukenik, C. I. & Balla, R. J. 2011 Hypersonic wake diagnostics using laser induced fluorescence techniques. In Proceedings of 42nd AIAA Plasmadynamics and Lasers Conference, Honolulu, Hawaii. AIAA 2011-3459.Google Scholar
Morkovin, M. V. 1962 Effects of compressibility on turbulent flows. In Mécanique de la Turbulence, pp. 367–380. CNRS.Google Scholar
Moser, R. D. 1994 Kolmogorov inertial range spectra for inhomogeneous turbulence. Phys. Fluids 6 (2), 794–801.10.1063/1.868317Google Scholar
Murray, N., Sällström, E. & Ukeiley, L. 2009 Properties of subsonic open cavity flow fields. Phys. Fluids 21 (9), 095103.10.1063/1.3210772Google Scholar
Mustafa, M. A., Hunt, M. B., Parziale, N. J., Smith, M. S. & Marineau, E. C. 2017a Krypton tagging velocimetry (KTV) investigation of shock-wave/turbulent boundary-layer interaction. In Proceedings of AIAA SciTech 2017. Grapevine, Texas. AIAA-2017-0025.Google Scholar
Mustafa, M. A. & Parziale, N. J. 2017 Krypton tagging velocimetry in the stevens shock tube. In Proceedings of 33rd AIAA Aerodynamic Measurement Technology and Ground Testing Conference. Denver, Colorado. AIAA-2017-3897.Google Scholar
Mustafa, M. A. & Parziale, N. J. 2018 Simplified read schemes for krypton tagging velocimetry in N2 and air. Opt. Lett. 43 (12), 2909–2912.10.1364/OL.43.002909Google Scholar
Mustafa, M. A., Parziale, N. J., Smith, M. S. & Marineau, E. C. 2017b Nonintrusive freestream velocity measurement in a large-scale hypersonic wind tunnel. AIAA J. 55 (10), 3611–3616.10.2514/1.J056177Google Scholar
Mustafa, M. A., Parziale, N. J., Smith, M. S. & Marineau, E. C. 2018 Two-dimensional Krypton Tagging Velocimetry (KTV-2D) investigation of shock-wave/turbulent boundary-layer interaction. In Proceedings of AIAA SciTech 2018. Kissimmee, Florida. AIAA-2018-1771.Google Scholar
O’Haver, T. 1997 A Pragmatic Introduction to Signal Processing. University of Maryland at College Park.Google Scholar
Orellano, A. & Wengle, H. 2001 Pod analysis of coherent structures in forced turbulent flow over a fence. J. Turbul. 2, N8.10.1088/1468-5248/2/1/008Google Scholar
Parziale, N. J., Smith, M. S. & Marineau, E. C. 2015a Krypton tagging velocimetry for use in high-speed ground-test facilities. In Proceedings of AIAA SciTech 2015. Kissimmee, Florida. AIAA-2015-1484.Google Scholar
Parziale, N. J., Smith, M. S. & Marineau, E. C. 2015b Krypton tagging velocimetry of an underexpanded jet. Appl. Opt. 54 (16), 5094–5101.10.1364/AO.54.005094Google Scholar
Piponniau, S., Collin, E., Dupont, P. & Debiève, J. 2012 Reconstruction of velocity fields from wall pressure measurements in a shock wave/turbulent boundary layer interaction. Intl J. Heat Fluid Flow 35, 176–186.10.1016/j.ijheatfluidflow.2012.02.006Google Scholar
Pitz, R. W., Lahr, M. D., Douglas, Z. W., Wehrmeyer, J. A., Hu, S., Carter, C. D., Hsu, K.-Y., Lum, C. & Koochesfahani, M. M. 2005 Hydroxyl tagging velocimetry in a supersonic flow over a cavity. Appl. Opt. 44 (31), 6692–6700.10.1364/AO.44.006692Google Scholar
Porter, K. M. & Poggie, J. 2017 Turbulent structure and large-scale unsteadiness in shock-wave/boundary layer interaction. In Proceedings of AIAA SciTech 2017. Grapevine, Texas. AIAA-2017-0533.Google Scholar
Ribarov, L. A., Wehrmeyer, J. A., Batliwala, F., Pitz, R. W. & DeBarber, P. A. 1999 Ozone tagging velocimetry using narrowband excimer lasers. AIAA J. 37 (6), 708–714.10.2514/2.799Google Scholar
Rowley, C. W., Colonius, T. & Murray, R. M. 2004 Model reduction for compressible flows using pod and galerkin projection. Phys. D 189 (1–2), 115–129.10.1016/j.physd.2003.03.001Google Scholar
Sánchez-González, R., Bowersox, R. D. W. & North, S. W. 2012 Simultaneous velocity and temperature measurements in gaseous flowfields using the vibrationally excited nitric oxide monitoring technique: a comprehensive study. Appl. Opt. 51 (9), 1216–1228.10.1364/AO.51.001216Google Scholar
Sánchez-González, R., Bowersox, R. D. W. & North, S. W. 2014 Vibrationally excited NO tagging by NO(A2𝛴+) fluorescence and quenching for simultaneous velocimetry and thermometry in gaseous flows. Opt. Lett. 39 (9), 2771–2774.10.1364/OL.39.002771Google Scholar
Sánchez-González, R., Srinivasan, R., Bowersox, R. D. W. & North, S. W. 2011 Simultaneous velocity and temperature measurements in gaseous flow fields using the venom technique. Opt. Lett. 36 (2), 196–198.10.1364/OL.36.000196Google Scholar
Schlichting, H. 2000 Boundary-Layer Theory. Springer.10.1007/978-3-642-85829-1Google Scholar
Schoenherr, K. E. 1932 Resistance of flat surfaces moving through a fluid. Trans. Soc. Nav. Archit. Mar. Engrs 40, 279–313.Google Scholar
Settles, G. S. 2001 Schlieren and Shadowgraph Techniques, 1st edn. Springer.10.1007/978-3-642-56640-0Google Scholar
Settles, G. S. & Dodson, L. J.1994 Hypersonic shock/boundary-layer interaction database: new and corrected data. NASA CR 177638.Google Scholar
Settles, G. S., Fitzpatrick, T. J. & Bogdonoff, S. M. 1979 Detailed study of attached and separated compression corner flowfields in high Reynolds number supersonic flow. AIAA J. 17 (6), 579–585.10.2514/3.61180Google Scholar
Settles, G. S., Vas, I. E. & Bogdonoff, S. M. 1976 Details of a shock-separated turbulent boundary layer at a compression corner. AIAA J. 14 (12), 1709–1715.10.2514/3.61513Google Scholar
Sijtsema, N. M., Dam, N. J., Klein-Douwel, R. J. H. & ter Meulen, J. J. 2002 Air photolysis and recombination tracking: A new molecular tagging velocimetry scheme. AIAA J. 40 (6), 1061–1064.10.2514/2.1788Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures, Part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.10.1090/qam/910462Google Scholar
Smits, A. J. & Muck, K.-C. 1987 Experimental study of three shock wave/turbulent boundary layer interactions. J. Fluid Mech. 182, 291–314.10.1017/S0022112087002349Google Scholar
Spaid, F. W. & Frishett, J. C. 1972 Incipient separation of a supersonic, turbulent boundary layer, including effects of heat transfer. AIAA 10 (7), 915–922.10.2514/3.50245Google Scholar
Stier, B. & Koochesfahani, M. M. 1999 Molecular tagging velocimetry (MTV) measurements in gas phase flows. Exp. Fluids 26 (4), 297–304.10.1007/s003480050292Google Scholar
Stöhr, M., Sadanandan, R. & Meier, W. 2011 Phase-resolved characterization of vortex–flame interaction in a turbulent swirl flame. Exp. Fluids 51 (4), 1153–1167.10.1007/s00348-011-1134-yGoogle Scholar
Taira, K., Brunton, S. L., Dawson, S. T. M., Rowley, C. W., Colonius, T., McKeon, B. J., Schmidt, O. T., Gordeyev, S., Theofilis, V. & Ukeiley, L. S. 2017 Modal analysis of fluid flows: an overview. AIAA J. 55 (12), 1–29.10.2514/1.J056060Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Tu, J. H., Rowley, C. W., Kutz, J. N. & Shang, J. K. 2014 Spectral analysis of fluid flows using sub-Nyquist-rate PIV data. Exp. Fluids 55 (9), 1805.10.1007/s00348-014-1805-6Google Scholar
Van der Laan, W. P. N., Tolboom, R. A. L., Dam, N. J. & ter Meulen, J. J. 2003 Molecular tagging velocimetry in the wake of an object in supersonic flow. Exp. Fluids 34 (4), 531–534.10.1007/s00348-003-0593-1Google Scholar
Wang, B., Sandham, N. D., Hu, Z. & Liu, W. 2015 Numerical study of oblique shock-wave/boundary-layer interaction considering sidewall effects. J. Fluid Mech. 767, 526–561.10.1017/jfm.2015.58Google Scholar
Wehrmeyer, J. A., Ribarov, L. A., Oguss, D. A. & Pitz, R. W. 1999 Flame flow tagging velocimetry with 193 nm H2O photodissociation. Appl. Opt. 38 (33), 6912–6917.10.1364/AO.38.006912Google Scholar
Wu, M. & Martin, M. P. 2007 Direct numerical simulation of supersonic turbulent boundary layer over a compression ramp. AIAA J. 45 (4), 879–889.10.2514/1.27021Google Scholar
Wu, M. & Martin, M. P. 2008 Analysis of shock motion in shockwave and turbulent boundary layer interaction using direct numerical simulation data. J. Fluid Mech. 594, 71–83.10.1017/S0022112007009044Google Scholar
Zahradka, D., Parziale, N. J., Smith, M. S. & Marineau, E. C. 2016a Krypton tagging velocimetry in a turbulent Mach 2.7 boundary layer. Exp. Fluids 57, 62.10.1007/s00348-016-2148-2Google Scholar
Zahradka, D., Parziale, N. J., Smith, M. S. & Marineau, E. C. 2016b Krypton tagging velocimetry (KTV) in supersonic turbulent boundary layers. In Proceedings of AIAA SciTech 2016. San Diego, California. AIAA-2016-1587.Google Scholar
Zhang, S., Yu, X., Yan, H., Huang, H. & Liu, H. 2017 Molecular tagging velocimetry of NH fluorescence in a high-enthalpy rarefied gas flow. Appl. Phys. B 123 (4), 122.10.1007/s00340-017-6703-1Google Scholar

Mustafa et al. supplementary movie 1

8 degree corner instantaneous fluorescence exposures and corresponding velocity profiles.

Download Mustafa et al. supplementary movie 1(Video)
Video 6.8 MB

Mustafa et al. supplementary movie 2

16 degree corner instantaneous fluorescence exposures and corresponding velocity profiles.

Download Mustafa et al. supplementary movie 2(Video)
Video 6.5 MB

Mustafa et al. supplementary movie 3

24 degree corner instantaneous fluorescence exposures and corresponding velocity profiles.

Download Mustafa et al. supplementary movie 3(Video)
Video 6.6 MB

Mustafa et al. supplementary movie 4

32 degree corner instantaneous fluorescence exposures and corresponding velocity profiles.

Download Mustafa et al. supplementary movie 4(Video)
Video 7.4 MB