Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Náraigh, Lennon Ó
and
Spelt, Peter D. M.
2013.
An analytical connection between temporal and spatio-temporal growth rates in linear stability analysis.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 469,
Issue. 2156,
p.
20130171.
Fuster, D.
Matas, J.-P.
Marty, S.
Popinet, S.
Hoepffner, J.
Cartellier, A.
and
Zaleski, S.
2013.
Instability regimes in the primary breakup region of planar coflowing sheets.
Journal of Fluid Mechanics,
Vol. 736,
Issue. ,
p.
150.
Lin, Jianzhong
Xia, Yi
and
Bao, Fubing
2014.
Hydrodynamic instability of nanofluids in a channel flow.
Fluid Dynamics Research,
Vol. 46,
Issue. 5,
p.
055512.
Ó Náraigh, Lennon
Valluri, Prashant
Scott, David M.
Bethune, Iain
and
Spelt, Peter D. M.
2014.
Linear instability, nonlinear instability and ligament dynamics in three-dimensional laminar two-layer liquid–liquid flows.
Journal of Fluid Mechanics,
Vol. 750,
Issue. ,
p.
464.
Vellingiri, Rajagopal
Tseluiko, Dmitri
and
Kalliadasis, Serafim
2015.
Absolute and convective instabilities in counter-current gas–liquid film flows.
Journal of Fluid Mechanics,
Vol. 763,
Issue. ,
p.
166.
Thibault, Daniel
Munoz, Jean-Michel
and
Liné, Alain
2015.
Multiple holdup solutions in laminar stratified flow in inclined channels.
International Journal of Multiphase Flow,
Vol. 73,
Issue. ,
p.
275.
Matas, Jean-Philippe
Marty, Sylvain
Dem, Mohamed Seydou
and
Cartellier, Alain
2015.
Influence of Gas Turbulence on the Instability of an Air-Water Mixing Layer.
Physical Review Letters,
Vol. 115,
Issue. 7,
Schmidt, Patrick
Ó Náraigh, Lennon
Lucquiaud, Mathieu
and
Valluri, Prashant
2016.
Linear and nonlinear instability in vertical counter-current laminar gas-liquid flows.
Physics of Fluids,
Vol. 28,
Issue. 4,
Ó Náraigh, Lennon
and
Spelt, Peter D. M.
2018.
Instability of pressure-driven gas–liquid two-layer channel flows in two and three dimensions.
Journal of Fluid Mechanics,
Vol. 849,
Issue. ,
p.
1.
Matas, Jean-Philippe
Delon, Antoine
and
Cartellier, Alain
2018.
Shear instability of an axisymmetric air–water coaxial jet.
Journal of Fluid Mechanics,
Vol. 843,
Issue. ,
p.
575.
Bender, Achim
Stroh, Alexander
Frohnapfel, Bettina
Stephan, Peter
and
Gambaryan-Roisman, Tatiana
2019.
Combined direct numerical simulation and long-wave simulation of a liquid film sheared by a turbulent gas flow in a channel.
Physics of Fluids,
Vol. 31,
Issue. 2,
Lavalle, Gianluca
Li, Yiqin
Mergui, Sophie
Grenier, Nicolas
and
Dietze, Georg F.
2019.
Suppression of the Kapitza instability in confined falling liquid films.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
608.
Ling, Y.
Fuster, D.
Tryggvason, G.
and
Zaleski, S.
2019.
A two-phase mixing layer between parallel gas and liquid streams: multiphase turbulence statistics and influence of interfacial instability.
Journal of Fluid Mechanics,
Vol. 859,
Issue. ,
p.
268.
Jiang, Delin
and
Ling, Yue
2020.
Destabilization of a planar liquid stream by a co-flowing turbulent gas stream.
International Journal of Multiphase Flow,
Vol. 122,
Issue. ,
p.
103121.
Mohamed, Omair A. A.
Dallaston, Michael C.
and
Biancofiore, Luca
2021.
Spatiotemporal evolution of evaporating liquid films sheared by a gas.
Physical Review Fluids,
Vol. 6,
Issue. 11,
Jiang, D.
and
Ling, Y.
2021.
Impact of inlet gas turbulence on the formation, development and breakup of interfacial waves in a two-phase mixing layer.
Journal of Fluid Mechanics,
Vol. 921,
Issue. ,
Hu, Kai-Xin
Du, Kang
and
Chen, Qi-Sheng
2024.
Nonlinear waves in a sheared liquid film on a horizontal plane at small Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 999,
Issue. ,
Jain, Neha
and
Sharma, Gaurav
2025.
Effect of imposed shear stress on the stability of surfactant-laden liquid film flow over a rod.
European Journal of Mechanics - B/Fluids,
Vol. 111,
Issue. ,
p.
229.
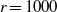 $r= 1000$, we find large regions of parameter space that produce absolute instability. These parameter regimes involve viscosity ratios of direct relevance to oil and gas flows. If, instead, the gas layer is laminar, absolute instability persists for the density ratio
$r= 1000$, we find large regions of parameter space that produce absolute instability. These parameter regimes involve viscosity ratios of direct relevance to oil and gas flows. If, instead, the gas layer is laminar, absolute instability persists for the density ratio  $r= 1000$, although the convective/absolute stability boundary occurs at a viscosity ratio that is an order of magnitude smaller than in the turbulent case. Two further unstable temporal modes exist in both the laminar and the turbulent cases, one of which can exclude absolute instability. We compare our results with an experimentally determined flow-regime map, and discuss the potential application of the present method to nonlinear analyses.
$r= 1000$, although the convective/absolute stability boundary occurs at a viscosity ratio that is an order of magnitude smaller than in the turbulent case. Two further unstable temporal modes exist in both the laminar and the turbulent cases, one of which can exclude absolute instability. We compare our results with an experimentally determined flow-regime map, and discuss the potential application of the present method to nonlinear analyses.

