Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T07:18:50.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Yield-Risk Measurements of the Performance of Common Stocks

Published online by Cambridge University Press:  19 October 2009

Robert M. Soldofsky  and
Roger Biderman
Get access Rights & Permissions [Opens in a new window]

Extract

Two general methods of computing the rate of return on common stock are being discussed widely. These methods are the internal rate of return and the geometric mean of the annual rates of return. The Gordon-Shapiro formulation, 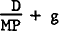, is the best known model of the former type.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 3 , Issue 1 , March 1968 , pp. 59 - 74
Copyright
Copyright © School of Business Administration, University of Washington 1968

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Another internal rate of return model is identified with Samuel Guild and Robert M. Soldofsky. These authors use formulations which discount both the expected dividend stream and the expected terminal market price to an equality with the initial market price. For a history of the internal rate of return models see Soldofsky, Robert M., “The History of Bond Tables and Stock Valuation Models,” Journal of Finance (03 1966) pp. 103–111.Google Scholar

2 Fisher, L. and Lorie, J. H., “Rates of Return on Investments in Common Stocks,” The Journal of Business (01 1964), pp. 1–21.Google Scholar

3 Herzog, John P., “Investor Experience in Corporate Securities: A New Technique for Measurement,” Journal of finance (03 1964), pp. 46–62.Google Scholar

4 Soldofsky, Robert M., “Growth Yields on Common Stock Since 1900,” Quarterly Review of Economics and Business (Winter 1965), pp. 51–61.Google Scholar

5 Hewitt, and Associates, , 1965 Report on the. Investment of Performance of Retirement Funds (Libertyville, Illinois: Hewitt Associates, 1966).Google Scholar

6 For a rigorous discussion of the differences between the internal rate of return and the geometric mean of the annual returns, see Ben-Shahar, Haim and Sarnat, Marshall, “Reinvestment and the Rate of Return on Common Stock,” Journal of Finance (12 1966), pp. 737–742.Google Scholar

7 Only part of the results are presented in the tables included in this article. The same measurements of performance were also prepared for the Moody's Bank Stocks and Insurance Stocks Series.

8 For a discussion of this model and the Gordon-Durand model see Soldofsky, Robert M., “The History of Bond Tables and Stock Valuation Models,” Journal of Finance (03 1966), pp. 103–111.Google Scholar

9 This method of computing the geometric mean is discussed and illustrated by Markowitz. Markowitz, Harry M., Portfolio Selection (New York: John Wiley and Sons, Inc., 1959), pp. 116–124.Google Scholar

10 Markowitz, Harry, “Portfolio Selection,” Journal of Finance (03 1952) p. 91.Google Scholar