Article contents
Using Investment Portfolios to Change Risk**
Published online by Cambridge University Press: 19 October 2009
Extract
It is well known that different combinations of investments involve different risks. In recent years the analysis of risk has tended to focus on two moments of the probability distribution of returns, the mean and variance. This paper considers the effect on the variance of an investment fund of adding dependent investments.
- Type
- Research Article
- Information
- Copyright
- Copyright © School of Business Administration, University of Washington 1968
References
1 See Markowitz, H. M., Portfolio Selection: Efficient Diversification of Investments (New York: John Wiley & Sons, 1959)Google Scholar and Sharpe, W. F., “Capital Asset Prices: A Theory of Market Equilibrium Under Conditions of Risk,” The Journal of Finance, 09 1964, pp. 425–442Google Scholar or Sharpe, W. F., “A Simplified Mold for Portfolio Analysis,” Management Science, 01 1963, pp. 277–293Google Scholar. A future paper will discuss the appropriateness of using means and variances.
2 See Samuelson, Paul A., “General Proof that Diversification Pays,” Journal of Financial and Quantitative Analysis, 03 1967, pp. 1–13Google Scholar, for a sophisticated discussion and proof of the usefulness of diversification.
3 It should be recalled that:
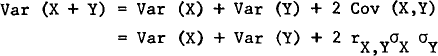 where rX, Y is the correlation coefficient of X, Y, and −1 ≤ rX, Y ≤ 1.
where rX, Y is the correlation coefficient of X, Y, and −1 ≤ rX, Y ≤ 1.
4 We are assuming Var(Y) ≥ Var(X) and identical means.
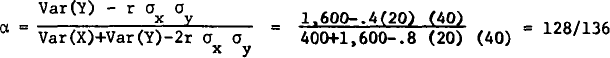
6 This conclusion was pointed out to the author by K. Larry Hastie when he was a graduate student at Cornell. See Hastie, K. Larry, “The Determination of Optimal Investment Policy,” Management Science, 08 1967, pp. 757–774. 156Google Scholar.
- 6
- Cited by


