Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-12-02T23:49:54.488Z Has data issue: false hasContentIssue false
  • English
  • Français

Systematic Interest-Rate Risk in a Two-Index Model of Returns

Published online by Cambridge University Press:  19 October 2009

Bernell K. Stone
Get access Rights & Permissions [Opens in a new window]

Extract

In the linear market-index model of the return-generating process, return on security j is given by

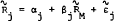
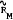where αj and βj are constants characteristic of company j, is return on a market index, and 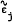is the company-specific component of return such that 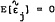and 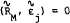. The coefficient βj is given by 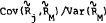. It is known as market responsiveness, volatility, systematic risk, and, more commonly, simply as “beta.” It has been widely accepted as a measure of nondiversifiable risk and incorporated in popular performance measures. Many stock information services now provide estimates of beta.

Type
Las Vegas Versus the Stock Market
Information
Journal of Financial and Quantitative Analysis , Volume 9 , Issue 5 , November 1974 , pp. 709 - 721
Copyright
Copyright © School of Business Administration, University of Washington 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bildersee, J.S. “Some Aspects of the Performance of Non-Convertible Preferred Stocks.” Journal of Finance, December 1973.Google Scholar
[2]Black, F., and Scholes, M.. “The Effect of Dividends on Common Stock Prices: A New Methodology.” Working Paper, August 1970; Revised August 1971.Google Scholar
[3]Black, F.; Jensen, M.C.; and Scholes, M.. “The Capital Asset Pricing Model: Some Empirical Tests.” In Studies in the Theory of Capital Markets, edited by Jensen, M.C.. New York: Praeger, 1972.Google Scholar
[4]Blume, M. “On the Assessment of Risk.” Journal of Finance, March 1971.CrossRefGoogle Scholar
[5]Blume, M. and Friend, I.. “A New Look at the Capital Asset Pricing Model.” Journal of Finance, March 1973.Google Scholar
[6]Brennen, M.J. Investor Taxes, Market Equilibrium, and Corporate Finance. Unpublished Ph.D. thesis, Massachusetts Institute of Technology, 1970.Google Scholar
[7]Cohen, K.J., and Pogue, G.A.. “An Empirical Evaluation of Alternative Portfolio Selection Models.” Journal of Business, April 1967.Google Scholar
[8]Fama, Eugene F., and MacBeth, James. “Risk, Return, and Equilibrium: Some Empirical Tests.” Journal of Political Economy, May–June, 1973.Google Scholar
[9]Friend, I., and Blume, M.. “Measurement of Portfolio Performance under Uncertainty.” American Economic Review, September 1970.Google Scholar
[10]Jacob, Nancy L. “The Measurement of Systematic Risk for Securities and Portfolios: Some Empirical Results.” Journal of Financial and Quantitative Analysis, March 1971.Google Scholar
[11]Jensen, M.C. “Risk, the Pricing of Capital Assets, and the Evaluation of Investment Portfolios.” Journal of Business, April 1969.Google Scholar
[12]Kraus, Alan, and Litzenberger, Robert H.. “Skewness Preference and the Valuation of Risk Assets.” Working Paper, December 1972.Google Scholar
[13]Levy, R.A. “Stationarity of Beta Coefficients.” Financial Analysts Journal, November–December 1971.CrossRefGoogle Scholar
[14]Lintner, John. “The Valuation of Risk Assets and the Selection of Risky Investments in Stock Portfolios and Capital Budgets.” Review of Economics and Statistics, February 1965.Google Scholar
[15]Roll, Richard. “Bias in Fitting the Sharpe Model to Time Series Data.” Journal of Financial and Quantitative Analysis, September 1969.Google Scholar
[16]Sharpe, W.F. “Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk.” Journal of Finance, September 1969.Google Scholar
[17]Sharpe, W.F.Portfolio Theory and Capital Markets. New York: McGraw Hill, 1970.Google Scholar
[18]Sharpe, W.F. “Bonds vs. Stocks: Capital Market Theory.” Financial Analysts Journal, November–December 1973.CrossRefGoogle Scholar
[19]Sharpe, W.F. “The Capital Asset Pricing Model: A Multi-Beta Interpretation.” Stanford University Research Paper No. 183, revised March 1974.Google Scholar