Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-24T04:35:21.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of Measurement Errors on Systematic Risk and Performance Measure of a Portfolio

Published online by Cambridge University Press:  06 April 2009

Cheng F. Lee  and
Frank C. Jen
Get access Rights & Permissions [Opens in a new window]

Extract

In this paper, we examine the effects of errors in measurement of the two independent variables, return on market (Rm) and return on risk-free assets (Rf), in the traditional one-factor capital asset pricing model (CAPM). After discussing Sharpe-Lintner's CAPM and both Jensen and Fama's specifications thereof, we review briefly the recent results of Friend and Blume [6], hereafter FB; Black, Jensen and Scholes [1], hereafter BJS; and Miller and Scholes (11], hereafter MS. In Section II, we first explore possible sources of measurement errors for both Rm and Rf; then we specify these errors mathematically and derive analytically their effects on estimates of systematic risk of a security or portfolio, 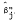, and the Jensen's measure of performance, 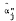. In Section III, we derive an analytical expression for the regression coefficient of estimated b's where we estimate the equation 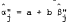. The result is then examined to find the conditions under which errors in measurement of Rm and Rf can cause b to have a positive or negative value even if the true b is zero. The conditions are then used to examine FB's results and their interpretation. In Section IV, an alternative hypothesis testing procedure for the CAPM is examined. We show that the empirical results so derived are also affected by the measurement errors and the sample variation of the systematic risk. The relative advantage between the two different testing hypothesis procedures is then explored. Finally, we comment on the relevance of the result to the popular zero-beta model and indicate areas for further research.

Type
Research Article
Information
Journal of Financial and Quantitative Analysis , Volume 13 , Issue 2 , June 1978 , pp. 299 - 312
Copyright
Copyright © School of Business Administration, University of Washington 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Black, F.; Jensen, M. C.; and Scholes, M.. “The Capital Asset Pricing Model: Some Empirical Tests.” In Studies in the Theory of Capital Markets, edited by Jensen, M. C.. New York: Praeger Publishers (1972).Google Scholar
[2]Blume, M., and Friend, I.. “A New Look at the Capital Asset Pricing Model.” Journal of Finance, Vol. 28 (1973), pp. 19–33.CrossRefGoogle Scholar
[3]Brennan, M. J. “Capital Market Equilibrium with Divergent Borrowing and Lending Rate.” Journal of Financial and Quantitative Analysis, Vol. 7 (1971), pp. 1197–1205.CrossRefGoogle Scholar
[4]Cramer, H.Mathematical Methods of Statistics. Princeton University Press (1946).Google Scholar
[5]Fama, E. F. “Risk, Return and Equilibrium: Some Clarifying Comments.” Journal of Finance, Vol. 23, No. 1 (1968), pp. 29–40.CrossRefGoogle Scholar
[6]Friend, I., and Blume, M.. “Measurement of Portfolio Performance under Uncertainty.” The American Economic Review, Vol. 60 (1970), pp. 561–75.Google Scholar
[7]Gailai, D., and Masulis, R. W.. “The Option Pricing Model and the Risk Factor of Stock.” Journal of Financial Economics, Vol. 3 (1976), pp. 53–81.CrossRefGoogle Scholar
[8]Jen, F. C. “Discussion on Random Walks and Technical Theories: Some Additional Evidence.” Journal of Finance, Vol. 25 (1970), pp. 495–499.Google Scholar
[9]Jensen, M. “The Performance of Mutual Funds in the Period 1954–1964.” Journal of Finance, Vol. 23 (1968), pp. 389–416.Google Scholar
[10]Johnston, J.Econometric Methods, 2nd ed.New York: McGraw-Hill (1972).Google Scholar
[11]Miller, M. H., and Scholes, M.. “Rates of Return in Relation to Risk: A Reexamination of Some Recent Findings.” In Studies in the Theory of Capital Market, edited by Jensen, M. C.. New York: Praeger Publishers (1972).Google Scholar
[12]Roll, R. “Bias in Fitting the Sharpe Model to Time Series Data.” Journal of Financial and Quantitative Analysis, Vol. 4 (1969), pp. 274–289.CrossRefGoogle Scholar
[13]Theil, H.Principles of Econometrics. New York: John Wiley and Sons, Inc. (1971).Google Scholar