No CrossRef data available.
Published online by Cambridge University Press: 19 October 2009
A well-known model of asset returns is the index equation
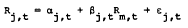
in which Rj, t is the observed rate of return on asset j during time period t; Rm, t is the return on a market index; βj, t is a parameter which measures the risk of asset j; αj, tis another parameter which has been given several interpretations by different authors; and εj, t is a stochastic disturbance term with zero mean. We discuss techniques for avoiding some of the pitfalls caused by nonstationarity. We explain a technique of robust regression; when the disturbances do not have all the standard spherical Gaussian properties so familiar from econometrics texts. We then describe a methodology for regression with a nonstationary model. It utilizes orthogonal polynomials of time to track the paths taken by the risk coefficient. This is a very robust specification and it has the potential to side-step many of the troubling theoretical and econometric problems of the model. By using the simple model we are not obliged to take sides on the question of which particular theory is “true” because this specification will be an approximation to all of the currently suggested theories (for a particular data sample). It is also reasonable to assert that the specification will approximate currently unknown models that may be developed in the future.