Introduction
The study of social networks has emerged as an interdisciplinary field spanning sociology, political science, economics, and computer science. Social networks provide services such as coordination (Opp and Gern, Reference Opp and Gern1993; Chwe, Reference Chwe2000), information (Duflo and Saez, Reference Duflo and Saez2003; Kremer and Miguel, Reference Kremer and Miguel2007; Conley and Udry, 2010) and trust (Karlan et al., Reference Karlan, Mobius, Rosenblat and Szeidl2009; Ambrus et al., Reference Ambrus, Mobius and Szeidl2014).
A key insight from the theory literature on networks is that network structure matters. For example, Granovetter (Reference Granovetter1974)’s classic study on job search identified “the strength of weak ties” for social learning. It is therefore important to measure social networks correctly in order to evaluate the suitability of a particular instance of a network for services such as trust or social learning. While weak ties are important for learning, strong ties tend to form the backbone of trust networks (Karlan et al., Reference Karlan, Mobius, Rosenblat and Szeidl2009; Jackson et al., Reference Jackson, Rodriguez-Barraquer and Tan2012; Gee et al., Reference Gee, Jones, Fariss, Burke and Fowler2017; Patacchini and Rainone, Reference Patacchini and Rainone2017).
However, it is not easy to recover a network of informal acquaintances, even when asking directly to the subjects. A network may be too large for asking everyone, Footnote 1 people may have problems in recalling all their friends, Footnote 2 friendships are bilateral relations, and only one out of two persons in a dyad may consider it an actual friendship. Footnote 3 Empirical researchers have used a wide variety of methods for eliciting network data.
To solve for the recalling and for the nonreciprocating problems mentioned above, one basic design question revolves around incentives: reporting one’s friends can be cumbersome and study participants might naturally tend to underreport friendships. This might be less of a concern with face-to-face surveys but becomes more salient when the elicitation is conducted over the phone or online. For this reason, incentivized network elicitation mechanisms have been developed starting with Leider et al. (Reference Leider, Mobius, Rosenblat and Do2009). Footnote 4 Typically, the researchers ask participants to list a certain number of friends (typically anywhere between 3 and 10) as well as certain attributes of the friendship (such as time spent together per week, for example). If a link is reciprocated, both participants get a small stochastic payoff which increases the more the reported attributes of a friendship align between the two reports. However, most incentivized protocols only elicit a truncated friends’ list with a uniform limit on the maximum number of elicited links. Footnote 5 Given the importance of network structure for network phenomena such as information diffusion and trust, this raises the question to what extent truncation matters.
A recent literature analyzes the importance of network mismeasurement on various estimation methods and contexts (Chandrasekhar and Lewis, Reference Chandrasekhar and Lewis2016; Breza et al., Reference Breza, Chandrasekhar, McCormick and Pan2020; Lee et al., Reference Lee, Liu, Patacchini and Zenou2021; Battaglini et al., Reference Battaglini, Patacchini and Rainone2022). The effects of censoring in peer effects estimates are studied in detail in Griffith and Peng (Reference Griffith and Peng2023). Little is known however on structural differences between truncated and complete (in the sense of completely elicited) networks and when those differences are most likely to matter.
In this paper, we provide insights into this debate using an experiment with high school students. We measure both complete networks (asking about links to every student in a class) and truncated networks (asking about up to five links in a class) and complement this information with supplemental questions on the amount of time each subject spends with each of the other students in the school. Our analysis reveals that the network mismeasurement in our population is largest for weak links. While 90% of weak links with friends spending 0–5 h per week together are underreported with truncated network elicitation, only 29% of strong links with subjects spending 16–20 h a week together are omitted. We thus expect larger biases in estimating network effects in context where weak ties may be more important than strong ties. We test this hypothesis through simulations where we show that the truncation of weak links reduces the number of “shortcuts” in the graph compared to the complete network which reduces the rate of social learning. In contrast, a randomly truncated network with the same degree distribution as the truncated graph but where we remove strong and weak links with the same probability behaves more like the complete network for information diffusion.
This finding suggests that additional resources in eliciting fuller network data have the highest returns when studying network services such as social learning which tend to operate along weak links. In contrast, studies of network services such as trust might be less affected because they are often thought to operate along stronger friendship links.
This paper is organized as follows. In the “Model” section, we review conditions under which our incentivized network elicitation induces truth-telling for both complete and truncated networks. We describe our experimental design in the “Experimental design” section. In the “Results” section, we discuss the results and run a simulation study to help understanding the consequences of truncation in terms of network topology. The “Discussion” section discusses modifications to incentivized network elicitation protocols that can reduce censoring measurement errors.
Model
We consider an undirected social network among a group of N agents. Each agent i has a link to every other agent j in the network and we denote the strength of the relationship between i and j with
![]() ${t_{ij}} \ge 0$
. In some studies, the intensity of relationship is simply measured by time spent together (such as Leider et al. (Reference Leider, Mobius, Rosenblat and Do2009)). In our study, we directly asked subjects for both the quality of their relationship and time spent together. We code the absence of a relationship with
${t_{ij}} \ge 0$
. In some studies, the intensity of relationship is simply measured by time spent together (such as Leider et al. (Reference Leider, Mobius, Rosenblat and Do2009)). In our study, we directly asked subjects for both the quality of their relationship and time spent together. We code the absence of a relationship with
![]() ${t_{ij}} = 0$
. We assume that both i and j know the strength of their relationship.
${t_{ij}} = 0$
. We assume that both i and j know the strength of their relationship.
Network elicitation. A researcher elicits M social network links for every agent. We say that elicitation is complete if
![]() $M = N- 1$
. Otherwise, we say elicitation is censored. The researcher asks every agent to list M links as well as the link intensity. We denote the agent’s choice of links with
$M = N- 1$
. Otherwise, we say elicitation is censored. The researcher asks every agent to list M links as well as the link intensity. We denote the agent’s choice of links with
![]() ${R_i}$
and the reported link intensity for every
${R_i}$
and the reported link intensity for every
![]() $j \in {R_i}$
with
$j \in {R_i}$
with
![]() ${\hat t_{ij}}$
: note that the report does not have to equal the true strength. For each agent, one of her reported links is chosen at random and her responses are compared to the responses of the other player. If two agents list each other and their reports coincide, then both of them are eligible for a lottery prize L. If the reports do not coincide or the other person does not list them, then the payoff is
${\hat t_{ij}}$
: note that the report does not have to equal the true strength. For each agent, one of her reported links is chosen at random and her responses are compared to the responses of the other player. If two agents list each other and their reports coincide, then both of them are eligible for a lottery prize L. If the reports do not coincide or the other person does not list them, then the payoff is
![]() $0$
.
$0$
.
To summarize, in this elicitation game an agent’s action can be summarized by
![]() $\left( {{M_i},\left( {{{\hat t}_{ij}}} \right)} \right)$
. We say an equilibrium is truthful if all the reports are truthful.
$\left( {{M_i},\left( {{{\hat t}_{ij}}} \right)} \right)$
. We say an equilibrium is truthful if all the reports are truthful.
Proposition 1 Under complete network elicitation truth-telling is an equilibrium.
Proof: Since network elicitation is complete, there is no strategic choice in whom to list. If other players tell the truth, then the best response is to be truthful, too.
Under censored network elicitation agents have a strategic choice in whom to list. In this case, we have to be careful about what agents know about their friends’ friends.
Assumption 1
Agents cannot observe the link intensity of network links that they are not a part of. They assume that each unobserved link is drawn i.i.d. from some distribution
![]() $F\left( t \right)$
over
$F\left( t \right)$
over
![]() $\left[ {0,\infty } \right]$
.
$\left[ {0,\infty } \right]$
.
We call this the “limited knowledge” assumption.
With limited knowledge and censored elicitation, we can show that there exist truthful and monotonic equilibria where agents list their strongest links when asked.
Proposition 2 Assume limited knowledge and censored network elicitation. Consider the strategy profile where all agents report their M strongest links truthfully. This is a Bayesian Nash equilibrium.
Proof: Truth-telling is immediate: conditionally on being listed by the other agent it is a best response to tell the truth if the other agent does so. Now assume that the agent would swap out a stronger link j for a weaker ink
![]() $j{\rm{'}}$
. She knows that the probability that she is among the M strongest links of j is larger than the probability that she is among the M strongest links of
$j{\rm{'}}$
. She knows that the probability that she is among the M strongest links of j is larger than the probability that she is among the M strongest links of
![]() $j{\rm{'}}$
. Hence, the probability of having a reciprocated link report is strictly larger if she reports j instead of
$j{\rm{'}}$
. Hence, the probability of having a reciprocated link report is strictly larger if she reports j instead of
![]() $j{\rm{'}}$
. This shows that there is no profitable deviation by i.
$j{\rm{'}}$
. This shows that there is no profitable deviation by i.
Without limited knowledge, there are situations where an agent might not report her M strongest links. For example, if she knows that these friends are very popular and have much stronger links, then she might not want to list them because it is unlikely that they will reciprocate.
Monotonic equilibria are intuitive equilibria of this game because we expect that even completely non-strategic agents will behave similarly. Models of human memory from behavioral psychology, for example, predict that agents are more likely to retrieve links with high intensity from their memory. These models of “what comes to mind” are reviewed by Kahana (Reference Kahana2012).
Experimental design
The experiment took place in April 2016 at a technical high school focusing on Science Technology, Engineering, and Mathematical Sciences. Students from across the region attend the school and select a concentration from majors such as informatics, life sciences, or chemistry. They spend most of their school career with the same group of 15–20 students. About 13% of students have an immigrant background indicated by a non-Italian last name. Only 23.4% of the students are female.
We used the lottery method to elicit complete networks from 554 students in 30 classrooms. We presented subjects with a complete list of students in their group and asked them to classify each potential link along two dimensions. First of all, we asked them to qualitatively describe their link to another student in the group as a “strong friendship,” “weak friendship,” or an “acquaintance.” We additionally asked a second question namely the amount of time the subject spent with that other student per week outside the classroom (with an ordinal scale of time spent with 1 = 0–5 h, 2 = 6–10 h, 3 = 11–15 h, 4 = 16–20 h, and 5 = more than 20 h). We considered the corresponding responses of two participants to be in agreement if they agree on both dimensions. In that case, both participants would receive a lottery ticket that would pay a monetary prize with some probability. This probability was fixed and did not depend on the number of total tickets assigned to students. A student could collect anywhere from
![]() $0$
tickets (if their answers were always in disagreement) to a ticket count equal to the number of students in their classroom (if they always agreed). Participants only learned the final sum of realized payoffs but not the number of tickets that they earned. This was to ensure that participants would not be able to directly infer the number of reciprocated links and to avoid disappointment on the part of participants.
$0$
tickets (if their answers were always in disagreement) to a ticket count equal to the number of students in their classroom (if they always agreed). Participants only learned the final sum of realized payoffs but not the number of tickets that they earned. This was to ensure that participants would not be able to directly infer the number of reciprocated links and to avoid disappointment on the part of participants.
For 216 students in another random set of classrooms in the same school, we conducted a censored network survey in which we asked subjects to list five or fewer friends. Footnote 6 The incentives were otherwise the same as for the full network elicitation game. Due to the random assignment of classrooms to complete and truncated network elicitation, we can therefore compare means of network statistics to understand the causal impact of censoring.
Results
We start by comparing the types of links that are elicited using the complete and truncated elicitation protocol. We verify that truncation tends to omit weaker links where friends spend less time with each other.
We then show that truncation not only elicits a sparser network compared to complete network elicitation but also changes the structure of the social network on top of this by making the network more clustered. This reduces diffusion which we show through simulating a simple SI model.
Link-level comparisons of complete and truncated networks
For the complete network, we elicited
![]() $1,777$
(
$1,777$
(
![]() $13.46{\rm{\% }}$
) strong friendships,
$13.46{\rm{\% }}$
) strong friendships,
![]() $7,729$
(
$7,729$
(
![]() $58.56{\rm{\% }}$
) weak friendships, and
$58.56{\rm{\% }}$
) weak friendships, and
![]() $3,692$
(
$3,692$
(
![]() $27.97{\rm{\% }}$
) acquaintances. For the truncated network, we elicited
$27.97{\rm{\% }}$
) acquaintances. For the truncated network, we elicited
![]() $366$
(
$366$
(
![]() $51.19{\rm{\% }}$
) strong friendships,
$51.19{\rm{\% }}$
) strong friendships,
![]() $277$
(
$277$
(
![]() $38.74{\rm{\% }}$
) weak friendships, and
$38.74{\rm{\% }}$
) weak friendships, and
![]() $72$
(
$72$
(
![]() $10.07{\rm{\% }}$
) acquaintances. Table 1 presents the amount of time subjects reported spending with each of their elicited links.
$10.07{\rm{\% }}$
) acquaintances. Table 1 presents the amount of time subjects reported spending with each of their elicited links.
Table 1. Breakdown of time spent, by friendship and network type

Table 2 shows that in the truncated network, the proportion of close friends listed is nearly four times as great as it is in the complete network. The majority of links in the complete network (
![]() $58.56$
%) are weak friends while the majority of links in the truncated network are strong friends (
$58.56$
%) are weak friends while the majority of links in the truncated network are strong friends (
![]() $51.19$
%).
$51.19$
%).
Table 2. Percentage of friendship type, by network type

Table 3 illustrates the same insight when aggregating along time spent together (rather the quality of the friendship). For the truncated network, the distribution is shifted toward links with whom the respondent spends more time. Table 4 shows the mean value of the ordinal time variable, by link type, across the two treatments: conditional on reporting a strong link there is no significant difference in the amount of time spent together between the complete and truncated network. When reporting a weak link or an acquaintance, respondents in the truncated networks report links with whom they spend significantly more time together but the difference is economically small (less than 20%). Truncation induces underreporting of weak links overall rather than underreporting of “weakest-weak” links.
Table 3. Percentage of time spent with friends, by network type

Table 4. Average time with friend, by friendship and network type

Notes. Standard errors in parentheses.
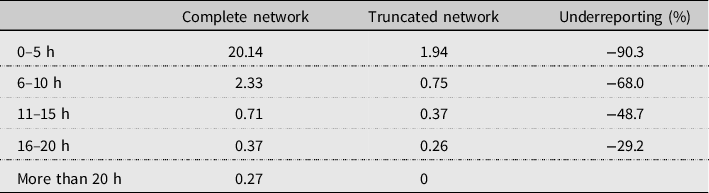
Table 5 summarizes the extent of the underreporting of links in the truncated protocol. In this table, we calculate the average number of links by time category and respondent. 90.3% of links in the 0–5 h per week category are missing compared to the complete network elicitation protocol while for links in the 16–20 h per week category only 29.2% of links are missing. Table 5 confirms that the largest measurement errors occur with weak links.
Table 5. Extent of underreported links per agent
Simulating diffusion on truncated networks
In this section, we design a simulation experiment to provide further insights on the implications of truncation for diffusion processes, that area phenomena commonly studied on social networks (in particular for models of social learning). The truncated network is of course more sparse than the complete network; therefore, mechanically, diffusion will be faster on the complete network compared to the truncated network. In order to identify the marginal impact of truncated network elicitation on top of sparsity, we create “randomly truncated” networks where we randomly select, for each agent, five links from the completely elicited network. We draw 1,000 such randomly truncated networks to minimize simulation error.
Table 6 reports network topology measures for the complete, truncated, and randomly truncated networks without symmetrizing the networks while Table 7 shows statistics for symmetrized OR-networks (a link exists if either respondent names the other). Statistics such as diameter and clustering coefficient are commonly defined on the symmetrized networks only.
Table 6. Comparison of network statistics for complete, truncated, and randomly truncated networks (directed network)

Note: Sample standard errors in parentheses. The complete network consists of 30 classrooms and the truncated network was elicited in 15 classrooms. The randomly truncated network was drawn 1,000 from complete elicitations (5 links per respondent). The random addition network does the reverse exercise and adds random friends to each truncated network to make it degree-comparable to the complete network. Degree is calculated on the directed network. The SI simulations pick a node at random as seed, infects outlinks with probability
![]() ${1 \over 2}$
, and continues for 3 steps. The percentage of infected nodes is reported.
${1 \over 2}$
, and continues for 3 steps. The percentage of infected nodes is reported.
Table 7. Comparison of network statistics for complete, truncated, and randomly truncated networks (symmetrized OR-network)

Note: Sample standard errors in parentheses. The complete network consists of 30 classrooms and the truncated network was elicited in 15 classrooms. The randomly truncated network was drawn 1,000 from complete elicitations (5 links per respondent). The random addition network does the reverse exercise and adds random friends to each truncated network to make it degree-comparable to the complete network. Degree is calculated on the symmetrized network.
The most striking difference between the truncated and randomly truncated networks is that the truncated networks are far more clustered (0.25 versus 0.07): this is intuitive because truncation preserves strong links which tend to be more clustered than weak links. Therefore, the truncated network also has a larger diameter compared to the randomly truncated network (4.13 versus 3.23).
Because higher clustering and higher diameter reduce the speed of diffusion in truncated networks, we expect an important cost of truncation in terms of signal transmission over the network. To demonstrate this, we simulate an SI model which is one of the simplest models of infectious diseases and which can also be interpreted as a simple model of information diffusion. Time is discrete and a random node is picked at time
![]() $t = 0$
. Outlinks are infected with probability
$t = 0$
. Outlinks are infected with probability
![]() ${1 \over 2}$
and we simulate diffusion for 3 time periods and then record the share of infected nodes. Results are shown in the last column of Table 6. It appears that in the truncated network only 67% of agents are infected while in the randomly truncated network the share is 75% and closer to the diffusion speed in the complete network. This exercise therefore helps understanding how truncation can make us underestimate the speed of diffusion in real-world social networks by omitting weak links.
${1 \over 2}$
and we simulate diffusion for 3 time periods and then record the share of infected nodes. Results are shown in the last column of Table 6. It appears that in the truncated network only 67% of agents are infected while in the randomly truncated network the share is 75% and closer to the diffusion speed in the complete network. This exercise therefore helps understanding how truncation can make us underestimate the speed of diffusion in real-world social networks by omitting weak links.
As an added exercise, we also “simulate” complete networks by starting with the truncated networks and randomly adding links to match the degree of the complete networks. The results are reported in the last rows of Tables 6 and 7. The diameter of these randomly increased networks is smaller than the true complete network because the randomly drawn links create more shortcuts in the graph. However, clustering as well as speed of diffusion is comparable to the complete network and within the error bounds. These results support the intuition that the truncated weaker links are largely random links in the networks.
Discussion
We have shown that truncation induces serious measurement errors that affect our understanding of the structure of a social network. Intuitively, these errors should be most serious for popular respondents who have many friends and for whom the truncation cutoff is therefore more likely to bind. Based on this intuition, we are looking for protocols that endogenize the truncation cutoff: we would like popular respondents to report more friends compared to less popular respondents.
This can be achieved by making agent i’s probability of receiving lottery prize L dependent on the number of her link submissions
![]() ${M_i}$
. More precisely, we consider mechanisms where the probability of receiving a ticket is an increasing and concave function
${M_i}$
. More precisely, we consider mechanisms where the probability of receiving a ticket is an increasing and concave function
![]() $p\left( {{M_i}} \right)$
.
$p\left( {{M_i}} \right)$
.
To state our next result, we introduce a notion of popularity: consider two agents i and j and their realized friendship intensities with all other
![]() $N - 1$
neighbors. Assume that we order – for each agent – her links from the strongest to the weakest. We say that agent i is more popular than agent j if for any
$N - 1$
neighbors. Assume that we order – for each agent – her links from the strongest to the weakest. We say that agent i is more popular than agent j if for any
![]() $1 \le M\le N- 1$
agent i’s Mth link has larger intensity than j’s Mth link.
$1 \le M\le N- 1$
agent i’s Mth link has larger intensity than j’s Mth link.
Proposition 3
Assume that the agent has a fixed cost c for reporting on a link, that agents have limited knowledge and that agent i decides on the number of links
![]() ${M_i}$
to submit. The agent is eligible for the lottery prize L with probability
${M_i}$
to submit. The agent is eligible for the lottery prize L with probability
![]() $P\left( {{M_i}} \right)$
where
$P\left( {{M_i}} \right)$
where
![]() $P\left( 0 \right) = 0$
and
$P\left( 0 \right) = 0$
and
![]() $P\left( \cdot \right)$
is a strictly increasing and concave function. There is a truthful Bayesian Nash equilibrium where agent i reports her
$P\left( \cdot \right)$
is a strictly increasing and concave function. There is a truthful Bayesian Nash equilibrium where agent i reports her
![]() ${M_i}$
strongest links truthfully. Moreover, in any such equilibrium more popular agents will report weakly more links.
${M_i}$
strongest links truthfully. Moreover, in any such equilibrium more popular agents will report weakly more links.
Proof: The marginal increase in the probability of receiving a link is equal to
![]() $p\left( M\right)/M$
which is decreasing with M. The probability that a link is reciprocated is also decreasing in the link intensity. An agent will only report link M if the marginal increase in the probability of getting lottery L times the probability of the link being reciprocated exceeds cost c. Therefore, if j reports her Mth link, then a more popular agent will certainly report it as well.
$p\left( M\right)/M$
which is decreasing with M. The probability that a link is reciprocated is also decreasing in the link intensity. An agent will only report link M if the marginal increase in the probability of getting lottery L times the probability of the link being reciprocated exceeds cost c. Therefore, if j reports her Mth link, then a more popular agent will certainly report it as well.
Note that our proposed mechanisms will generally not solve the measurement problem completely. However, it provides support for incentivized network elicitation with dynamic truncation.
Conclusion
We find in our population of high school students that when truncating the friendship list to five links we drastically undercount weak links but only moderately undercount strong links. The truncated network has a larger diameter and is more clustered than a randomly truncated network which impedes information diffusion.
An implication of this finding is that truncation error might have more impact when studying network services such as social learning which tend to operate along weak links. In contrast, studies of network services such as trust might be less affected because they are often thought to operate along stronger friendship links.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/XPS.2023.23
Data availability
The data, code, and any additional materials required to replicate all analyses in this paper are available at the Journal of Experimental Political Science Dataverse within the Harvard Dataverse Network, at: https://doi.org/10.7910/DVN/4XXIAG (Morton et al., Reference Morton, Patacchini, Pin, Rogers and Rosenblat2023).
Competing interests
The authors have no conflicts of interest.
Ethics statements
This study was approved by the NYU Abu Dhabi IRB (#043-2015). The research adheres to the APSA’s Principles and Guidance for human subjects research (https://connect.apsanet.org/hsr/principles-and-guidance/). Subjects could earn Amazon gift certificates in this experiment worth 5 Euros: by playing the experimental games well they increased their chances of earning a certificate.









