Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-28T06:52:30.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Introducing a sinusoidal equation to describe lactation curves for cumulative milk yield and composition in Holstein cows

Published online by Cambridge University Press:  07 May 2020

Navid Ghavi Hossein-Zadeh ,
Hassan Darmani Kuhi ,
James France  and
Secundino López
Navid Ghavi Hossein-Zadeh
Affiliation:
Department of Animal Science, Faculty of Agricultural Sciences, University of Guilan, Rasht, Iran
Hassan Darmani Kuhi*
Affiliation:
Department of Animal Science, Faculty of Agricultural Sciences, University of Guilan, Rasht, Iran
James France
Affiliation:
Department of Animal Biosciences, Centre for Nutrition Modelling, University of Guelph, GuelphON, N1G 2W1, Canada
Secundino López
Affiliation:
Instituto de Ganadería de Montaña (IGM), CSIC-Universidad de León, Departamento de Producción Animal, Universidad de León, E-24007León, Spain
*
Author for correspondence: Hassan Darmani Kuhi, Email: [email protected]; [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The aim of the work reported here was to investigate the appropriateness of a sinusoidal function by applying it to model the cumulative lactation curves for milk yield and composition in primiparous Holstein cows, and to compare it with three conventional growth models (linear, Richards and Morgan). Data used in this study were 911 144 test-day records for milk, fat and protein yields, which were recorded on 834 dairy herds from 2000 to 2011 by the Animal Breeding Centre and Promotion of Animal Products of Iran. Each function was fitted to the test-day production records using appropriate procedures in SAS (PROC REG for the linear model and PROC NLIN for the Richards, Morgan and sinusoidal equations) and the parameters were estimated. The models were tested for goodness of fit using adjusted coefficient of determination 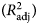$\lpar {R_{{\rm adj}}^2 } \rpar $, root mean square error (RMSE), Akaike's information criterion (AIC) and the Bayesian information criterion (BIC). 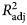$R_{{\rm adj}}^2 $ values were generally high (>0.999), implying suitable fits to the data, and showed little differences among the models for cumulative yields. The sinusoidal equation provided the lowest values of RMSE, AIC and BIC, and therefore the best fit to the lactation curve for cumulative milk, fat and protein yields. The linear model gave the poorest fit to the cumulative lactation curve for all production traits. The current results show that classical growth functions can be fitted accurately to cumulative lactation curves for production traits, but the new sinusoidal equation introduced herein, by providing best goodness of fit, can be considered a useful alternative to conventional models in dairy research.

Keywords

Cumulative milk yielddairy cowgrowth functionlactation curvesinusoidal equation
Type
Research Article
Information
Journal of Dairy Research , Volume 87 , Issue 2 , May 2020 , pp. 220 - 225
Copyright
Copyright © Hannah Dairy Research Foundation 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adediran, SA, Malau-Aduli, AEO, Roche, JR and Donaghy, DJ (2007) Using lactation curves as a tool for breeding, nutrition and health management decisions in pasture-based dairy systems. In Fulkerson, B (ed.) Current Topics in Dairy Production, Proceedings of the Dairy Research Foundation Symposium. vol. 12, Camden, New South Wales, Australia: The University of Sydney, pp. 74–78.Google Scholar
Ali, TE and Schaeffer, LR (1987) Accounting for covariances among test day milk yields in dairy cows. Canadian Journal of Animal Science 67, 637–644.CrossRefGoogle Scholar
Aziz, MA, Shalaby, NA, El-Shafie, OM, Mahdy, AT and Nishida, A (2006) Comparison between the shapes of lactation curve of Egyptian buffalo milk yield estimated by the incomplete gamma function and a new model. Livestock Research for Rural Developments 18, Article 59. Available at http://www.lrrd.org/lrrd18/5/aziz18059.htm.Google Scholar
Codrea, MC, Hojsgaard, S and Friggens, NC (2011) Differential smoothing of time-series measurements to identify disturbances in performance and quantify animal response characteristics: an example using milk yield profiles in dairy cows. Journal of Animal Science 89, 3089–3098.CrossRefGoogle ScholarPubMed
Darmani Kuhi, H, Ghavi Hossein-Zadeh, N, López, S, Falahi, S and France, J (2019 a) Sinusoidal function to describe the growth curve of dairy heifers. Animal Production Science 59, 1039–1047.CrossRefGoogle Scholar
Darmani Kuhi, H, López, S, France, J, Mohit, A, Shabanpour, A, Ghavi Hossein-Zadeh, N and Falahi, S (2019 b) A sinusoidal equation as an alternative to classical growth functions to describe growth profiles in turkeys. Acta Scientiarum. Animal Sciences 41, e45990.CrossRefGoogle Scholar
Dimauro, C, Cappio-Borlino, A, Macciotta, NPP and Pulina, G (2007) Use of a computer-aided design to develop a stress simulation model for lactating dairy sheep. Livestock Production Science 106, 200–209.CrossRefGoogle Scholar
Fahti Nasri, N, France, J, Odongo, NE, López, S, Bannink, A and Kebreab, E (2008) Modelling the lactation curve of dairy cows using the differentials of growth functions. Journal of Agricultural Science 146, 633–641.CrossRefGoogle Scholar
Ghavi Hossein-Zadeh, N (2014) Comparison of non-linear models to describe the lactation curves of milk yield and composition in Iranian Holsteins. Journal of Agricultural Science 152, 309–324.CrossRefGoogle Scholar
Ghavi Hossein-Zadeh, N (2017) Application of growth models to describe the lactation curves for test-day milk production in Holstein cows. Journal of Applied Animal Research 45, 145–151.CrossRefGoogle Scholar
López, S, France, J, Odongo, NE, McBride, RA, Kebreab, E, AlZahal, O, McBride, BW and Dijkstra, J (2015) On the analysis of Canadian Holstein dairy cow lactation curves using standard growth functions. Journal of Dairy Science 98, 2701–2712.CrossRefGoogle ScholarPubMed
Macciotta, NPP, Vicario, D and Cappio-Borlino, A (2005) Detection of different shapes of lactation curve for milk yield in dairy cattle by empirical mathematical models. Journal of Dairy Science 88, 1178–1191.CrossRefGoogle ScholarPubMed
Pulina, G and Nudda, A (2001) La produzione del latte. In Pulina, G (ed.), L'alimentazione degli ovini da latte. Bologna, Italy: Avenue Media, pp. 9–31.Google Scholar
Rekik, B and Ben Gara, A (2004) Factors affecting the occurrence of atypical lactations for Holstein-Friesian cows. Livestock Production Science 87, 245–250.CrossRefGoogle Scholar
SAS (2002) SAS User's Guide v. 9.1: Statistics. SAS Institute, Inc., Cary, NC.Google Scholar
Silvestre, AM, Petim-Batista, F and Colaço, J (2005) Genetic parameter estimates of Portuguese dairy cows for milk, fat and protein using a spline test-day model. Journal of Dairy Science 88, 1225–1230.CrossRefGoogle ScholarPubMed
Thornley, JHM and France, J (2007) Mathematical Models in Agriculture: Quantitative Methods for the Plant, Animal and Ecological Sciences, 2nd Edn.Wallingford, UK: CAB International.CrossRefGoogle Scholar
Wasike, CB, Kahi, AK and Peters, KJ (2011) Modelling of lactation curves of dairy cows based on monthly test day milk yield records under inconsistent milk recording scenarios. Animal: An International Journal of Animal Bioscience 5, 1780–1790.CrossRefGoogle ScholarPubMed
Supplementary material: PDF

Ghavi Hossein-Zadeh et al. supplementary material

Table S1 and Figures S1-S3

Download Ghavi Hossein-Zadeh et al. supplementary material(PDF)
PDF 416.1 KB