GENDER EQUALITY AND THE GENDER GAP IN MATHEMATICS

Summary

A gender gap has been found in mathematics (boys outperform girls) that has prevailed across countries for many decades. Whether this gap results from nature or nurture has been hotly debated. Using the evidence of PISA 2003 and the gender equality index of 2003, some researchers have argued that an improvement in gender equality reduces the gender gap in mathematics. This study used five waves of country-level PISA data and, controlling for country fixed effects, found no evidence to support this argument. Furthermore, individual data for PISA 2012 and the multilevel data model were used. The conclusion drawn also does not support the argument. In fact, the relationship between gender equality and the gender gap in mathematics vanished after PISA 2003.

Introduction

Ever since Benbow and Stanley (1980, 1983) published their findings on the gender gap in mathematics in the journal Science, the debate on the gender gap in mathematics has not ceased in recent decades (for example, see the discussions in Gallagher & Kaufman, 2005; Ceci & Williams, 2007, 2011; Ceci et al., 2009). New findings regarding the gender gap in mathematics have continuously emerged. While some might argue that the gap has been narrowed in some countries, it does not seem to have disappeared completely. Some researchers have argued that boys outperforming girls in mathematics is the consequence of a socialization process in which women are stratified into occupations so that they are bound to perform certain social roles requiring fewer mathematics skills (Baker & Jones, 1993). In other words, these researchers have argued that the gender gap in mathematics will decline as gender equality prevails (Guiso et al., 2008; Hyde & Mertz, 2009; Else-Quest et al., 2010; Kane & Mertz, 2012).

Accordingly, Guiso et al. (2008) and Else-Quest et al. (2010) applied the Programme for International Student Assessment (PISA) 2003 and found a negative correlation between gender equality and the gender gap in mathematics. They consequently concluded that the gender gap in mathematics results from socialization. Stoet and Geary (2013) employed four waves of the PISA and concluded that the gap is not associated with gender equality. Stoet and Geary (2015) further indicated that not only can the relation between the gender gap in mathematics and gender equality in 2003 not be replicated in PISAs of the other years, but also that the negative correlation found in PISA 2003 mainly results from outliers, i.e. the Nordic countries. They showed that the significant correlation between the gender gap in mathematics and gender equality in 2003 vanished when the Nordic countries were ruled out.

In recent decades, gender equality, though not completely prevalent worldwide, has been significantly improved in most countries, but the gender gap in mathematics has not correspondingly improved (Wai et al., 2010; see also Table 1). For example, the Gender Inequality Index (GII) is an index measuring gender disparity in a country. This was introduced in the 2010 Human Development Report published by the United Nations Development Programme to remedy the shortcomings of the previous indexes, namely the Gender Development Index (GDI) and the Gender Empowerment Measure (GEM). According to the GII in 2012, the Netherlands is the best country in terms of gender equality and Switzerland is the third best. Boys in the Netherlands and Switzerland still outperformed girls in PISA 2012 by scores of 10 and 13, respectively. The gender gaps in mathematics in these two countries are statistically significant. At the other pole of gender equality, Jordan and Qatar were ranked 99 and 117 in the 2012 GII, respectively. However, girls in Jordan and Qatar significantly outperformed their male counterparts by scores of 21 and 16, respectively. In PISA 2012, girls outperformed boys the most in these two Arabian countries among all of the participant countries. Fryer and Levitt (2010) speculated that this could be a consequence of single-sex school, which enhance girls’ learning. But Jackson (2012) postulated that same-sex education does not actually enhance girls’ academic performance.

Table 1 Gender gap in mathematics from the PISA and gender equality indicators

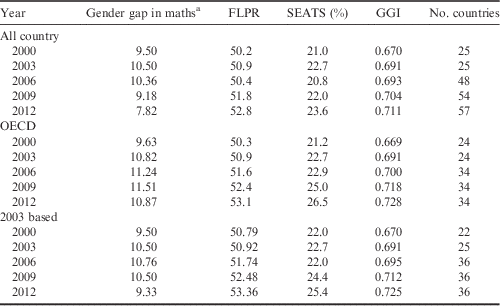
^a The gender gap is the boys’ minus girls’ average scores.

Data sources: The female labour participation rate (FLPR) and seats held by women in national parliaments (SEATS) were obtained from World Development Indicators compiled by the World Bank. The GGI (Gender Gap Index) was obtained from the Global Gender Gap Report published by the World Economic Forum.

The relations between GII (gender equality) and the gender gap in mathematics on the two opposite extremes of the spectrum of the gender equality scale contradict the hypothesis that gender equality is positively correlated with girls’ mathematics performance. By contrast, in addition to the socialization process, scientists have suggested that males and females have different brains (Baron-Cohen, 2003; Kimura, 2007; Halpern, 2012). As a result, gender equality is not necessarily correlated with the gender gap in mathematics.

This study used all five waves of the PISA data and more comprehensive models to re-examine this issue. The PISA 2003 was used as the benchmark to investigate whether previous findings on gender equality and the gender gap in mathematics could be replicated in other waves of the PISA data. The conclusion that gender equality can reduce the gender gap in mathematics from PISA 2003 encounters at least one challenge; that is, the correlation generated between countries cannot ensure the prevalence of the same correlation within a country. It is more reliable to confirm a correlation within a country by using longitudinal data or panel data.

Accordingly, PISA 2000, 2003, 2006, 2009 and 2012 country aggregate data and panel data models were used to investigate the relation between gender equality and the gender gap in mathematics. The results of the panel data models were compared with the results of the OLS analysis to see if the relations generated within a country were consistent with the relations generated between countries. More attention is paid to the sampled countries in PISA 2003 used by preceding studies, which argued the negative correlation between gender equality and the gender gap in mathematics. Stoet and Geary (2015) demonstrated that this correlation disappeared when outliers – the Nordic countries – were ruled out. Finally, because correlation generated from aggregate data might not exist in individual data, a three-level multilevel model was used to analyse individual data to verify if the relation found in aggregate data could also be found in individual data.

Data sources and the Gender Gap Index

The PISA has been conducted by the OECD every three years since 2000, and has been designed to assess the capability of 15-year-old students by their reading skills, mathematical skills and scientific knowledge. In addition to the OECD countries, some non-OECD countries have also participated in the PISA. The PISA published the results of 42, 39, 55, 65 and 65 countries for PISA 2000, PISA 2003, PISA 2006, PISA 2009 and PISA 2012, respectively. Note that the PISA may have published fewer results in terms of the number of countries than those of participant countries due to data quality.

The PISA does not publish students’ original scores, but instead publishes five plausible values (PVs) for each student. Conceptually, this does not represent a student’s true mathematics ability, in the same way as any parameter of a population is unobservable. In addition, true mathematics ability is continuous, whereas this score is an integer. The PISA constructs a posterior distribution for each student (see the PISA data analysis manual SAS, second edition, 2009, p. 97, or the PISA 2009 technical report, p. 139). The five PVs are then randomly drawn from each student’s posterior distribution. The process of generating the PVs standardizes its average to 500 and its standard deviation to 100 based on all OECD countries. It is therefore inappropriate to use a single country’s PISA time series data to justify whether students in that country have progressed in their mathematics tests. However, comparisons between the sexes within a country or among countries are appropriate since the criterion for each PISA wave is controlled. In other words, the PISA scores do not have absolute meaning but do have relative meaning.

This study used the recently developed Gender Equality Index or Gender Gap Index (GGI), published by the World Economic Forum, to represent the extent of a nation’s gender equality. Several alternatives to the GGI are available. For example, the GDI (Gross Domestic Income) and GEM (Gender Empowerment Measure), published by the United Nations Development Program (UNDP), have been available since 1995. However, GDI and GEM have been widely criticized for their usage, conceptual and methodological limitations (Bardhan & Klasen, 1999; Dijkstra & Hanmer, 2000; Dijkstra, 2002, 2006; Klasen, 2006; Schüler, 2006; Permanyer, 2013a). To respond to these criticisms, the UNDP proposed a new Gender Inequality Index (GII) in 2010. The GII was constructed to reflect a women’s disadvantage in three dimensions: empowerment, economic activity and reproductive health. The GII’s value lies between 0 and 1 and is meant to measure the loss in human development due to gender inequality (Gaye et al., 2010). A small GII denotes a small loss due to gender inequality, and hence is associated with a more gender-equal country. Permanyer (2013b) criticized the GII formula for being extremely complicated and difficult to interpret. Moreover, he argued that the GII formula inappropriately combines relative and absolute measures, and wrongfully penalizes gender-equal countries with low GDP. Furthermore, Permanyer (2013b) pointed out that even when women and men are perfectly equal in all dimensions, GII is substantially greater than zero.

The GGI has been published by the World Economic Forum in the Global Gender Gap Report since 2006, and the GGIs of many nations have been computed as early as the year 2000. The GGI has three underlying concepts and four pillars. The three underlying concepts are gaps, outcomes and gender equality. It measures gender-based gaps in terms of access to resources and opportunities rather than absolute levels of resources and opportunities available to both sexes. It is independent of a nation’s development level and ranks nations according to their output variables rather than the input measures through which governments strive to eliminate the gender gap. For example, the ratio of the female to male labour participation rate (output variable) is used to construct both GGI and GDI, while maternity leave benefits (the input to improve gender equality) is not used in GGI but is used in GDI. The GGI evaluates nations based on their proximity to gender equality rather than females’ empowerment. For example, the scaled value for a country’s ratio of females in secondary school is 1, the highest value, as long as equality is reached, regardless of how great the number of girls for every boy is.

The four pillars are economic participation and opportunity, educational attainment, health and survival, and political empowerment. Fourteen variables are chosen to represent these four pillars, and all these variables are converted to ratios of females to males. The equality benchmark of these ratios is considered to be 1, except for two health variables. The equality benchmarks for the sex ratio at birth and healthy life expectancy are adjusted for biological differences in the sexes, and are set to be 0.944 and 1.06, respectively. The normal sex ratio at birth of males to females is about 1.06. Its invert ratio is 0.944. The UN’s Gender-Related Development Index uses 87.5 years as the maximum age for females and 82.5 years as the maximum age for males, and the ratio of females’ to males’ maximum ages is 1.06. All these ratios are one-sided scales measuring how closely women reach parity with men. The methodology penalizes the ratios less than 1 but does not reward or penalize the ratios greater than 1. This procedure is to avoid over-compensation between different variables when women are on a par with men in certain variables.

Then, within each pillar sub-index, the weighted average is calculated, and the weights normalize their corresponding variables to have equal standard deviations. Since all variables are measured by ratios, the weighted average of each sub-index must lie between 0 and 1.

Finally, the final score of GGI is obtained from averaging the weighted averages of the four sub-indexes. It is important to note that an index would lose its comparability over time if its weighting values were to vary annually. To maintain its comparability over time, the computation of any year’s GGI uses the weight for the year 2006.

A score for GGI can be roughly interpreted as a percentage value revealing the degree to which women have reached parity with men. A GGI score of 0.85 for a country approximately means a 15% gender gap in that country. Many gender equality indexes are available (see the review in Bericat, 2012). The GGI was chosen not because it is superior to other gender equality indexes, but because GGI is available for all waves of the PISA, and is not as widely criticized as GDI or GEM. The other international gender equality index is the Gender Equity Index (GEI) published by Social Watch. The GEI is only available for 2004, 2007 to 2009 and 2012, and the GII is only available after 2010. Aside from the gender equality index, direct indicators of women’s economic and political activities are also used. They are the female labour participation rate (FLPR), and the proportion of seats held by females in parliament (SEAT).

Previous studies (Guiso et al., 2008; Else-Quest et al., 2010) used the data of PISA 2003 and found a negative relationship between gender equality and the gender difference in mathematics. In the present study the PISA 2003 participant countries were used as the benchmark to construct three country samples to explore the relationship between gender equality and the gender gap in mathematics. The first sample refers to the all-country sample, which includes all countries available. The second sample includes only the OECD countries, since the PISA starts with the OECD members. The third sample consists of the PISA 2003 participant countries. Defining these three country samples allows examination of whether the relationship between gender equality and the gender gap in mathematics found in PISA 2003 has persisted in these specific countries or has even been extended to the all-country sample.

Table 1 presents the gender differences in mathematics for all PISA waves and the gender equality indicators for the same year. It includes three samples: all country, OECD and 2003-based country samples. All figures in Table 1 were computed for those countries with available data. Table 1 shows that the gender gap in mathematics in the OECD sample is greater than that in the other two samples. This might result from more variable gender differences in mathematics for samples including non-OECD countries. Taking PISA 2012 as an example, the greatest gender gap in mathematics is 25 (Colombia), while the smallest one is −21 (Jordan). As for the OECD sample in the same year, although the greatest is still 25 (Chile and Luxembourg), the smallest is only −6 (Iceland). Table 1 does not exhibit a negative linear relationship between the gender gap in mathematics and the gender equality indicators. On average, the figures in Table 1 do not demonstrate that gender equality eliminates the gender gap in mathematics. Figure 1 depicts the relationship between the Gender Gap Index (GGI) and gender gap in mathematics (boys’−girls’ average scores). Indeed, as the literature has shown, the country-level data based on PISA 2000 and PISA 2003 reveal a negative relationship between GGI and the gender gap, but this relationship disappears after PISA 2003.

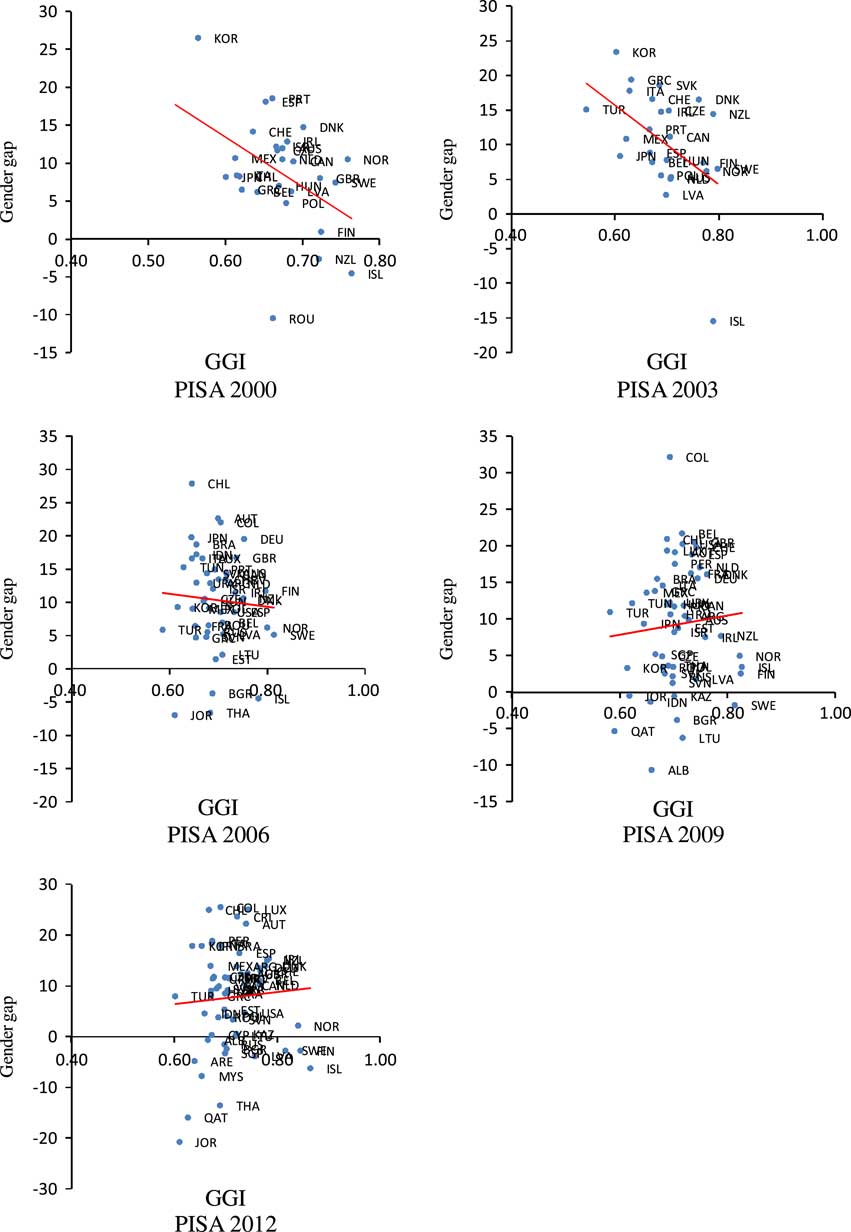
Fig. 1 Scatter plots of GGI vs gender difference in mathematics (PISA 2000 to PISA 2012).

Empirical models

Country-level data

To further explore the relationship between gender equality and the gender gap in mathematics, in addition to the three country samples, tests on all-wave data and single-wave data were conducted. Five waves of the PISA data were analysed by OLS (ordinary least squares) models clustered by country and analysed by panel data models. The OLS models do not control a country’s heterogeneity and their results cannot be used to draw conclusions for a given country. The results of the panel data models can, however, lead to conclusions for a given country. The results of these two types of models were compared. Second, to investigate whether the relationship between gender equality and the gender gap in mathematics found in PISA 2003 can also be found in other waves of the PISA, regressions were conducted wave by wave. Regression results from the all-wave and single-wave data for these three samples are presented.

The dependent variable in these models is the gender difference in mathematics (GD, boys’−girls’ average scores), and their explanatory variables include GGI, the female labour participation rate (FLPR), the proportion of seats held by women in parliament (SEAT) and GDP per capita measured in PPP (Purchasing Power Parity). The OLS and the panel data models are shown below. Equation (1) is the OLS model, whereas eqns (2) and (3) are, respectively, the fixed-effects panel data model (FEM) and the random-effects panel data model (REM); ε is the error term, β is the regression coefficient, α _k is the fixed individual effect for country k in the FEM, and v _k is the random individual effect for country k in the REM.

(1) $${\rm GD}_{{kt}} \,{\equals}\,\beta _{0} {\plus}\beta _{1} {\rm GGI}_{{kt}} {\plus}\beta _{2} {\rm FLPR}_{{kt}} {\plus}\beta _{3} {\rm SEAT}_{{kt}} {\plus}\beta _{4} {\rm GDP}_{{kt}} {\plus}{\epsilon}_{{kt}} $$

(2) $${\rm GD}_{{kt}} \,{\equals}\,\alpha _{k} {\plus}\beta _{1} {\rm GGI}_{{kt}} {\plus}\beta _{2} {\rm FLPR}_{{kt}} {\plus}\beta _{3} {\rm SEAT}_{{kt}} {\plus}\beta _{4} {\rm GDP}_{{kt}} {\plus}{\epsilon}_{{kt}} $$

(3) $${\rm GD}_{{kt}} \,{\equals}\,\beta _{1} {\rm GGI}_{{kt}} {\plus}\beta _{2} {\rm FLPR}_{{kt}} {\plus}\beta _{3} {\rm SEAT}_{{kt}} {\plus}\beta _{4} {\rm GDP}_{{kt}} {\plus}v_{k} {\plus}{\epsilon}_{{kt}} $$

The GGI is a composite index of gender equality, which must be correlated with the other explanatory variables in the equations above, in particular FLPR and SEAT. Following Else-Quest et al. (2010), each of these equality indexes (GGI, FLPR, SEAT) was included in the model one at a time. Similarly, the one-variable OLS and panel data models 1, 2 and 3 were applied to the all-country sample, the OECD sample and the 2003-based sample, respectively.

Individual-level data

The PISA warns that plausible values should not be used to represent individual performance. These five PVs should not be averaged at the student level to estimate the students’ average performance since, even though this average is an unbiased estimator of the students’ performance, doing so will bias its variance estimator. The PISA uses a two-stage sampling design to draw student samples. Schools are first sampled, and students in those schools are then sampled. This sampling design is more complicated than the simple random sampling design. The PISA’s sampling design not only increases the variance of an estimator, but also makes the variance more difficult to compute. Most statistical packages assume that data are collected by a simple random sampling design. Working on the PISA data with these packages would underestimate the standard errors and incorrectly conclude that insignificant results are significant. In fact, there is no available formula to correctly compute the standard error of any estimator from the PISA data.

To solve the estimation problem of standard errors, in addition to a set of final student weights, the PISA data provide 80 sets of replicate weights to compute a sampling variance. It should be recalled that the PISA does not publish students’ original scores, and instead publishes five student plausible values that it imputed. These five plausible values can be used to compute the imputation variance. With five plausible values, one final weight, and 80 replicate weights, to have an unbiased estimator of the standard error, the PISA recommends that researchers conduct any statistical estimation 405 times. For example, in order to have an unbiased standard error of a regression coefficient or a coefficient of a multilevel model, one has to conduct the estimation 405 times, thereby making the estimation process very cumbersome. To save estimation time, the PISA suggests an unbiased shortcut requiring that the estimation be conducted 85 times. This study’s estimation of the multilevel model followed the shortcut methodology (PISA data analysis manual SAS, second edition, 2009, pp. 131–132). The shortcut includes five steps. First, the first plausible value and the final student weight is used to conduct an estimation of the multilevel model to obtain $$\hat{\beta }_{1} $$ . Similarly, the first plausible value and 80 replicate weights are used to conduct the estimation 80 times, and obtain 80 $$\hat{\beta }_{{(i)}} $$ , i=1,…, 80. The sampling variance is computed by Fay’s variant of the Balanced Repeated Replicate as follows:

$$\hat{\sigma }_{{(\hat{\beta })}}^{2} \,{\equals}\,{1 \over {80(1{\minus}0.5)^{2} }}\mathop{\sum}\limits_{{\rm i}\,{\equals}\,1}^{80} ( \hat{\beta }_{{{\rm (i)}}} {\minus}\hat{\beta }_{1} )^{2} .$$

The other four plausible values and the final student weight are used to conduct the estimation four times and obtain $$\hat{\beta }_{2} $$ , $$\hat{\beta }_{3} $$ , $$\hat{\beta }_{4} $$ and $$\hat{\beta }_{5} $$ .Then $$\hat{\beta }$$ is computed as:

$$\hat{\beta }\,{\equals}\,\mathop{\sum}\nolimits_{j\,{\equals}\,1}^5 {\hat{\beta }_{j} } \,/\,5.$$

The imputation variance is computed as:

$$\hat{\sigma }_{{(\rm impute)}}^{2} \,{\equals}\,{1 \over 4}\mathop{\sum}\limits_{i\,{\equals}\,1}^5 ( \hat{\beta }_{j} {\minus}\hat{\beta })^{2} .$$

The final error variance is computed as

$$\hat{\sigma }_{{(\rm error)}}^{2} \,{\equals}\,\hat{\sigma }_{{(\hat{\beta })}}^{2} {\plus}(1{\plus}{\textstyle{1 \over M}})\hat{\sigma }_{{({\rm impute})}}^{2} \,{\equals}\,\hat{\sigma }_{{(\hat{\beta })}}^{2} {\plus}1.2\hat{\sigma }_{{({\rm impute})}}^{2},$$

where M is the number of plausible values.

Individual data are used to investigate the relationship between the gender gap in mathematics and gender equality. The PISA data set is typically hierarchical, and a three-level multilevel model provides the most appropriate fit to the data. The first level is the student (i), the second level is the school (j) and the third level is the country (k). By substituting the level-2 and level-3 models into the level-1 model, the mixed model is derived.

Level 1 Model (student)

$$\eqalignno { {\rm PV}_{{ijk}} \,{\equals}\,& \pi _{{0jk}} {\plus}\pi _{{1jk}} {\rm Female}_{{ijk}} {\plus}\mathop{\sum}\nolimits_{s\,{\equals}\,2}^6 {\pi _{{2{\rm jk}}}^{s} {\rm FISCED}_{{ijk}}^{s} } {\rm }{\plus}\mathop{\sum}\nolimits_{s\,{\equals}\,2}^6 {\pi _{{3jk}}^{s} {\rm MISCED}_{{ijk}}^{s} } \cr & {\plus}\pi _{{4jk}} {\rm HISEI}_{{ijk}} {\plus}e_{{ijk}} $$

Level 2 Model (school)

$$\eqalignno{ & \pi _{{0jk}} \,{\equals}\,\beta _{{00k}} {\plus}r_{{0jk}} \cr & \pi _{{1jk}} \,{\equals}\,\beta _{{10k}} {\plus}\beta _{{11k}} {\rm FP}_{{jk}} \cr & \pi _{{2jk}}^{s} \,{\equals}\,\beta _{{20k}}^{s} ,\,s\,{\equals}\,2,\,3,\,\ldots{\!}{\!},\,6 \cr & \pi _{{3jk}}^{s} \,{\equals}\,\beta _{{30k}}^{s} ,\,s\,{\equals}\,2,\,3,\,\ldots{\!}{\!},\,6 \cr & \pi _{{4jk}} \,{\equals}\,\beta _{{40k}} $$

Level 3 Model (country)

$$\eqalignno{ & \beta _{{00k}} \,{\equals}\,\gamma _{{000}} {\plus}u_{{00k}} \cr & \beta _{{10k}} \,{\equals}\,\gamma _{{100}} {\plus}\gamma _{{101}} {\rm GGI}_{k} \cr & \beta _{{11k}} \,{\equals}\,\gamma _{{110}} \cr & \beta _{{20k}}^{s} \,{\equals}\,\gamma _{{200}}^{s} ,\,s\,{\equals}\,2,\,3,\,\,\ldots{\!}{\!},\,6 \cr & \beta _{{40k}}^{s} \,{\equals}\,\gamma _{{300}}^{s} ,\,s\,{\equals}\,2,\,3,\,\,\ldots{\!}{\!},\,6 \cr & \beta _{{40k}} \,{\equals}\,\gamma _{{400}} $$

Mixed Model

$$\eqalignno{ PV_{{ijk}} \,{\equals}\, & \gamma _{{000}} {\plus}\gamma _{{001}} {\rm GGI}_{k} {\plus}\gamma _{{100}} {\rm Female}_{{ijk}} {\plus}\mathop{\sum}\nolimits_{s\,{\equals}\,2}^6 {{\rm \gamma }_{{200}}^{s} {\rm FISCED}_{{{\rm ijk}}}^{s} } {\plus}\mathop{\sum}\nolimits_{s\,{\equals}\,2}^6 {\gamma _{{300}}^{s} {\rm MISCED}_{{ijk}}^{s} } \cr & {\plus}\gamma _{{400}} {\rm HISEI}_{{ijk}} {\plus}\gamma _{{101}} {\rm Female}_{{ijk}} {\rm GGI}_{k} {\plus}\gamma _{{110}} {\rm Female}_{{ijk}} {\rm FP}_{{jk}} {\plus}r_{{0jk}} {\plus}u_{{00k}} {\plus}e_{{ijk}} . $$

In the first level, FISCED and MISCED are the educational levels of the student’s father and mother, respectively. The superscript ‘s’ denotes the educational level, and the first letters F and M respectively denote father and mother. Both educational level indexes were classified using the ISCED (International Standard Classification of Education, OECD, 1999), which consists of seven categories of educational qualification, and the lowest level (None) and the primary education (ISCED 1) were the reference groups. The educational qualifications for the seven categories were: (1) None and ISCED 1 (primary education); (2) ISCED 2 (lower secondary); (3) ISCED Levels 3B or 3C (vocational/pre-vocational upper secondary); (4) ISCED 3A (upper secondary) and/or ISCED 4 (non-tertiary post-secondary); (5) ISCED 5B (vocational tertiary); and (6) ISCED 5A, 6 (theoretically oriented tertiary and postgraduate).

The PISA surveys occupational data for both the student’s father and mother by asking open-ended questions. Students’ answers are coded into four-digit ISCO codes (International Labour Organization, ILO, 1990) and then mapped to the international socioeconomic index of occupational status (ISEI) (Ganzeboom et al., 1992), and a higher ISEI score corresponds to a higher level of occupational status. The highest occupational status of parents (HISEI) denotes the higher ISEI score of either parent or the only available parent’s ISEI score. In the second level, FP is the ratio of females for a school. The GGI is a country-level explanatory variable and π, β and γ are coefficients, while e, r and u are the random terms. The terms π _0jk and β _00k are random coefficients. From the mixed model, it becomes more clear that it is the sign and the significance of γ ₁₀₁ that are of interest.

Results and Discussions

Country-level data

Table 2 presents the results of the OLS and panel data models, eqns (1) to (3). The upper part of Table 2 shows the OLS results. The bottom panel of Table 2 presents only the results of the fixed-effects models, since the Hausman tests favour the fixed-effects models. The OLS results show that GGI has a negative relationship with the gender difference in mathematics. Of particular note is that the coefficient of GGI from the 2003-based countries is the most significant and greatest in terms of absolute value. However, this relationship vanishes as the data are applied to the panel data models. The results of the OLS, together with the results of the panel data models, indicate that this relationship exists across countries, but does not exist in a given country. That is, compared with a gender-unequal country, although a more gender-equal country is associated with a lower gender gap in mathematics, the gender gap in mathematics is not significantly correlated with the degree of gender equality in a given country. Consequently, the improvement in gender equality in a given country cannot guarantee a decline in the gender gap in mathematics. In addition to GGI, both SEATS and FLFP are either insignificant in the OLS models or significant at the opposite sign in the panel data models. The coefficients of FLFP in the panel data models are significantly positive, contradicting the hypothesis that the more that women participate in the labour market, the lower the boys’ superiority in mathematics in that country is. As the coefficients of GDP are significantly positive in the OLS models, these unexpected results might be due to multicollinearity since GGI is constructed from SEATS and FLPR, which are correlated with GDP.

Table 2 Multiple regression results of all PISA waves based on different country samples

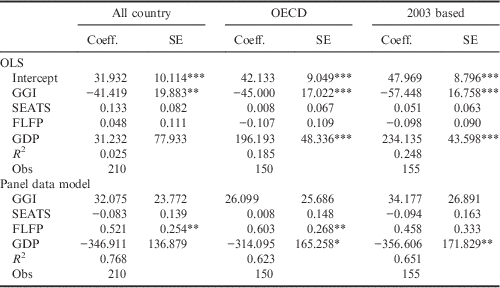
The dependent variable is the national mean gender gap in mathematics. SE is the standard error of a coefficient. GGI is the global Gender Gap Index. SEATS and FLPR represent the proportion of seats held by women in the parliament and the female labour participation rate, respectively. GDP is measured in million dollars. The 2003-based sample indicates that only countries sampled in PISA 2003 were considered in the other waves. In the panel data model, the Hausman test favours the fixed-effects models. Therefore, only the results of the fixed-effects models are reported.

*p<0.1; **p<0.05; ***p<0.01.

To explore the relationship between the gender equality indicator and the gender gap in mathematics without being bothered by possible multicollinearity, and to compare the results with those in the literature, each model in Table 3 includes only one explanatory variable. Table 3 shows the results of the OLS and the panel data models for these three country samples. In the OLS results, the coefficients of GGI are negative and significant, at least at the 10% level. In the OECD sample, all three gender equality indicators (GGI, SEATS, FLPR) are negative and significant at the 1% level, indicating that the inclusion of only one explanatory variable might mitigate the multicollinearity problem in Table 2. Similar to Table 2, these negative correlations disappear in Table 3 when country fixed effects are taken into account. Consequently, a consistent conclusion is reached with Table 2. The cross-sectional country samples display a negative correlation, but this negative relationship disappears in the longitudinal country samples.

Table 3 Simple regression results of all PISA waves based on different country samples

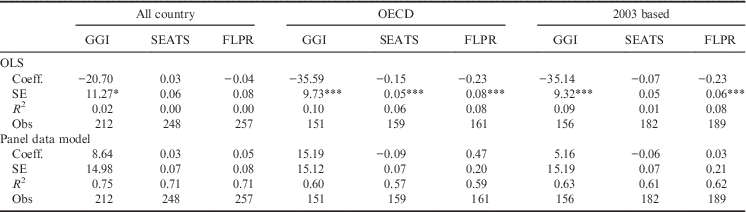
The dependent variable is the national mean gender gap in mathematics. SE is the standard error of a coefficient. Each simple regression has an intercept that is not shown. See the footnote to Table 2 for the definitions of GGI, SEATS, FLPR and 2003 based.

*p<0.1; ***p<0.01.

Annual cross-sectional country samples were used to explore the relationship between gender equality and the gender gap in mathematics. As in the case of the models in Table 3, all models in Table 4 include only one explanatory variable, and are estimated under three different country samples. Interestingly, when using the all-country sample, the coefficients of GGI are negative and significant in 2000 and 2003, but are insignificant after 2003. All these three gender equality indicators are simultaneously negative and significant in 2003, but are not simultaneously significant in the other years. The results for the OECD and the 2003-based samples are similar to those for the all-country sample, except in the case of PISA 2012. In 2012, GGI and FLPR again turn out to be significant.

Table 4 Simple regression results of single PISA wave based on different gender equality indices

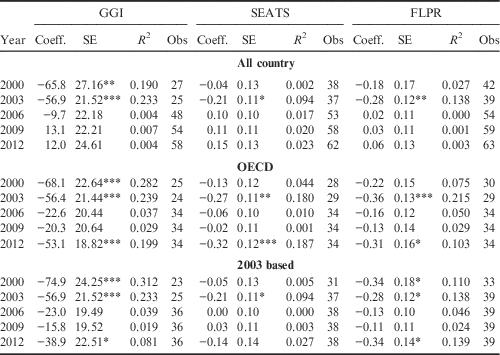
The dependent variable is the national mean gender gap in mathematics. SE is the standard error of a coefficient. Each simple regression has an intercept which is not shown. See the footnote to Table 2 for the definitions of other abbreviations.

*p<0.1; **p<0.05; ***p<0.01.

These results are consistent with those of Guiso et al. (2008) and Else-Quest et al. (2010), who used PISA 2003 to show a negative correlation between the gender equality indicators and the gender gap in mathematics. However, this study provides a more complete picture regarding the negative correlation between gender equality and the gender gap in mathematics. First, the negative correlation has not persisted after 2003 when more countries joined the PISA. Second, this negative correlation appeared again in 2012, but the correlation only applied to the small country sample, the OECD or the 2003-based countries. Table 4 illustrates that this relationship never appeared as the number of countries is greater than or equal to 48. From analysing the country-level data, it is concluded that the relationship between gender equality and the gender gap in mathematics might exist in a small cross-sectional country sample, but this relationship cannot be extended to a large country sample. To sum up, the relationship between gender equality and the gender gap in mathematics found by the previous studies is not found in a given country, cannot be extended to samples including more countries, and has not persistently occurred annually, even for the same country sample.

Individual-level data

The results of the three-level multilevel models for the all-country sample of PISA 2012 are presented in Table 5. To examine how gender equality is correlated with the females’ performance in mathematics, an interaction term made up of GGI and Female was incorporated into the models. The coefficients of Female are all negative, and are significant when either GGI or GGI×Female is not in the models. The Female coefficient is extremely significant when GGI×Female is excluded. The significantly positive coefficient of GGI suggests that gender equality is associated with mathematics performance. The coefficients of GGI×Female are not significant in Models II and III. Although gender equality is correlated with mathematics performance, females in a gender-equal country do not score more highly. As a result, gender equality is not correlated with the gender gap in mathematics for the all-country sample of PISA 2012.

Table 5 Results of three-level multilevel models for PISA 2012, all-country sample

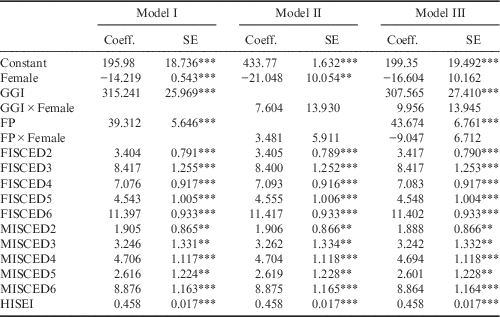
The dependent variable is the plausible value. SE is the standard error of a coefficient. The sample includes 388,561 students, 15,976 schools and 55 countries. FP is the ratio of females for a school. HISEI is based on the international socioeconomic index of occupational status (ISEI), and denotes the highest occupational status of parents. Fathers’ and mothers’ educational attainment (FISCED and MISCED) are based on the ISCED (International Standard Classification of Education, OECD, 1999), which consists of seven categories of educational qualification, and the lowest level (None) and primary education (ISCED1) are the reference groups.

**p<0.05; ***p<0.01.

In addition, Else-Quest et al. (2010) indicated that the stereotype threat is increased if girls are outnumbered by boys in an environment. Consequently, the proportion of girls in school (FP) is used to examine the effect of stereotype threat. The proportion of girls in school is positively correlated with the students’ performance in mathematics, but girls in a school with a high proportion of girls did not score more highly in mathematics. Both the fathers’ and mothers’ educational attainments are helpful to the students’ performances in mathematics, while the fathers’ educational attainment is more important than the mothers’. The parents’ occupational status is strongly correlated with the students’ performances in mathematics.

The conclusion on the relationship between gender equality and the gender gap in mathematics changes when the countries are restricted to the OECD. Table 6 shows that the GGI is not associated with overall performance in mathematics, but GGI is positively correlated with the females’ performance in mathematics. The inconsistent results of the all-country and OECD samples are in line with the results for the country-level data in Table 4, where GGI is not significant in the all-country sample, but is significantly negative in the OECD sample for PISA 2012. The results for the individual data and the country-level data are consistent for PISA 2012.

Table 6 Results of three-level multilevel models for PISA 2012, OECD countries

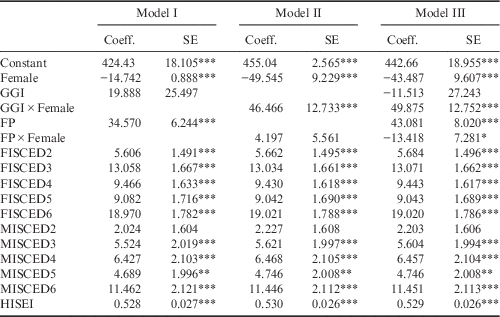
The dependent variable is the plausible value. SE is the standard error of a coefficient. The sample includes 262,006 students, 10,902 schools and 33 countries. FP is the ratio of females for a school. HISEI is based on the international socioeconomic index of occupational status (ISEI), and denotes the highest occupational status of parents. Fathers’ and mothers’ educational attainment (FISCED and MISCED) are based on the ISCED (International Standard Classification of Education, OECD, 1999), which consists of seven categories of educational qualification, and the lowest level (None) and primary education (ISCED1) are the reference groups.

*p<0.1; **p<0.05; ***p<0.01.

Conclusion

Some researchers have argued that the gender gap in mathematics is generated by stratifying women into occupations with little need for mathematics. Gender stratification is a consequence of gender inequality. Using PISA 2003, Guiso et al. (2008) and Else-Quest et al. (2010) found evidence of a negative relationship between the gender gap in mathematics and gender equality. This study confirms that this negative relationship did exist in the PISA 2003 sample of cross-sectional countries. However, this negative relationship does not persist after 2003 when more countries are included in the PISA. This negative relationship cannot be found in PISA 2006 and PISA 2009, even when the sample countries are restricted to the OECD or the same countries as in PISA 2003. This negative relationship reappears in the PISA 2012 for the OECD sample, but not for the all-country sample. The results from analysing the individual data of PISA 2012 verify the conclusion from the country-level data of PISA 2012.

Although the OLS model exhibits a negative relationship between the gender gap in mathematics and gender equality, by using all five waves of the PISA data, this negative relationship vanishes when the panel data models are used. The insignificant results of the panel data models, along with the significant results of the OLS models, imply that this negative relationship might exist across countries but that it does not exist in a given country. Consequently, the significant results of the cross-sectional country-level data cannot endorse the position that an improvement in gender equality accompanies an improvement in the gender gap in mathematics in a given country.