1 Introduction
In countries of all income levels there is a wide belief that health insurance has tremendous value, a belief that underpins inclusion of universal health coverage (UHC) in the ‘sustainable development goals’ for all countries by 2030.Footnote 1 In valuing the benefits of health insurance, most analyses, not surprisingly, focus primarily on its beneficial impact on health (Jamison et al., Reference Jamison, Summers, Alleyne, Arrow, Berkley and Binagwaho2013; Robinson et al., Reference Robinson, Hammitt, Jamison and Walker2019a ,Reference Robinson, Hammitt and O’Keeffe b ). Yet researchers and policy analysts have understood for many years that insurance also protects against major shocks to the financial well-being of the household by mitigating lost earning capacity, and helping to cover out-of-pocket health care expenditures (Arrow, Reference Arrow1963; Zeckhauser, Reference Zeckhauser1970; Baily, Reference Baily1978; Feldman & Dowd, Reference Feldman and Dowd1991; Gertler & Gruber, Reference Gertler and Gruber2002; Wagstaff & van Doorslaer, Reference Wagstaff and van Doorslaer2003; Chetty, Reference Chetty2006; van Doorlsaer et al., Reference van Doorlsaer, O’Donnell, Rannan-Eliya, Somanathan and Adhikari2006, Reference van Doorlsaer, O’Donnell, Rannan, Aparnaa and Shiva2007; Wagstaff, Reference Wagstaff, Smith, Mossialos and Papanicolas2010; Baicker & Levy, Reference Baicker and Levy2012; Smith, Reference Smith2013; Flores & O’Donnell, Reference Flores and O’Donnell2016). Indeed, when President Lyndon Johnson in the U.S. enacted the Medicare program to cover the elderly, in 1965, he declared “No longer will illness crush and destroy the savings that [older Americans] have so carefully put away over a lifetime so that they might enjoy dignity in their later years” (Baicker & Levy, Reference Baicker and Levy2012).
Despite the general recognition that health insurance is valuable for more than “buying health” (as in Nyman (Reference Nyman1999); see also Jan et al. (Reference Jan, Laba, Essue, Gheorghe and Muhunthan2018)), placing a monetary value on the financial benefits of health insurance in benefit-cost analysis is less commonly done. One exception is Verguet et al. (Reference Verguet, Laxminarayan and Jamison2015), who used an “extended cost-effectiveness analysis” (ECEA) framework to estimate the financial benefits of a universal public insurance program for tuberculosis treatment, and found substantial benefits, particularly to the lowest quintile of the income distribution. Earlier examples include Gertler and Gruber (Reference Gertler and Gruber2002) who examined financial risk in Indonesia, and McClellan and Skinner (Reference McClellan and Skinner2006), who estimated that the financial benefits of the U.S. Medicare program were as much as 88 cents per dollar of insurance coverage (also see Finkelstein & McKnight, Reference Finkelstein and McKnight2008). The benefits of expanding insurance coverage, and the pathways through which those benefits can be realized, are multidimensional as is shown in Figure 1.

Figure 1 Financial risk protection aspects of health insurance. Source: Jamison et al. (Reference Jamison, Alwan, Mock, Nugent, Watkins and Adeyi2018).
In this paper, we follow the earlier literature in developing a simple two-period model that provides a structure to understand the non-health benefits, and costs, of expanding health insurance. We document how health insurance can have other far-ranging effects on individuals, and society, depending on the design of the proposed insurance policy, and characteristics of the existing health care system. Our goal is to develop simple principles to augment benefit-cost analysis (BCA) and cost-effectiveness analysis (CEA) to capture how health insurance expansion affects financial security for low- and middle-income countries (LMICs) (Jamison, Reference Jamison, Detels, McEwen, Beaghole, Lansang and Gulliford2009). The model allows for different types of insurance coverage, allowing us to address at a theoretical level the value of “broad” coverage of primary care including vaccines and other preventive measures, versus “deep” coverage of costly hospitalizations arising from (e.g.) chronic diseases or catastrophic health events. This analysis constitutes an example of a broader trend to augment cost-effectiveness analysis not only with considerations of financial protection but also of other dimensions of outcome imperfectly captured by standard approaches to CEA and BCA (Phelps et al., Reference Phelps, Lakdawalla, Basu, Drummond, Towse and Danzon2018).
What are the financial effects of health insurance? First, as noted above, it pools the risk of unexpected medical expenditures between healthy and sick households. Second, it can (but may not always) facilitate the redistribution of income from high- to low-income recipients, and by doing so can make previously unattainable health care affordable (Nyman, Reference Nyman1999). Third, it can also facilitate the smoothing of consumption over time; health shocks often come toward the end of life, and so paying early-on through payroll contributions, for example, help to lessen the shock of having to scale back on consumption later in life if health insurance premiums rise with age.
How should these characteristics of health insurance be measured and implemented in benefit-cost analysis? We provide a practical evaluation of health insurance expansions by using an illustrative example from a hypothetical LMIC. Using plausible parameters, the calculations suggest quite large benefits of risk reduction for lower-income groups. Consumption-smoothing benefits are smaller in magnitude but can potentially provide a sizeable proportional benefit to lower-income enrollees but a larger (dollar) benefit to higher-income taxpayers; still, we estimate that adjusting for these combined financial effects tend to make health insurance expansions more progressive. This paper thus contributes to a project to develop a “reference case” for benefit-cost analysis of investments in low- and middle-income countries that have significant health consequences; see Robinson et al. (Reference Robinson, Hammitt, Jamison and Walker2019a ) for an overview of the overall project.
2 The model
We begin with a simple two-period model based on McClellan and Skinner (Reference McClellan and Skinner2006), in which individuals consume non-medical goods in both periods and are subject to the risk of poor health in the second, so that they divide resources in the second period between out-of-pocket medical spending and non-medical consumption. Given the intrinsic uncertainty about future health, we characterize expected utility for individual or household in income group
![]() $j$
,
$j$
,
![]() $W_{j}$
, as being the expected value of lifetime utility:Footnote
2
$W_{j}$
, as being the expected value of lifetime utility:Footnote
2
where the second-period utility (or value) function, which depends on assets at the outset of period 2,
![]() $A_{2j}$
and income received in period 2, Y
$A_{2j}$
and income received in period 2, Y
![]() $_{2j}$
, is written:
$_{2j}$
, is written:
Utility in the first (healthy) period depends on non-medical consumption
![]() $C_{1j}$
, while the value function in the second period – essentially the expected value of utility in period 2 (from the perspective of period 2) depends on the likelihood of surviving to period 2 (
$C_{1j}$
, while the value function in the second period – essentially the expected value of utility in period 2 (from the perspective of period 2) depends on the likelihood of surviving to period 2 (
![]() $\unicode[STIX]{x1D70B}$
) and the time preference rate
$\unicode[STIX]{x1D70B}$
) and the time preference rate
![]() $\unicode[STIX]{x1D6FF}$
. Once arriving at period 2, there is a chance of bad health,
$\unicode[STIX]{x1D6FF}$
. Once arriving at period 2, there is a chance of bad health,
![]() $\unicode[STIX]{x1D70B}_{b}$
, and good health,
$\unicode[STIX]{x1D70B}_{b}$
, and good health,
![]() $\unicode[STIX]{x1D70B}_{g}$
; because the individual has survived to period 2, the two probabilities sum to one.Footnote
3
$\unicode[STIX]{x1D70B}_{g}$
; because the individual has survived to period 2, the two probabilities sum to one.Footnote
3
The input
![]() $h_{2j}$
is the component of health care that corresponds to clinics, vaccinations, and other relatively low-cost treatments that are assumed to be the same whether the individual is in good or poor health; it is less likely to impose catastrophic costs on recipients. However, this input is assumed to have an impact on the likelihood of being in the healthy or sick state of the world, so we assume that
$h_{2j}$
is the component of health care that corresponds to clinics, vaccinations, and other relatively low-cost treatments that are assumed to be the same whether the individual is in good or poor health; it is less likely to impose catastrophic costs on recipients. However, this input is assumed to have an impact on the likelihood of being in the healthy or sick state of the world, so we assume that
![]() $0>d\unicode[STIX]{x1D70B}_{b}/dh_{2j}=-d\unicode[STIX]{x1D70B}_{g}/dh_{2j}$
.Footnote
4
$0>d\unicode[STIX]{x1D70B}_{b}/dh_{2j}=-d\unicode[STIX]{x1D70B}_{g}/dh_{2j}$
.Footnote
4
The budget constraint from the perspective of period 2 is:
The government’s budget constraint in period 2, which consists of income-based tax revenue devoted to health care,
![]() $P(Y)$
, is given by:
$P(Y)$
, is given by:
 $$\begin{eqnarray}\left[G_{2}+\mathop{\sum }_{j}n_{j}[\unicode[STIX]{x1D70B}_{g}P(Y_{2gj})+\unicode[STIX]{x1D70B}_{b}P(Y_{2bj})]\right]-\mathop{\sum }_{j}n_{j}[\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6F7}+h_{2j}\unicode[STIX]{x1D711}]=0,\end{eqnarray}$$
$$\begin{eqnarray}\left[G_{2}+\mathop{\sum }_{j}n_{j}[\unicode[STIX]{x1D70B}_{g}P(Y_{2gj})+\unicode[STIX]{x1D70B}_{b}P(Y_{2bj})]\right]-\mathop{\sum }_{j}n_{j}[\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6F7}+h_{2j}\unicode[STIX]{x1D711}]=0,\end{eqnarray}$$
where the government collects user fees from the current (older) generation through the tax and premium mechanism
![]() $P(Y)$
, and
$P(Y)$
, and
![]() $n_{j}$
is the fraction of income group
$n_{j}$
is the fraction of income group
![]() $j$
in the overall economy. Note that there is an additional source of revenue
$j$
in the overall economy. Note that there is an additional source of revenue
![]() $G_{2}$
, which can (in a life-cycle framework) come from the current older generation contributing to a social insurance fund during their earlier working years in period 1 (with an annuity return of those who died between periods 1 and 2),
$G_{2}$
, which can (in a life-cycle framework) come from the current older generation contributing to a social insurance fund during their earlier working years in period 1 (with an annuity return of those who died between periods 1 and 2),
![]() $G_{2}=\sum _{j}[P_{1}(Y_{1j})(1+r+\unicode[STIX]{x1D70B})n_{j}]$
. Alternatively, one could posit that the budget is for the current year, in which case
$G_{2}=\sum _{j}[P_{1}(Y_{1j})(1+r+\unicode[STIX]{x1D70B})n_{j}]$
. Alternatively, one could posit that the budget is for the current year, in which case
![]() $G_{2}$
would come from taxes paid concurrently by the younger generation.
$G_{2}$
would come from taxes paid concurrently by the younger generation.
To capture the idea that benefit expansion can subsidize different types of health care expenditures, we consider two insurance coverage rates; the first,
![]() $\unicode[STIX]{x1D6F7}$
, is for expenditures on
$\unicode[STIX]{x1D6F7}$
, is for expenditures on
![]() $H_{2}$
, which we characterize as “tertiary” or more intensive care (often associated with hospitalization); for simplicity we assume these expenditures are incurred only in the bad state of health, and do not provide direct utility benefit.Footnote
5
The second insurance coverage rate for
$H_{2}$
, which we characterize as “tertiary” or more intensive care (often associated with hospitalization); for simplicity we assume these expenditures are incurred only in the bad state of health, and do not provide direct utility benefit.Footnote
5
The second insurance coverage rate for
![]() $h_{2},\unicode[STIX]{x1D711}$
, may differ, depending on whether the insurance system is focused on covering primary care or catastrophic care.Footnote
6
$h_{2},\unicode[STIX]{x1D711}$
, may differ, depending on whether the insurance system is focused on covering primary care or catastrophic care.Footnote
6
The first two budget constraints express second-period consumption depending on whether the individual ends up in a good or bad state of the world. For simplicity, we ignore the savings decision in period 1, to which we return below; thus the model simplifies to the second period conditional on assets
![]() $A_{2j}$
saved from period 1. The value of insurance is twofold; first for the h-component of spending, to improve health and thus the likelihood of being in the good or healthy state of the world, which has additional beneficial effects on aggregate income and tax revenue. The second is by subsidizing out-of-pocket spending for
$A_{2j}$
saved from period 1. The value of insurance is twofold; first for the h-component of spending, to improve health and thus the likelihood of being in the good or healthy state of the world, which has additional beneficial effects on aggregate income and tax revenue. The second is by subsidizing out-of-pocket spending for
![]() $H_{2}$
, catastrophic health, it cushions the financial blow and implicitly narrows the consumption downturn between
$H_{2}$
, catastrophic health, it cushions the financial blow and implicitly narrows the consumption downturn between
![]() $C_{2b}$
and
$C_{2b}$
and
![]() $C_{2g}$
. Of course, these programs are not free; individuals must pay for either or both programs through the income-dependent payment schedule
$C_{2g}$
. Of course, these programs are not free; individuals must pay for either or both programs through the income-dependent payment schedule
![]() $P(Y)$
.
$P(Y)$
.
In this section, we consider the incremental financial benefits of expanding specific health insurance coverage (and thus do not focus on measuring the health benefit of spending on
![]() $h_{2}$
). We provide a framework for approximating benefits and costs, recognizing that in practice the measurement will depend very much on the individual country characteristics. To do this, we employ a first-order Taylor-series approximation of the utility function in period 2:
$h_{2}$
). We provide a framework for approximating benefits and costs, recognizing that in practice the measurement will depend very much on the individual country characteristics. To do this, we employ a first-order Taylor-series approximation of the utility function in period 2:
and we drop the
![]() $j$
th (income) subscript for now. To allow for convenient numerical estimates, it is useful to assume further a commonly used utility function that exhibits constant relative risk aversion, so that
$j$
th (income) subscript for now. To allow for convenient numerical estimates, it is useful to assume further a commonly used utility function that exhibits constant relative risk aversion, so that
![]() $U(C)=C^{1-\unicode[STIX]{x1D6FE}}/1-\unicode[STIX]{x1D6FE}$
where
$U(C)=C^{1-\unicode[STIX]{x1D6FE}}/1-\unicode[STIX]{x1D6FE}$
where
![]() $\unicode[STIX]{x1D6FE}$
is the Arrow–Pratt coefficient of relative risk aversion (CRRA). We can therefore rearrange equation (3), and express the change in utility in “money-metric” monetary (e.g., in terms of renminbi, dollar, or peso) terms, evaluated in the healthy or good state of the world
$\unicode[STIX]{x1D6FE}$
is the Arrow–Pratt coefficient of relative risk aversion (CRRA). We can therefore rearrange equation (3), and express the change in utility in “money-metric” monetary (e.g., in terms of renminbi, dollar, or peso) terms, evaluated in the healthy or good state of the world
![]() $\unicode[STIX]{x1D6E5}M\equiv \unicode[STIX]{x1D6E5}V/U^{\prime }(C_{g2})$
as the following:
$\unicode[STIX]{x1D6E5}M\equiv \unicode[STIX]{x1D6E5}V/U^{\prime }(C_{g2})$
as the following:
where
![]() $\unicode[STIX]{x1D703}$
is the ratio of marginal utilities in the good and bad states of the world. Using the CRRA assumption, this allows us to write
$\unicode[STIX]{x1D703}$
is the ratio of marginal utilities in the good and bad states of the world. Using the CRRA assumption, this allows us to write
![]() $\unicode[STIX]{x1D703}$
as depending on the (initial) difference in consumption in the good and bad states of the world:
$\unicode[STIX]{x1D703}$
as depending on the (initial) difference in consumption in the good and bad states of the world:
![]() $\unicode[STIX]{x1D703}=[C_{2g}/C_{2b}]^{\unicode[STIX]{x1D6FE}}$
. For
$\unicode[STIX]{x1D703}=[C_{2g}/C_{2b}]^{\unicode[STIX]{x1D6FE}}$
. For
![]() $\unicode[STIX]{x1D6FE}=3$
, a commonly used measure of relative risk aversion, and a consumption gap arising both from out-of-pocket expenditures, and differences in consumption of (say) 40%, or
$\unicode[STIX]{x1D6FE}=3$
, a commonly used measure of relative risk aversion, and a consumption gap arising both from out-of-pocket expenditures, and differences in consumption of (say) 40%, or
![]() $\unicode[STIX]{x1D703}=1.4^{3}=2.7$
the extent to which one would upweight an increase of $1 in the bad state of the world relative to an increase of $1 in the good state of the world. When
$\unicode[STIX]{x1D703}=1.4^{3}=2.7$
the extent to which one would upweight an increase of $1 in the bad state of the world relative to an increase of $1 in the good state of the world. When
![]() $\unicode[STIX]{x1D6FE}=1.5$
, so that individuals are less risk-averse, the value of insurance is still considerable;
$\unicode[STIX]{x1D6FE}=1.5$
, so that individuals are less risk-averse, the value of insurance is still considerable;
![]() $1.4^{1.5}=1.7$
. This focus on the ratio of marginal utilities in the different states of the world is quite general to the model specification and other characteristics of risk-sharing in the economy (Baily, Reference Baily1978; Gertler & Gruber, Reference Gertler and Gruber2002; Chetty, Reference Chetty2009).
$1.4^{1.5}=1.7$
. This focus on the ratio of marginal utilities in the different states of the world is quite general to the model specification and other characteristics of risk-sharing in the economy (Baily, Reference Baily1978; Gertler & Gruber, Reference Gertler and Gruber2002; Chetty, Reference Chetty2009).
Using our example above, how might one evaluate an actuarially fair expansion of health insurance that raises health insurance coverage for catastrophic care? The per-person cost to the government is (to a first-order approximation)
![]() $\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
. Everyone (in both good and bad health) thus pays an extra premium of
$\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
. Everyone (in both good and bad health) thus pays an extra premium of
![]() $\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
. Then
$\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
. Then
![]() $\unicode[STIX]{x1D6E5}C_{2gj}=-\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
, and
$\unicode[STIX]{x1D6E5}C_{2gj}=-\unicode[STIX]{x1D70B}_{b}H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
, and
![]() $\unicode[STIX]{x1D6E5}C_{2b}=(1-\unicode[STIX]{x1D70B}_{b})H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
, so that
$\unicode[STIX]{x1D6E5}C_{2b}=(1-\unicode[STIX]{x1D70B}_{b})H_{2}\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6F7}$
, so that
Note that the left-hand side of the equation is capturing the incremental increase in money-metric utility per dollar increase in the premium for the expanded health insurance. The result indicates that, if there were no need for risk-pooling, in the sense that consumption in both states of the world are equal, then there would be no net social benefit from risk reduction. However, in the example we considered before, where a 40% consumption gap is certainly possible (e.g., Xu et al., Reference Xu, Evans, Kawabata, Zeramdini, Klavus and Murray2003; Jan et al., Reference Jan, Laba, Essue, Gheorghe and Muhunthan2018), the net financial benefit to society from risk-pooling is roughly
![]() $1.7\unicode[STIX]{x1D70B}_{g}$
incremental dollars per dollar increase in the premium.Footnote
7
$1.7\unicode[STIX]{x1D70B}_{g}$
incremental dollars per dollar increase in the premium.Footnote
7
This is of course a simplification; it does not capture additional complexities introduced if the marginal utility of consumption differs in the sick and healthy state (Finkelstein et al., Reference Finkelstein, F. P. Luttmer and Notowidigdo2013), nor does it account for efficiencies or inefficiencies associated with paying for insurance through taxation, or with moral hazard and adverse selection issues. Nor can this approximation be used in the case of a fundamental change in health insurance, where the incremental measure could overstate the full general-equilibrium benefits of premium increases; we suggest a modification to approximate global effects below. Nonetheless, this approach provides a first-order estimate of the financial benefits associated with a reduction in risk.
The second aspect of health insurance is its redistributive component. In this case, we consider high-income (
![]() $j=r$
) and low-income (
$j=r$
) and low-income (
![]() $j=p$
) households, and with premiums that reflect their different income status. A simple example of redistribution arises when the
$j=p$
) households, and with premiums that reflect their different income status. A simple example of redistribution arises when the
![]() $P(Y)$
function becomes more progressive, so that higher-income enrollees pay more, and lower-income enrollees pay less, holding revenue constant. In this case, the introduction of UHC will have first-order effects on the tax and premium collections by income group; these of course should be measured to evaluate the extent of redistribution across incomes.
$P(Y)$
function becomes more progressive, so that higher-income enrollees pay more, and lower-income enrollees pay less, holding revenue constant. In this case, the introduction of UHC will have first-order effects on the tax and premium collections by income group; these of course should be measured to evaluate the extent of redistribution across incomes.
While we are not explicitly considering health outcomes in this paper, we do note that consumption in high- and low-income groups (and hence the degree of income inequality), and the degree to which they previously purchased health care in private markets, matter in assessing the distributional effects of health insurance expansion. For example, suppose that initially
![]() $\unicode[STIX]{x1D711}=0$
, so there was an entirely private market for
$\unicode[STIX]{x1D711}=0$
, so there was an entirely private market for
![]() $h_{2}$
. We would expect that when solving for (1b
) and equations (2a
)–(2c
), that
$h_{2}$
. We would expect that when solving for (1b
) and equations (2a
)–(2c
), that
![]() $h_{2r}$
for high-income households would exceed
$h_{2r}$
for high-income households would exceed
![]() $h_{2p}$
for low-income households, given that the demand for health care is greater among high-income households.
$h_{2p}$
for low-income households, given that the demand for health care is greater among high-income households.
Suppose that the new policy initiative is to provide full coverage for
![]() $h_{2}$
, and as a consequence the use of
$h_{2}$
, and as a consequence the use of
![]() $h_{2}$
rises, by different amounts, for both high- and low-income households. The utilitarian money-equivalent benefits of this improved health are approximated by:
$h_{2}$
rises, by different amounts, for both high- and low-income households. The utilitarian money-equivalent benefits of this improved health are approximated by:
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}M_{p}^{\prime }+\unicode[STIX]{x1D6E5}M_{r}^{\prime } & = & \displaystyle \frac{d\unicode[STIX]{x1D70B}_{g}(h_{2r})}{dh_{2}}\left[\frac{U(C_{2gr})-U(C_{2br})}{U^{\prime }(C_{2gr})}\right]\unicode[STIX]{x1D6E5}h_{2r}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d\unicode[STIX]{x1D70B}_{g}(h_{2p})}{dh_{2}}\left[\frac{U(C_{2gp})-U(C_{2bp})}{U^{\prime }(C_{2gp})}\right]\unicode[STIX]{x1D6E5}h_{2p}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E5}M_{p}^{\prime }+\unicode[STIX]{x1D6E5}M_{r}^{\prime } & = & \displaystyle \frac{d\unicode[STIX]{x1D70B}_{g}(h_{2r})}{dh_{2}}\left[\frac{U(C_{2gr})-U(C_{2br})}{U^{\prime }(C_{2gr})}\right]\unicode[STIX]{x1D6E5}h_{2r}\nonumber\\ \displaystyle & & \displaystyle +\,\frac{d\unicode[STIX]{x1D70B}_{g}(h_{2p})}{dh_{2}}\left[\frac{U(C_{2gp})-U(C_{2bp})}{U^{\prime }(C_{2gp})}\right]\unicode[STIX]{x1D6E5}h_{2p}.\end{eqnarray}$$
While this is a complicated equation, the intuition is straightforward. The first term on the right-hand side of the equation is the value of the incremental
![]() $h_{2}$
for the high-income households, equal to the marginal impact on the probability of good health (evaluated at the initial level of high-income household
$h_{2}$
for the high-income households, equal to the marginal impact on the probability of good health (evaluated at the initial level of high-income household
![]() $h_{2}$
) times the value of incremental utility that captures both health benefits in terms of mortality reduction or disability-adjusted life years (DALYs) or quality-adjusted life years (QALYs), as well as augmented incomes earned in the good state of the world.Footnote
8
The second term is the change in utility arising from better health in the low-income household, again where the marginal health effectiveness is evaluated at their initial level of
$h_{2}$
) times the value of incremental utility that captures both health benefits in terms of mortality reduction or disability-adjusted life years (DALYs) or quality-adjusted life years (QALYs), as well as augmented incomes earned in the good state of the world.Footnote
8
The second term is the change in utility arising from better health in the low-income household, again where the marginal health effectiveness is evaluated at their initial level of
![]() $h_{2}$
. We expect that among low-income households, this marginal effectiveness is larger (that is,
$h_{2}$
. We expect that among low-income households, this marginal effectiveness is larger (that is,
![]() $(d\unicode[STIX]{x1D70B}_{g}(h_{2p})/dh_{2})\geqslant (d\unicode[STIX]{x1D70B}_{g}(h_{2r})/dh_{2})$
) given that poorer households typically begin from a lower-initial level of
$(d\unicode[STIX]{x1D70B}_{g}(h_{2p})/dh_{2})\geqslant (d\unicode[STIX]{x1D70B}_{g}(h_{2r})/dh_{2})$
) given that poorer households typically begin from a lower-initial level of
![]() $h_{2}$
.
$h_{2}$
.
Equation (5) illustrates two aspects of measuring health benefits in the presence of income inequality; the first is well understood, the second less-so. First, the utility benefits for the high-income household is expressed in terms of the inverse of their marginal utility of consumption. Assuming diminishing marginal utility of consumption (consistent with a conventional concave utility function) means that a given difference in health (e.g., in terms of QALYs or DALYs) is weighted more for high-income than for low-income people (with a larger gap in more unequal societies), leading to the implication that saving the life of a high-income individual is worth more than saving the life of a low-income individual (see for example Fleurbaey et al., Reference Fleurbaey, Luchini, Muller and Schokkaert2012; Hammitt, Reference Hammitt2017). Within countries, this is sometimes addressed by implicitly weighting the value of improved health using the same monetary measure across the income distribution; practically this would imply weighting the second term in (5) such that the marginal utility of the low-income individual is equal to that of the high-income individual (where the weight
![]() $\unicode[STIX]{x1D6F9}$
would be chosen so that
$\unicode[STIX]{x1D6F9}$
would be chosen so that
![]() $\unicode[STIX]{x1D6F9}=U^{\prime }(C_{2gp})/U^{\prime }(C_{2gr})$
).
$\unicode[STIX]{x1D6F9}=U^{\prime }(C_{2gp})/U^{\prime }(C_{2gr})$
).
The second issue in measuring benefits of insurance expansion relates to crowding out of private payments. For example, Verguet et al. (Reference Verguet, Laxminarayan and Jamison2015) found that the crowding out of private payments for TB treatment in India would potentially benefit the higher-income groups that were initially able to afford private payment for care. Note that the change in spending
![]() $\unicode[STIX]{x1D6E5}h_{2j}$
for the primary or preventive care can differ by income group, leading to differential health effects by individuals relates to the degree to which health care rises or falls. Yet by making primary care
$\unicode[STIX]{x1D6E5}h_{2j}$
for the primary or preventive care can differ by income group, leading to differential health effects by individuals relates to the degree to which health care rises or falls. Yet by making primary care
![]() $h_{2}$
free to consumers as assumed above (or more generally, by reducing its price), there is a crowding out of private spending that has now been replaced by public spending (Baicker et al., Reference Baicker, Shepard and Skinner2013).
$h_{2}$
free to consumers as assumed above (or more generally, by reducing its price), there is a crowding out of private spending that has now been replaced by public spending (Baicker et al., Reference Baicker, Shepard and Skinner2013).
For example, suppose that the new level of health care spending for high-income households is the same as it was previously. This is a special case that would occur (for example) if capacity constraints on the supply-side limit the quantity of services that can be utilized by high-income households. More generally, there could also be changes in quality-adjusted
![]() $h_{2r}$
, for example if private providers with poor prognostic skills are crowded out, as in Udwadia et al. (Reference Udwadia, Pinto and Uplekar2010), thus raising quality, or if providers skimp following a health insurance expansion, as in Rao (Reference Rao2017), thus reducing quality.Footnote
9
$h_{2r}$
, for example if private providers with poor prognostic skills are crowded out, as in Udwadia et al. (Reference Udwadia, Pinto and Uplekar2010), thus raising quality, or if providers skimp following a health insurance expansion, as in Rao (Reference Rao2017), thus reducing quality.Footnote
9
In this example with no change in
![]() $h_{2r}$
, the high-income household now is receiving the same health benefits as previously at no cost, so they save
$h_{2r}$
, the high-income household now is receiving the same health benefits as previously at no cost, so they save
![]() $h_{2r}$
in out-of-pocket spending. The low-income household would also save
$h_{2r}$
in out-of-pocket spending. The low-income household would also save
![]() $h_{2p}$
, but since
$h_{2p}$
, but since
![]() $h_{2r}>h_{2p}$
, the impact of this health insurance expansion is to expand the potential non-health consumption of high-income households by more than for low-income groups. Of course, this shift can be offset by a sufficient hike in the premiums they pay,
$h_{2r}>h_{2p}$
, the impact of this health insurance expansion is to expand the potential non-health consumption of high-income households by more than for low-income groups. Of course, this shift can be offset by a sufficient hike in the premiums they pay,
![]() $\unicode[STIX]{x1D6E5}P(Y)$
, but without much progressivity in the premium assessments, the net financial effect could be to redistribute from poor to rich, even if the health benefits (e.g., the incremental health spending) are greater for the low-income group. Measuring such distributional effects requires data on out-of-pocket spending by income group, as we consider below in our example.
$\unicode[STIX]{x1D6E5}P(Y)$
, but without much progressivity in the premium assessments, the net financial effect could be to redistribute from poor to rich, even if the health benefits (e.g., the incremental health spending) are greater for the low-income group. Measuring such distributional effects requires data on out-of-pocket spending by income group, as we consider below in our example.
The third way in which expanded coverage can improve lifetime utility is by smoothing consumption over the life cycle by encouraging pre-payment of insurance premiums (e.g., Xu et al., Reference Xu, Evans, Carrin, Mylena, Aguilar-Rivera and Evans2007). To see this, we step back to our two-period model, where the intertemporal first-order condition for consumption can be written (again suppressing the
![]() $j$
th subscript)
$j$
th subscript)
This will hold whether there is insurance or not; for utility functions (such as CRRA) exhibiting the precautionary motive, when there is uncertainty in the future, the marginal utility of consumption while young will be higher; equivalently first-period consumption will be reduced, leading to more saving against those future potential contingencies. A transition to prepaid care may thus reduce the need for precautionary savings (Skinner, Reference Skinner1988), although it could at the same time create more liquidity constraints (Hubbard & Judd, Reference Hubbard and Judd1987). This effect can be quantitatively substantial as, for example, in urban China where an increase in public expenditures on healthcare led to increases in household consumption of twice the amount (Barnett & Brooks, Reference Barnett and Brooks2010).
A further potential benefit is that paying into a payroll tax while young provides a commitment mechanism to counter the tendency to continually postpone beginning a saving program that is desired, a tendency ascribed to non-constant discount rates (Samuelson, Reference Samuelson1937; Laibson, Reference Laibson1997). Poor access to banks or other saving mechanisms that make it difficult to accumulate privately for future health costs amplify the argument for public mechanisms. In this case, first-period consumption is too high, so the marginal condition is no longer equal to zero:
In this case,
![]() $\unicode[STIX]{x1D6F6}$
is the “hyperbolic” factor or the net constraint on saving that leads to inefficiency in the intertemporal allocation of consumption. Here the potential gains of moving $1 from period 1 to period 2 (in present value) through premiums, taxes, or other mechanisms by raising
$\unicode[STIX]{x1D6F6}$
is the “hyperbolic” factor or the net constraint on saving that leads to inefficiency in the intertemporal allocation of consumption. Here the potential gains of moving $1 from period 1 to period 2 (in present value) through premiums, taxes, or other mechanisms by raising
![]() $P(Y_{1})$
and reducing
$P(Y_{1})$
and reducing
![]() $P(Y_{2})$
is similar in approach to our earlier discussion of raising consumption when health is bad – in both cases, we use financing mechanisms to smooth consumption, whether across health states (as in risk reduction, above) or over time, as in this case. Thus we would use the same approach as in (4) that relies on the magnitude of
$P(Y_{2})$
is similar in approach to our earlier discussion of raising consumption when health is bad – in both cases, we use financing mechanisms to smooth consumption, whether across health states (as in risk reduction, above) or over time, as in this case. Thus we would use the same approach as in (4) that relies on the magnitude of
![]() $\unicode[STIX]{x1D6F6}$
(and hence the extent to which individuals overconsume in period 1) to estimate the gains from smoothing.Footnote
10
It is, however, more challenging to determine the true value of
$\unicode[STIX]{x1D6F6}$
(and hence the extent to which individuals overconsume in period 1) to estimate the gains from smoothing.Footnote
10
It is, however, more challenging to determine the true value of
![]() $\unicode[STIX]{x1D6F6}$
, and whether it represents a “market failure” or individual preferences, than it is to determine risks of unexpected medical expenses.
$\unicode[STIX]{x1D6F6}$
, and whether it represents a “market failure” or individual preferences, than it is to determine risks of unexpected medical expenses.
This life-cycle perspective also emphasizes that benefits and costs may vary systematically across age groups, particularly when a “pay-as-you-go” system is introduced that assesses a payroll tax on the younger working population that is used to provide benefits to an older population who had not paid into the program for many years.Footnote 11 Thus the policy analyst may also want to consider the distributional effects of an insurance expansion among age groups (Hammitt, Reference Hammitt2017), as well as across income groups (Robinson & Hammitt, Reference Robinson and Hammitt2018b ).
There are two additional factors that complicate benefit-cost evaluations of health insurance. The first is moral hazard. Because health care services are subsidized, beneficiaries may consume too much. Yet most of the literature on moral hazard suggests that individuals have a difficult time distinguishing between “high-value” and “low-value” care; higher copayments are as likely to discourage care among the sickest patients as among those less sick (Brot-Goldberg et al., Reference Brot-Goldberg, Chandra, Handel and Kolstad2017). And when there is a social welfare function of the type specified above, or even commodity egalitarianism that favors health care, we may want to minimize copayments for the poor, but perhaps not as much for the rich.
The second factor which may make cost benefit analysis of insurance more complex is the distortionary social costs of higher taxes (or deadweight cost of taxation) which could tilt the benefit-cost analysis into negative territory if distortionary taxes are used to provide health care services that higher-income households previously purchased privately (Baicker et al., Reference Baicker, Shepard and Skinner2013). When UHC involves large-scale tax reform, one requires more attention to the design of new taxes and user fees. For example, to the extent that public revenue comes from excise taxes on behavior to be discouraged (e.g. carbon and tobacco taxes) the “distortion” introduced by taxes can be partially mitigated or potentially even welfare improving.
3 Policy issues and a numerical example
What are the lessons from the literature for valuing the financial benefits of insurance expansions and universal health coverage? First, as has been well understood since Arrow (Reference Arrow1963), health insurance not only improves health, but also reduces financial risk, and any benefit-cost analysis should reflect such benefits. Indeed, in high-income countries the financial benefits of health insurance are often easier to measure than short-term health benefits (Finkelstein & McKnight, Reference Finkelstein and McKnight2008; King et al., Reference King, Gakidou, Imai, Lakin, Moore and Nall2009; Finkelstein et al., Reference Finkelstein, Taubman, Wright, Bernstein and Gruber2012). But in benefit-cost or cost-effectiveness analysis, tracing out the benefits of health insurance is not simple, as it has potentially wide-ranging effects on both prices and quantities in the health care sector, as was demonstrated by Verguet et al. (Reference Verguet, Laxminarayan and Jamison2015) in their extended CEA analysis. What should the benefit-cost analyst do in the face of all this complexity? In this section, we introduce a very simple example that shows how these financial factors could be implemented in a CBA. We note again that our example is limited only to evaluating our three risk-related and distributional factors, and not to any potential health gains, nor to potential inefficiencies arising from moral hazard or efficiency costs arising from raising taxes.
Our stylized example is shown in Table 1, with two groups, those with low incomes of $1000 in U.S. Dollars (80% of the population) and those with high incomes of $4000 (20% of the population); consumption is equal to income for the low-income group, and slightly less than income ($3800) for the high-income group. We assume an expansion of the existing insurance system that will increase per capita spending by $70, which is fully funded by an increase in premiums or tax payments of $50 for the lower-income group, and $150 by the higher-income group.
Table 1 Illustrative calculations of the financial impact of health insurance expansion.
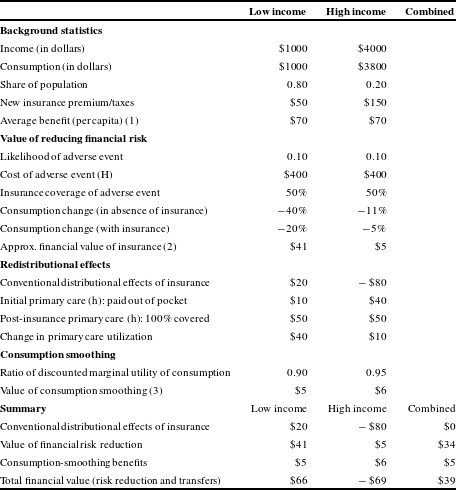
Notes: Constant relative risk aversion measure equal to 3.0. (1) Average benefit
![]() $=0.8\times 50+0.2\times 150$
. (2) For the low-income group, the value of the reduction in risk per dollar benefit is approximated by
$=0.8\times 50+0.2\times 150$
. (2) For the low-income group, the value of the reduction in risk per dollar benefit is approximated by
![]() $0.90^{\ast }(((1000/600)^{3}-1)+((1000/800)^{3}-1))/2$
. (3) For the low-income group, the smoothing gain is approximated by
$0.90^{\ast }(((1000/600)^{3}-1)+((1000/800)^{3}-1))/2$
. (3) For the low-income group, the smoothing gain is approximated by
![]() $(((1000/900)^{3}-1)+1)/2$
, multiplied by the half of the tax payment ($
$(((1000/900)^{3}-1)+1)/2$
, multiplied by the half of the tax payment ($
![]() $50/2$
) assumed paid in period 2.
$50/2$
) assumed paid in period 2.
3.1 Measuring the financial value of lower-health care risk
As noted above, we use a measure of the incremental value of reducing risk (e.g., Gertler & Gruber, Reference Gertler and Gruber2002; Chetty, Reference Chetty2006; Chetty & Looney, Reference Chetty and Looney2006) as:
where as in (4),
![]() $\unicode[STIX]{x1D703}_{j}$
depends on the degree of risk aversion, and the magnitude of the consumption decline arising from unpredictable medical expenses.
$\unicode[STIX]{x1D703}_{j}$
depends on the degree of risk aversion, and the magnitude of the consumption decline arising from unpredictable medical expenses.
One might be concerned that this measure understates the true benefit, because it is hard to assess or value financial benefits among a group of people with very little income that they can use to pay.Footnote 12 However, our approach mitigates these concerns, for at least two reasons. First, by evaluating the financial value of insurance for those in the “good” state of the world, as we do in (4 ′ ), we implicitly weight the value of financial protection for lower-income people higher than the traditional willingness to pay measures. And second, as we discuss below, it is possible to use implicit weights in a social welfare such that a given dollar benefit for lower-income household counts for more than for a higher-income household.Footnote 13
Another concern is that this equation could overstate the potential benefits because we are pricing the risk reduction for a small change, but the value of further risk reduction becomes attenuated for larger health insurance reforms with more comprehensive coverage. We address this by calculating the marginal benefit of risk reduction at the starting point, and then at the ending (post-reform) point; and then take the average of these two marginal effects.Footnote 14
For example, in Table 1 we calculate the financial benefit of the insurance program that provides 50% coverage for an adverse event (
![]() $\unicode[STIX]{x1D6F7}=0.5$
) with the probability of the adverse event (
$\unicode[STIX]{x1D6F7}=0.5$
) with the probability of the adverse event (
![]() $\unicode[STIX]{x1D70B}_{b}$
) equal to 0.10 for both high- and low-income households. Using our earlier estimate that a catastrophic event could account for as much as 40% of consumption, we use $400 as our summary approximation of the catastrophic cost, so the proposed insurance reform would reduce out-of-pocket costs from $400 to $200 for both income groups. Using the average of (4
′
), we can calculate the benefit to lower-income people as $41 (or roughly double the expected premium cost of the catastrophic component of the insurance reform), but only $5 for the higher-income households, for whom the $400 expense is a much smaller fraction of consumption.
$\unicode[STIX]{x1D70B}_{b}$
) equal to 0.10 for both high- and low-income households. Using our earlier estimate that a catastrophic event could account for as much as 40% of consumption, we use $400 as our summary approximation of the catastrophic cost, so the proposed insurance reform would reduce out-of-pocket costs from $400 to $200 for both income groups. Using the average of (4
′
), we can calculate the benefit to lower-income people as $41 (or roughly double the expected premium cost of the catastrophic component of the insurance reform), but only $5 for the higher-income households, for whom the $400 expense is a much smaller fraction of consumption.
Note also that the calculation depends on whether individuals are receiving a more generous coverage package (in which case the “copayment” rate declines), or whether more people are receiving any coverage (in which case a fraction of the population is provided with health insurance). The latter type of expansion will generate larger relief to financial risks than the former.Footnote 15
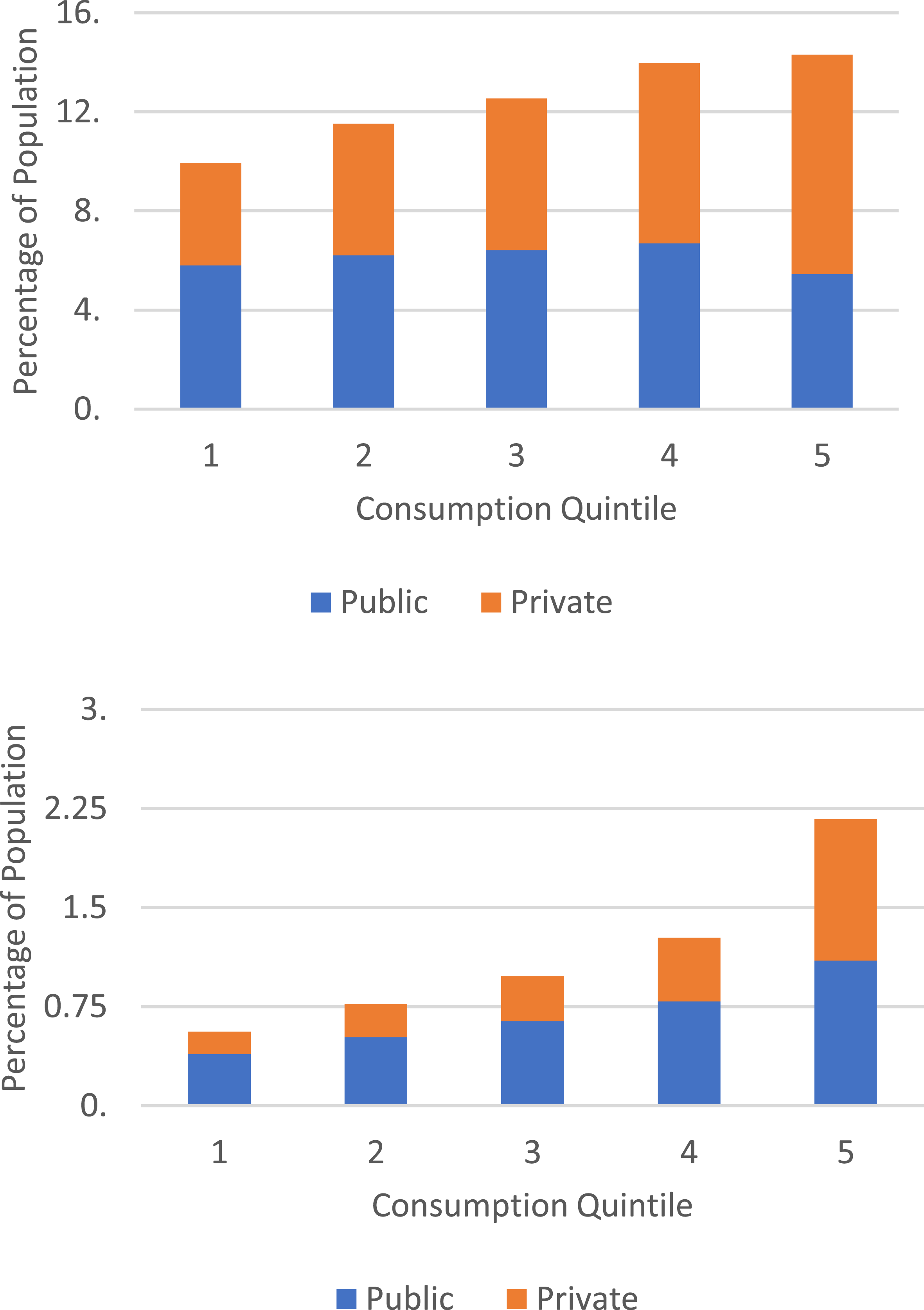
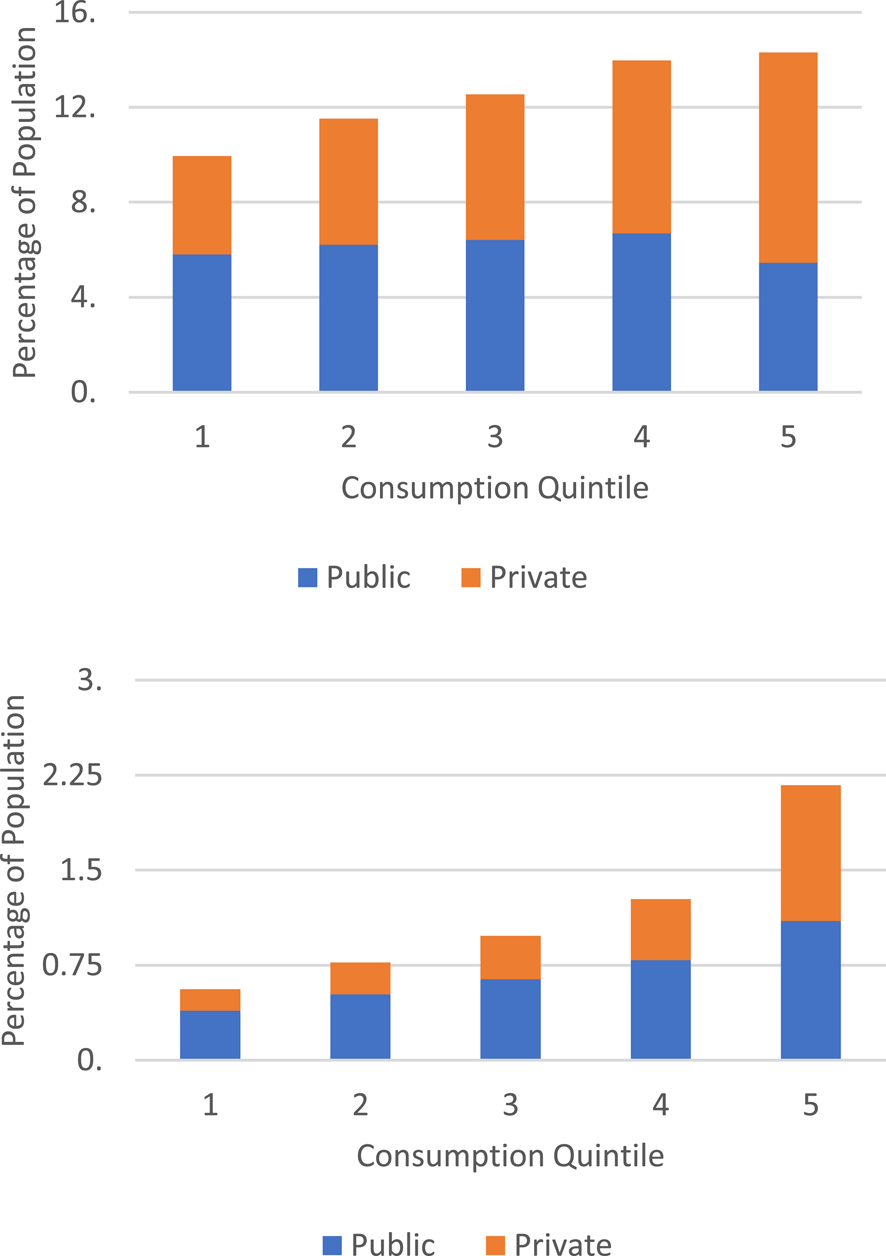
Figure 2 (a) Percentage of Population Making Clinic Visits: Indonesia, 1997. (b) Percentage of Population Making Hospital Visits: Indonesia, 1997. Sources for both Figures 2(a) and 2(b): Lanjouw et al. (Reference Lanjouw, Menno, Fadia, Haneen and Robert2002).
3.2 Estimate the incidence-based measures of expanded health insurance
There is considerable evidence in the literature that coverage and utilization is regressive rather than progressive in some countries (e.g., Castro-Leal et al., Reference Castro-Leal, Dayton, Demery and Mehra1999; Akazili et al., Reference Akazili, Welaga, Bawah, Achana and Oduro2014). One example of this can be seen in Figure 2(a) (for health clinics) and Figure 2(b) (for hospital admissions), using data from Lanjouw et al. (Reference Lanjouw, Menno, Fadia, Haneen and Robert2002) on 1997 incidence data from Indonesia. The outcome is the percentage of people who visited either a clinic (in 2(a)) or a hospital (in 2(b)) during the year. As can be seen, there is a strong upward slope with regard to consumption quintiles. (Consumption is viewed as a better way to measure ability to pay compared to income, the latter of which may fluctuate year to year); this is more pronounced with regard to private purchases, but it is positively sloped over most income levels even when considering publicly provided care in hospitals – that is, even publicly provided care is providing greater benefits to high-income compared to low-income households.Footnote 16
In Table 1, we consider the distribution impact of our hypothetical insurance reform. Under the conventional distributional measures of losers and gainers (again, without consideration of any health effects), the net gain in dollar terms would be $20 for the low-income group ($70 in benefits minus $50 in costs) and
![]() $-$
$80 for the highest income group ($70 in benefits minus $150 in costs). The catastrophic component of the plan has an expected cost of $20 per capita ($200 benefit times the 10% probability it occurs), which (for simplicity) is distributed equally to both high- and low-income households, as noted earlier. In addition, the insurance reform provides for free primary or preventive care, which we value at $50 per capita, again provided equally to high- and low-income households.Footnote
17
$-$
$80 for the highest income group ($70 in benefits minus $150 in costs). The catastrophic component of the plan has an expected cost of $20 per capita ($200 benefit times the 10% probability it occurs), which (for simplicity) is distributed equally to both high- and low-income households, as noted earlier. In addition, the insurance reform provides for free primary or preventive care, which we value at $50 per capita, again provided equally to high- and low-income households.Footnote
17
We also document the extent of “crowding out” of private by public spending.Footnote
18
As shown in Table 1, the increment in primary care spending (
![]() $h_{2}$
) is much greater for lower-income households ($40) compared to the higher-income households ($10); thus one might expect larger health benefits for the lower-income group (not included in this calculation). That said, the higher-income group also saves $40 that they would have spent on health care now that it is free, more than the $10 saved by the lower-income group.Footnote
19
$h_{2}$
) is much greater for lower-income households ($40) compared to the higher-income households ($10); thus one might expect larger health benefits for the lower-income group (not included in this calculation). That said, the higher-income group also saves $40 that they would have spent on health care now that it is free, more than the $10 saved by the lower-income group.Footnote
19
More complicated models would allow for large income and substitution effects. For example, when copayments are modest, providing insurance could encourage high-income households to expand their spending considerably compared to lower income, thus leading to even more of the subsidies flowing to higher-income households, as was found in China by Wagstaff and Lindelow (Reference Wagstaff and Lindelow2008). However, for the benefit-cost analyst working with limited data in LMICs, these perverse effects would be difficult to predict ex ante.
Another complication of accounting for distributional changes resulting from insurance expansion is that in many countries, there are multiple insurance programs for different groups of the population. For example, in Thailand, India, Jordan, and other countries, health insurance for civil servants is considerably more generous than the basic schemes for the rest. This is an example of where the transfer function of health insurance – which usually serves to equalize social resources – may work in reverse, by subsidizing higher-income employees if the frequently associated payroll taxes are insufficient to cover costs. And while the more generous benefits for civil servants could simply be schemes to raise otherwise low salaries, a full accounting of the distributional effects of one system’s insurance expansion would require understanding how the targeted expansion might affect some other potentially overlapping insurance program.
In a world where there are likely to be both winners and losers across the income distribution, how does the benefit-cost analyst determine whether the insurance expansion yields on net a social gain or loss? One seemingly simple solution is a social welfare function, which aggregates changes in well-being across high- and low-income groups, with typically greater weights for lower-income households (see Phelps et al. (Reference Phelps, Lakdawalla, Basu, Drummond, Towse and Danzon2018)). The challenge to using a social welfare function is that while we recognize the value of redistribution, there is no obvious social welfare function that will correspond to the “right” value. Instead, any tradeoffs (or range of tradeoffs) should in theory be revealed through a collective decision-making process informed by explicit social value judgments made by accountable individuals on behalf of the whole community, and that captures “extra-welfare” benefits that accrue to the community – all factors that are likely unknown to the analyst.Footnote 20 Thus we suggest caution with regard to the use of a social welfare approach, but instead recommend simply providing the net gains (or losses) by income group, where the financial net benefits could also be reported separately from any predicted health gains.
It is also worthwhile to focus explicitly on changes in the distribution of health and net income among the lowest income groups (see Asaria et al., Reference Asaria, Griffin, Cookson, Whyte and Tappenden2015). Protecting the most vulnerable from healthcare-spending-related debt (or from disease) is much less controversial than income redistribution. Providing an in-kind transfer of health care insurance, rather than simply cash, can provide additional public support (see Currie & Gahvari, Reference Currie and Gahvari2008). For these reasons, accounting separately for improved access to care across the income distribution, and among the most vulnerable, but without making explicit tradeoffs, is likely the best approach to creating a politically viable benefit-cost evaluation. A separate paper for this project (Robinson & Hammitt, Reference Robinson and Hammitt2018b ) reviews in more detail the multiple issues associated with whether and how to consider the distributional impact of health-related investments.
3.3 Measuring the benefits arising from “front-loading” insurance payments
While there is general agreement that health insurance reduces financial risk, there is less understanding of its other effects on individual and societal well-being over the life cycle. For example, health insurance funded by a payroll tax rather than age-specific premiums, as in many systems, tends to collect revenues from people years before they actually need the care. As noted in Section 2, this provides a benefit by smoothing payments over time, providing an annuity rate of return, and helping to offset the possibility of present bias and other behavioral factors that may otherwise work to discourage the purchase of private health insurance.
How does one value this “front-loading” of health insurance benefits? While we are not aware of evidence from the literature on health insurance, there is more research on the value of a social security annuity arising from payroll taxes; unfortunately, the evidence ranges too widely (e.g., Hubbard & Judd, Reference Hubbard and Judd1987; Brown et al., Reference Brown, Casey and Mitchell2007) to provide much guidance to benefit-cost analysts. Based on the previous evidence, however, biases appear to favor under-saving for future contingencies (e.g., Laibson, Reference Laibson1997), which coupled with inadequate saving mechanisms and secular increases in health care premiums, would suggest a net benefit of moving the costs of second-period health spending earlier into the life cycle when wages have risen over the life cycle, but workers are still relatively healthy. If we assume that there is an accumulated bias of 10% over an entire “period” – quite reasonable relative to typical estimates of hyperbolic discounting – for the lower-income group, and a smaller 5% gap for the high-income group, then the long-term effects of a UHC that assesses (say) half of the funding in period 1 would yield a life-cycle improvement of an additional $5 and $6, respectively, for the low- and high-income groups; the high-income group benefits slightly more in dollar terms because they are facing a larger financial burden ($150 rather than $50). Further research is needed to better understand these potential biases by income group, and indeed the design of UHC could harness those behavioral biases to encourage early participation and support (Skinner & Volpp, Reference Skinner and Volpp2017).
We sum up these three effects at the bottom of Table 1, along with the sum over both groups. As expected, the conventional societal non-health effects of a fully funded health insurance program are zero; some people pay in, while others pay out. Adding in risk reduction leads to an incremental (and societal) benefit primarily to lower-income households, while adjusting for consumption smoothing yields small benefits to each income group. In sum, our adjusted financial benefit measure yields a considerably more progressive (and higher net social gain) estimate of the non-health benefits of health insurance, with more than triple the monetary benefits to lower-income groups, and a slightly smaller decline financial for the higher-income groups.
4 Conclusion
There is considerable enthusiasm for expanding the use of health insurance to cover increasingly large fractions of the world’s populations (The Economist, 2018), but there is some confusion about how to measure the benefits arising from such expansions. Related papers address closely related issues surrounding the valuation of longevity (Robinson et al., Reference Robinson, Hammitt and O’Keeffe2019b ) and morbidity (Robinson & Hammitt, Reference Robinson and Hammitt2018a ) risk reduction, among others. In this study, we considered how best to value the financial benefits, in terms of pooling risk, intertemporal consumption smoothing, and redistribution, of expanded health insurance programs. Perhaps not surprisingly, we find that measuring insurance benefits is complicated and specific to the country setting, yet still critical to judging the value of greater insurance protection. Our objective was to provide simple and implementable approaches to assessing both risk-reduction and redistributional effects of health insurance expansion.
The financial value of a health insurance expansion depends critically on what the expansion covers, and what it does not. High-value preventive services (e.g.,
![]() $h_{2j}$
in the model above) are likely to provide larger health benefits by improving access and affordability of cost-effective primary care,Footnote
21
particularly where there are spillover effects through (e.g.) immunization services or a downstream reduction in catastrophic costs resulting from improved population health.Footnote
22
By contrast, the catastrophic coverage (
$h_{2j}$
in the model above) are likely to provide larger health benefits by improving access and affordability of cost-effective primary care,Footnote
21
particularly where there are spillover effects through (e.g.) immunization services or a downstream reduction in catastrophic costs resulting from improved population health.Footnote
22
By contrast, the catastrophic coverage (
![]() $H_{2}$
) provides, on average, deeper reductions in financial risk and the ability to buy levels of health care not previously affordable.
$H_{2}$
) provides, on average, deeper reductions in financial risk and the ability to buy levels of health care not previously affordable.
For example, some have argued against UHC because covering the smaller expenses (e.g., a visit to a clinic) could “crowd out” public or private health efforts and preclude a meaningful reduction in financial uncertainty (e.g., Hammer, Reference Hammer2015). We do not claim to resolve these difficult tradeoffs, but our model does suggest that the tradeoffs can be better understood by focusing on key country-specific parameters such as the existing coverage provided by private insurance, the incremental health benefits of expanded primary care (and the ability of the country to staff the new clinics), the costs to families of catastrophic events, potential payoffs arising from purchasing consolidation, and the estimated efficiencies from prevention and early treatment that can arise from reducing the need for expensive hospitalizations. More generally the question of how most efficiently to provide financial protection remains far less understood than the parallel question of efficiency in producing health outcomes.
In practice, some countries set up two separate funds (simultaneously or sequentially): one for catastrophic costs and one for routine more predictable and less costly (though possibly longer-term) care; Mexico is one such example. Thailand originally instituted UHC without costly interventions such as anti-retroviral treatment and dialysis included – and has now included these (Tangcharoensathien et al., Reference Tangcharoensathien and Witthayapipopsakul2018). Similarly Indonesia’s insurance program (BPJS) and India’s National Health Scheme are now including dialysis in their benefits’ packages. Other countries expand coverage for all for everything (Turkey); others exclude expensive care or leave it to development partners (e.g. Ghana’s National Health Insurance Scheme excludes HIV, tuberculosis, and malaria care). To evaluate both health-related and financial benefits of these (complex) insurance systems therefore requires country-specific information that may in practice be difficult to collect.
We have less to say about the value of having an integrated universal system, as opposed to a publicly funded safety net targeting the poorest while the wealthier sustain their private sector plans. In LMICs, the universal option often appears to deliver better outcomes at the population level; middle (and upper) classes have little interest in funding or sustaining the quality of a healthcare system from which they are excluded. The South African system is a case in point whereby less than 20% of the population absorb more than half of healthcare resources, with a significant socioeconomic and race bias (Ataguba et al., Reference Ataguba and Akazili2011). In addition to significant inequalities in access and outcomes, South Africa’s two-tier system constitutes a major obstacle to achieving the government’s vision of quality healthcare for all (Gqirana, Reference Gqirana2016). Similarly, in Peru, the experience of an approach targeting the poor have been mixed (Neelsen & O’Donnell, Reference Neelsen and O’Donnell2017). The Lancet’s Commission on Investing in Health (CIH) (Jamison et al., Reference Jamison, Summers, Alleyne, Arrow, Berkley and Binagwaho2013) concluded, however, that even in high-income countries use of out-of-pocket payments and private voluntary insurance will in all likelihood leave a substantial uninsured population. While the CIH and the global health community have come out in favor of a (hybrid) progressive universalism approach as countries transition toward UHC, the targeting vs universalism debate in social policy is ongoing (e.g., Desai, Reference Desai2017).
Although benefit-cost analysis may in some contexts influence outcomes, UHC is often determined not by maximizing a social welfare function, but through a collective decision-making process, and in fact UHC has often arisen as an election commitment device, as in Indonesia and in Turkey, as well as in high-income countries such as England where again the consensus on the National Health Service plays a critical role in elections. In this contrarian view, designing a UHC that captures political support – in part for financial protection provided – may ultimately be the deciding factor in actual implementation (Phelps et al., Reference Phelps, Lakdawalla, Basu, Drummond, Towse and Danzon2018).
There are several characteristics of health insurance that we have not addressed explicitly in this paper. For example, an additional and often neglected potential advantage of expanded coverage is that it provides much better bargaining power for enrollees seeking to reduce (e.g.) drug prices or other procurement decisions; a “countervailing power” in the sense of Galbraith (Reference Galbraith1952). This can allow for more services, lower copayments, attenuated taxes, or all three. Empirically, the ability to pool resources more effectively including when procuring commodities is a good predictor of countries’ successful “financing transition”, (Fan & Savedoff, Reference Fan and Savedoff2014) and in the ability to provide universal health coverage (UHC), this pooling is critical.Footnote 23 Whether regulated prices or so-called reference pricing can provide the same benefits is more contentious, particularly if regulated prices lead to expanded utilization and potentially higher expenditures (Prada et al., Reference Prada, Soto, Andia, Vaca, Morales, Márquez and Gaviria2018).
For medical inputs purchased from other countries, this argument is reasonable; in a LMIC setting, government officials should not care whether Pfizer earns higher or lower profits on drug sales. But when the healthcare providers are domestic, one might still want to consider how they are affected, as the health ministry’s savings could represent a reduction in nurse salaries or other payments to domestic providers. Conversely, efforts to protect a domestic pharmaceutical industry with protectionist policies would worsen budgetary pressures for the domestic health system.Footnote 24
A more challenging topic in LMICs is how to insure against the need for long-term care. The potential benefits from insuring against the enormous costs of long-term care or providing an annuity for family assistance later in life are considerable. But with higher-income people living longer, the potential for even regressive income distributional consequences are always present, as has been noted recently for the U.S. Social Security system (Isaacs & Choudhury, Reference Isaacs and Choudhury2017). For this reason, and more importantly the large and adverse budgetary implications, long-term care insurance is contentious even in many wealthy countries.
As a larger share of government budgets are devoted to providing national insurance coverage, the use of randomized trials and other types of studies will be increasingly important to ensure that the expansions deliver sufficient value given their large costs (Finkelstein et al., Reference Finkelstein, Taubman, Wright, Bernstein and Gruber2012). Identification of which specific health conditions are most responsible for financial risk, and how their impact can best be mitigated, will help guide development of health benefit packages. While this paper has attempted to lay out a basic structure for analysis to value the financial benefits of health insurance, there is a clear need for more and better empirical knowledge, both through estimation of the key parameters, and especially careful case studies. All of these advances will allow policy analysts to better quantify improvements in health, reductions in inequality, and benefits of reducing financial risk arising from the expansion of health insurance around the world.
Acknowledgments
We are grateful to Dave Greenberg, James Hammitt, Julian Jamison, Carol Levin, Erzo Luttmer, Thomas McGuire, Lisa Robinson, Saty Satyamurti, Mark Shepard, Kathy Stroffolino, two anonymous reviewers and participants at the Guidelines for Benefit-Cost Analysis Project Methods and Case Studies Workshop, November 2017 at Harvard University, for very helpful suggestions and comments. We are also grateful to the Bill & Melinda Gates Foundation for support through a grant to the Harvard T.H. Chan School, “Benefit-Cost Analysis Reference Case: Principles, Methods, and Standards” [OPP1160057], and to the National Institute on Aging (P01 AG019783). The views expressed in this paper are those of the authors and do not necessarily reflect the views of these organizations or the benefit-cost analysis project team.