Benefit–Cost Analysis of Increased Trade: An Order-of-Magnitude Estimate of the Benefit–Cost Ratio

Abstract

Drawing upon recent studies that empirically estimate both the benefits and costs of trade, this paper addresses a simple and important question: By how much do the benefits of increased global trade outweigh the costs? To the best of our knowledge, this is the first attempt to answer this question at global and World Bank income-grouping levels using empirically estimated relationships from the trade cost literature. Using a structural gravity model, we simulate changes in three primary trade constraints: a 10% reduction in tariff levels, a 10% reduction in effective distance, and a 10% increase in free trade agreement depth. The projection leads to a roughly 5% increase in global trade by value. Our model suggests that increased trade has an incredibly high benefit–cost ratio (BCR) for the developing world with an order-of-magnitude estimate for low- and lower–middle-income countries of 100 and for upper–middle-income countries of 50. However, the BCR for high-income countries is substantially lower, with a value closer to 5. Overall, the results suggest that free trade leads to substantial net benefits globally, generating US$ 700 billion in benefits (0.83% of global GDP) and US$ 100 billion in costs (0.12% of global GDP) in the first year, a differential that grows over time. Sensitivity analyses suggest that our BCRs are on the lower end of a plausible range. The results point to the incredible value of free trade, particularly for developing countries, and reiterate the importance of considering distributional impacts when implementing trade reforms.

1. Introduction

A fundamental tenet of economics is that trade between nations is beneficial for society. While there are strong theoretical reasons for this assertion, a debate on the magnitude of benefits from increased trade has existed for decades. Coinciding with a rapid increase in trade liberalization globally, substantial cross-country empirical work in the 1980s and 1990s reported positive relationships between trade openness (or trade volumes) and growth (Feder, 1983; Balassa, 1985; Esfahani, 1991; Dollar, 1992; Harrison, 1996; Frankel & Romer, 1999). These studies were critiqued as suffering several methodological shortcomings including omitted variable bias and improper controls for endogeneity (Edwards, 1993; Rodríguez & Rodrik, 2001).

More recent research across countries has attempted to address these critiques using improved identification measures such as natural experiments (Feyrer, 2021) and instrumental variable design (Feyrer, 2019). These papers have identified positive and significant income impacts from increased trade. For example, Feyrer (2019) notes that every 1% increase in trade volume generates a 0.5% increase in national income over the period 1960–1995.

While these studies have added some clarity on the net benefits from trade, another prominent body of literature puts a sharp focus on the costs of trade, particularly the effect of import competition on trade-exposed sectors of an economy. While it has long been known that opening economies to trade causes reallocation of labor (and capital), the dominant assumption had been that these reallocations were relatively swift and costless. Evidence arising out of this new body of literature, most of which has been published in the last 15 years, suggests otherwise. Labor reallocation has generated meaningful costs in terms of employment (e.g., Autor et al., 2013; Dix-Carneiro & Kovak, 2017), wages (e.g., Autor et al., 2014), and status (e.g., Autor et al., 2019) for those impacted, with effects that may persist for over a decade. This evidence provides an important context for the net benefits from trade in terms of assessing a return-on-investment from trade policy.

Considering the evidence, the purpose of this paper is to assess the simple question: By how much do the benefits of increased global trade outweigh the costs, if at all? We assess a broad order-of-magnitude benefit–cost ratio (BCR)¹ to obtain a sense of the value of increased trade in a world of limited political capital, resources, and attention. Given what we have learned about the costs of trade, does spurring more trade have a BCR closer to 2 (a fair deal), 20 (a global best buy), or 200 (one of the best of the global best buys)? To the best of our knowledge, this is the first attempt to conduct a benefit–cost analysis of increased trade at the global level that incorporates the evidence from the literature on costs borne by workers in trade-exposed industries.²

We assess this question by using a structural gravity model to simulate a 10% change in three primary trade constraints: tariff levels, effective distance, and free trade agreement depth. The simulation projects change in exports and imports at the 2-digit ISIC code level for a sample of countries that together generate more than 85% of global manufacturing trade value. Drawing from relationships estimated in the empirical literature and using multiple specifications of benefits and costs along with sensitivity analyses, a plausible range for the BCR of increased trade arising from the structural gravity simulation is identified.

To preview the results, in our preferred specification, a 10% decrease in trade constraints generates an approximate 5% increase in overall trade. Following the relationship between trade and income identified by Feyrer (2021), this leads to a persistent 0.8% increase in national income across low- and lower–middle-income countries equivalent to US$ 61 billion in the first year. Trade costs are assessed as the medium-term (15-year) losses in employment and wages for trade-exposed workers. In our model, these are estimated at the 2-digit level of the International Standard Industrial Classification of All Economic Activities (ISIC), and equal approximately US$ 1.2 billion in the first year for low- and lower–middle-income countries. This represents roughly 230,000 gross job dislocations but does not include any offsetting job gains from trade. With assumptions about the persistence of benefits and costs and adopting an 8% discount rate, the central estimate of the BCR is 95 for low- and lower–middle-income countries. Taking different specifications, an estimated range of BCRs is approximately 30 to 300. From a global perspective, annual benefits start at US$ 700 billion per year with annual costs at US$ 100 billion per year representing 2,700,000 gross job dislocations. Over the long term, the BCR of increased trade globally is 11 with range of 5–30.

There are important asymmetries in benefits and costs, both within and across countries. Low- and lower–middle-income countries experience 1% of costs and 12% of benefits, yielding a BCR of 95 (range: 31–337). High-income countries experience 91% of global costs and 57% of global benefits yielding a BCR of 7 (range: 3–18). Upper–middle-income countries face 8% of costs and receive 31% of benefits, yielding a BCR of 45 (range: 15–112). The BCRs from increased trade are 6 and 13 times larger for upper–middle-income countries and low- and lower–middle-income countries, respectively, compared to high-income countries. The difference in results between income groupings is mostly driven by the fact that countries with higher incomes have more mature manufacturing industries that are more exposed to competing imports in the structural gravity simulation.

Within countries, there is another asymmetry in benefits and costs. Benefits accrue to all individuals in the form of the increased variety of goods, lower prices, and increased national income. Costs accrue to only a sub-set of workers, predominantly manufacturing workers in trade-exposed industries and to a lesser extent, workers in sectors that may need to absorb job dislocations from manufacturing. The cost in high-income countries is equivalent to a 4 percentage point (pp) expected reduction in earnings for each trade-exposed manufacturing worker, an economically significant value.

Overall, the results suggest that efforts to increase trade represent excellent value-for-money for low- and lower–middle-income and upper–middle-income countries, with BCRs of ~100 and ~ 50, respectively. The results place freer trade as one of the top interventions across global development by BCR. However, BCRs for high-income countries and the world are closer to 5 and 10, respectively, highlighting important distributional and political considerations that must be addressed in implementing any reforms.

2. The intervention scenario

The intervention scenario is a 10% reduction in trade constraints. The focus is on three main levers: tariff levels, effective distance, and the depth of regional trade agreements (RTAs). A decrease in tariffs represents a reduction in taxes on imported goods. A decrease in the effective distance can be interpreted as innovations in transportation technology and logistics or improved transport infrastructure. An increase in the depth of RTAs is consistent with an increasing number of provisions and clauses that agreements include and the higher degree of harmonization that they imply (Dhingra et al., 2023).

To do this, we rely on the structural gravity approach. The first step is to estimate the effect of each of these factors on trade volumes. We use the gravity regression, a widely adopted approach in the international trade literature (Head & Mayer, 2014). We rely on the following empirical specification:

$$ {X}_{ij t}^k=\mathit{\exp}\left({\beta}_1^k{tariff}_{ij}^k+{\beta}_2^k{ldist}_{ij}+{\beta}_3^k{contig}_{ij}+{\beta}_4^k{lang}_{ij}+{\beta}_5^k{col}_{ij}+{\beta}_6^k{rta}_{ij}+{\gamma}_{it}^k+{\pi}_{jt}^k\right)+{\varepsilon}_{ij t}^k, $$

where indexes $ i,j,k,t $ denote exporting and importing countries, industry, and year, respectively. $ {X}_{ijt}^k $ denote trade volumes, $ {tariff}_{ij}^k $ bilateral tariffs, $ {ldist}_{ij} $ the logarithm of distance, $ {contig}_{ij} $ common border, $ {lang}_{ij} $ common language, $ {col}_{ij} $ colonial past, and $ {rta}_{ij} $ regional trade agreement dummy variables; $ {\gamma}_{it}^k $ and $ {\pi}_{jt}^k $ denote exporter-year-industry and importer-year-industry fixed effects. As recommended by Silva and Tenreyro (2006), we estimate this equation using the Poisson pseudo-maximum likelihood (PPML) technique and cluster standard errors at the exporter–importer level.

The estimates from this regression allow immediate calculation of the so-called partial equilibrium or the direct effects of counterfactual trade liberalization. Note that a corresponding counterfactual increase in trade volumes would be highly heterogeneous between different country pairs and will depend on the tariff levels and distance as well as whether both countries belong to the same RTA.

These bilateral increases in trade volumes can indirectly affect the trade of other countries by increasing the level of competition in destination markets. To address this concern, the structural gravity approach pioneered by Anderson and van Wincoop (2003) and further developed by Anderson et al. (2018) is employed. In this approach, each country’s export and import potentials are summarized by two indexes $ {\Pi}_i^k $ and $ {P}_j^k $ called multilateral resistance terms. More formally, export from country $ i $ to country $ j $ can be written as:

$$ {X}_{ij}^k=\frac{Y_i^k{E}_j^k}{Y^k}{\left(\frac{t_{ij}^k}{\Pi_i^k{P}_j^k}\right)}^{1-{\sigma}^k}, $$

where $ {Y}_i^k $ and $ {E}_j^k $ are countries $ i $ ’s and $ j $ ’s output and expenditure, $ {Y}^k $ is the world’s total output, $ {t}_{ij}^k $ are bilateral trade costs, and $ {\sigma}^k $ is the elasticity of substitution between varieties of goods imported from different countries. Note that this expression is consistent with our empirical specification. Multilateral resistance terms are then defined by the following two equations:

$$ {\Pi_i^k}^{1-{\sigma}^k}=\sum \limits_j{\left(\frac{t_{ij}^k}{P_j^k}\right)}^{1-{\sigma}^k}\frac{E_j^k}{Y^k} $$

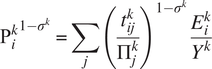$$ {{\mathrm{P}}_i^k}^{1-{\sigma}^k}=\sum \limits_j{\left(\frac{t_{ij}^k}{\Pi_j^k}\right)}^{1-{\sigma}^k}\frac{E_i^k}{Y^k} $$

Each country’s export potential is a weighted average of its destination markets’ import potentials, reflecting that it is beneficial for an exporting country to be close to large consumer markets. Similarly, each country’s import potential is a weighted sum of its’ importers’ export potentials, indicating that consumers in an importing country benefit from being close to large export markets. Heterogeneous effects of partial equilibrium trade liberalization will then lead to an adjustment of each country’s export and import potentials, which we account for. Constructing general equilibrium counterfactuals relies on the assumption on the elasticity of substitution between imported varieties $ \sigma $ . We make a standard assumption in the trade literature (e.g., Baier et al., 2019) and assume σ takes a value 4.

Previously, calculating multilateral resistance terms required solving a complex system of simultaneous equations described above; however, we rely on the most recent implementation offered by Correia et al. (2020).

3. Data

We rely on three main sources of data. The BACI (Base pour L’Analyse du Commerce International) dataset organized by Gaulier and Zignago (2010) is used. It generally relies on the UN Comtrade’s reported values but applies a special methodology that tracks for inconsistency between exporters and importers’ trade flows (trade gaps) and weights them according to the reliability of the reporting country.³ The data are available at 6-digit harmonized classification (HS) level of aggregation. We stick to the HS07 classification; therefore, the trade data are available for 2007–2019.

In the analysis, we use bilateral measures that are related to trade costs; in particular, it includes whether countries share a border, common language, and colonial past and whether they belong to the same regional trade agreement as well as the distance between each country’s most populated cities and the tariff level. All data are provided by the Centre for Prospective Studies and International Information (CEPII). Finally, the data on domestic output, wages, and employment come from the Industrial Statistics Database at 2-digit level (INDSTAT 2), with International Standard Industrial Classification of All Economic Activities (ISIC) Revision 3 classification available from the United Nations Industrial Development Organization (UNIDO). We prefer the 2-digit INDSTAT 2 database to the more disaggregated 4-digit INDSTAT 4 because the latter has much worse coverage, where data are available for only a few countries after 2015. UNIDO provides information on 19 manufacturing sectors, and we use the years 2007–2019.

We use the concordance between the HS07 and ISIC Revision 3 classification provided by the World Integrated Trade Solution to aggregate trade volumes and transition them to the UNIDO ISIC 2-digit classification. When calculating tariffs for the ISIC classification, we weight corresponding tariffs based on the relative size of the corresponding HS industry within an ISIC industry. In addition, BACI uses the ISO3 country classification, while UNIDO relies on M49 country classification; we use the concordance provided by UNSTATS and filled in the missing countries manually (Taiwan, Macao, Antilles, Sudan, Hong Kong, Romania, Serbia, Congo, and Palestine). Our general equilibrium-gravity analysis requires data on domestic production and does not allow for countries that do not export or import to at least one country. Thus, after merging the UNIDO and trade data, we drop all the trade flows corresponding to exporters or importers without information on their output in the corresponding industry. We also drop all never-exporters and never-importers for a given industry and any given year. The resulting dataset accounts for approximately 85% of the total world manufacturing trade volumes with the missing 15% due to imperfect coverage in the UNIDO data. Missing data are heavily skewed toward low- and lower–middle-income countries. We have data for only 11% of low-income countries and 67% of lower–middle-income countries by GDP. The total number of countries in the sample is 105.

4. Estimation

First, separately for each industry $ k $ , we estimate the partial equilibrium effect of all trade barriers using the PPML estimation procedure. The key estimates of interest are the effect of tariffs $ {\beta}_1^k $ , the logarithm of distance $ {\beta}_2^k $ , and RTA membership $ {\beta}_6^k $ , while the inclusion of variables for common border, common language, colonial relationship, and fixed effects $ {\gamma}_{it}^k $ and $ {\pi}_{jt}^k $ ensures that our main results are not affected by the omitted variable bias.

We then construct counterfactuals of a 10% decrease in trade costs associated with distance, tariffs, and RTA. We model it by changing the estimated effect of trade barriers, that is we decrease $ {\hat{\beta}}_1^k $ by 10%, $ {\hat{\beta}}_2^k $ by 0.046 or log(0.9) and increase the trade facilitation effect of the RTA $ {\hat{\beta}}_6^k $ by 10% (an alternative interpretation is we decrease the bilateral distance and tariffs by 10%).

We use these partial equilibrium effects of the counterfactual trade liberalization and using the methodology outlined in the previous section, calculate the corresponding general equilibrium outcomes. Global trade increases by roughly 5% due to a reduction in trade constraints by 10%. Detailed results by country of the gravity simulation are presented in the Supplementary materials.

5. Benefit–cost analysis

The benefit–cost analysis is conducted with a base year in 2023, consistent with the other papers in the Halftime Series. However, due to data availability, our gravity simulation uses 2018 as the baseline, which we assume is reasonably comparable to 2023 at least for the purposes for estimating differences in imports and exports.⁴ Figures are reported in 2020 US$. We adopt a central discount rate of 8%, following all papers in the Halftime Series and based on the recommendations of Robinson et al. (2019). In sensitivity analyses, we assess the effects of using alternative discount rates. Before describing the calculations, it is useful to briefly consider the empirical literature on the benefits and costs of trade.

6. Benefits

6.1. How does trade generate benefits?

The theoretical underpinnings for the benefits of trade can be traced back to the work of David Ricardo in the early 1800s. As noted in any undergraduate macroeconomics textbook, nations benefit through trade and exchange by specializing in the production in goods for which they have comparative advantages in the costs of production. These static welfare implications of trade have been well described and explored in numerous seminal papers and books (e.g., Bhagwati, 1971). In his Nobel Prize winning work, Krugman (1979, 1980) developed this idea further and showed that society benefits from trade due to the lower prices and greater variety of goods. These static gains are larger for larger transitions away from autarky and toward completely free trade.

Static gains from trade can be estimated relatively straightforwardly using changes in prices, demand elasticities for goods, and changes in the quantity of goods consumed. There has been extensive research studying the effect of trade on consumer prices and the variety of available goods. In their seminal paper, Arkolakis et al. (2012) showed that under certain assumptions about the demand structure, gains from trade are similar for a large class of international trade models and can be calculated with trade data and the elasticity of substitution value.

Dynamic gains, or increases in rates of income and/or income growth, are less easily estimated, and as noted in Section 1, early empirical work that attempted to estimate these gains suffered from important methodological issues. The main empirical challenge is one of endogeneity. Not only can trade lead to higher growth, but also higher growth can lead to more trade. Careful accounting of confounding factors is necessary to estimate a causal relationship between trade and growth. However, the factors that simultaneously influence trade and are unrelated to country income are difficult to isolate. A well-known “false candidate” in the trade literature is a country’s geographic factor, which was used as an instrument to estimate a trade–income relationship in Frankel and Romer (1999). However, as demonstrated by Rodríguez and Rodrik (2001), a country’s static geographic factors plausibly influence income through institutions, resource endowments, and historical experiences with colonialism. Rodríguez and Rodrik (2001) show that the inclusion of additional geographic variables (“deep determinants”) in the income equation substantially reduces the size of the coefficient on trade.

More recent work has adopted higher-quality identification strategies to address this issue. Of note for this benefit–cost analysis are the papers by Feyrer (2019, 2021), both of which used robust identification strategies to overcome confounding factors. Feyrer (2019) uses changes in air transport technology as an instrument to estimate changes in trade. Improvements in air transport technology reduce the effective air distance of trade between countries, leading to more exchange, and are plausibly exogenous to any individual country’s propensity to trade. Therefore, this can be used to predict trade or trade growth in a first-stage regression, with the resulting values used as an independent variable on income. Moreover, the use of a time series on geography allows for appropriate control of the “deep determinants” of a country’s income using country effects, thus overcoming Rodríguez & Rodrik’s (2001) critique of Frankel and Romer (1999). Using cross-country data from 1960 to 1995, the results indicate an elasticity of income per capita with respect to trade of 0.5–0.75, that is, a 10% increase in trade increases a country’s income per capita by 5–7.5%. This result holds for country-level panel data with 5-year differences, or differences over the whole-time horizon 1960–1995.

Feyrer (2021) uses the unanticipated closure of the Suez Canal between 1967 and 1975 as a natural experiment to assess the effects of trade on income. The closure and subsequent reopening generated an exogenous shock to trade distance for most countries in the world. This plausibly exogenous change in distance is used as an instrument to estimate relationships between trade and income. The results indicate an elasticity of income per capita with respect to trade of 0.15–0.25. Interestingly, these results are less than half as large as the results in Feyrer (2019). This is explained by the fact that results from the Suez Canal closure are almost exclusively related to trade, while the results from improvements in air technology relate to trade as well as other exchanges made possible by air travel, such as those involving interaction between people.

For the purposes of this study, we adopt the value of 0.2, the midpoint of the reported range in Feyrer (2021), for the elasticity of income with respect to trade. This value is chosen because it is the most plausible value that captures the effects from trade in goods. We also include the low end of the range from Feyrer (2019), 0.5 as a plausible upper bound value. We adopt these specifications assuming (1) no growth in future GDP and (2) GDP growth consistent with implied growth rates in the shared socio-economic pathways middle-of-the-road scenario (Riahi et al., 2017). Last, as a point of comparison, we include the standard measure of gains from trade common in the trade literature. These gains are calculated by the structural gravity approach along with the counterfactual trade values and reflect the approach in Arkolakis et al. (2012). As noted by Donaldson (2015), these are likely to be lower than the income impacts estimated by Feyrer (2019, 2021).

6.2. Estimation approach

For the benefit specifications based on income growth, the value of increased trade is estimated according to the following equation:

$$ Total\ benefits=\sum \limits_{t=2023}^{2023+B}\frac{\sum \limits_x\Delta \%{trade}_x\hskip0.35em \ast \hskip0.35em \theta \hskip0.35em \ast \hskip0.35em {GDP}_{t,x}}{{\left(1+r\right)}^{\left(t-2023\right)}} $$

where $ \Delta \%{trade}_x $ represents the % change in total manufacturing trade for country x, $ \theta $ is the elasticity of income with respect to trade, $ {GDP}_{t,x} $ represents national income in year t (constant 2020 US dollars) for country x, and B is the expected longevity of benefits. Given that the increase in trade is expected to remain in a steady state, the parameter B is set to 50 years. In the specifications of our benefits which assume no growth, then $ {GDP}_{t,x}={GDP}_x $ , a constant representing GDP in 2023.

7. Costs

7.1. How does trade generate costs?

Trade generates costs primarily through its impact on domestic industries that produce goods that compete with imports. Trade opens domestic workers to greater labor competition from abroad, potentially depressing wages where imports are not offset by additional exports. Moreover, where domestic firms cannot outcompete more productive international competition, they may be forced to close, leading to unemployment. These losses can be mitigated at the individual worker level by either changing jobs to more productive firms within the same industry or changing to other industries where the demand for labor is higher or has increased (e.g., due to trade opening up opportunities for exports).

However, empirical evidence indicates that worker mobility is not perfect, particularly across geographies. These frictions mean that individual workers cannot completely mitigate the losses from trade. While the overall benefits from trade may be significant in aggregate, these losses to affected workers are real and sustained. In this paper, we define the costs of trade as the consequences of workers’ imperfect abilities to adjust after changes in trade.

To calibrate parameters associated with trade costs, we conduct a literature search of studies published since 2005 that have empirically assessed the effects of trade or trade openness on worker outcomes. To keep the focus on parameters that are prima facie useful for a benefit–cost analysis, we limit the search to studies that focus mainly on worker and household economic outcomes, as opposed to social outcomes like marriage prospects or political polarization. In Section 9, we assess the potential impacts of omitted benefits and costs.

Broadly speaking, the literature can be classified into two main strands. The first group of studies examines the impact of imports from countries with comparative advantage in manufacturing (with a focus on China) on trade-exposed workers in high-income countries (see Table 1). The second group of studies examines the effects of trade liberalization episodes on various economic outcomes such as informality, wages, consumption, and poverty in low- and middle-income countries (see Table 2). In this section, we consider each group separately.

Table 1. Studies that have estimated impacts of trade on trade-exposed workers: High-income countries.

Note: Columns 5–8 represent the impact from a 1-unit change in the independent variable. References to tables do not refer to this study but those in the cited papers in column 1.

Table 2. Studies that estimate impacts of trade liberalization on worker outcomes in low- and middle-income countries. References to tables and page numbers refer to those in the cited papers in column 1.

For the high-income country studies, the most prominent event examined is the sudden increase in Chinese exports to other nations associated with the country’s increasing manufacturing productivity and accession to the World Trade Organization in the early 2000s. Some papers from this group of studies also examine the impact of imports from other countries such as former Soviet countries, other Asian countries, Mexico, and low-income countries generally. Analyses have been conducted at the levels of individual workers, firms, and local labor markets.

The independent variable of interest has typically been some measure of import exposure, from China and other countries, where import exposure is a function of imports in industries where a country has local workers. The seminal study by Autor et al. (2013), hereafter referred to as ADH, which focuses on the China Shock on U.S. manufacturing, has inspired a suite of studies adopting a similar methodology for other high-income countries. All these studies use an independent variable, measured at the local labor market level, in absolute units (typically US$ 1000) of import exposure per person of working age. Other studies have adopted different independent variables, often expressed as a percentage of import exposure or import penetration.

Table 1 presents results for some of the most commonly occurring dependent outcomes in these studies: manufacturing employment, wages, unemployment, and labor force participation (LFP). Studies adopt different specifications to measure these outcomes, which makes comparisons challenging. Even the collection of studies that explicitly follow the methodology of ADH has important yet subtle differences in variable construction, such as different currencies, currency years, and time frames for estimation of outcomes. With this caveat in mind, some broad findings stand out. Greater import exposure is always associated with reduced manufacturing employment. For studies adopting the ADH methodology, the range of impacts is roughly an order-of-magnitude spread, when the independent variable is converted to the same currency and year (Dorn & Levell, 2021).

In most cases, greater industry import exposure leads to lower wages, increased unemployment (or firm closure), and lower LFP. However, the results vary substantially based on individual country characteristics such as industry mix and employment protections. For example, in Norway, the unemployment effect is relatively large; however, the wage effect is minimal, partially reflecting strong wage protections afforded to Norwegian workers. In Germany, the results for wages and unemployment are relatively small because trade increased manufacturing in certain sectors due to greater availability of export markets (e.g., for German cars), which substantially offset losses for import-exposed industries. Moreover, not all imports had the same effects. In Australia, the impacts of Chinese imports were substantially greater than imports from other Asian nations, while in the UK and Spain, impacts were greater for Chinese imports compared to Eastern European imports.

A second group of studies examines the effects of trade liberalization episodes and trade shocks on various economic outcomes such as wages, consumption, and poverty in low- and middle-income countries. For this category, the trade variable of concern has typically been some measure of trade openness such as tariff levels, though not in all cases. These studies have been conducted in India, Mexico, Vietnam, Brazil, and Indonesia, with most of the studies examining the impact of trade liberalization in Brazil in the 1990s. Congruent with expectations, the results broadly indicate that trade policies and events that lead to greater imports reduce relative worker wages or increase relative poverty, while policies and events that lead to greater exports have the opposite effect. The results are directionally consistent with results from high-income countries. The exceptions to this are the study of trade liberalization in Mexico (Chiquiar, 2008), one of the India studies (Hasan et al., 2012) and results for overall employment but not manufacturing employment in Costa et al. (2016). For the remaining studies, there is too much heterogeneity in variable construction to conduct a comparison of impacts between studies.

Given the above exposition, what are the most appropriate parameters and variables to include in a benefit–cost analysis? Our definition of costs relates to the general equilibrium effects of increased trade. In this regard, broader measures of labor market outcomes―wages, unemployment and LFP―are likely more appropriate than manufacturing specific impacts, even though the latter has been the primary focus of many trade-cost studies. For example, if workers exit out of manufacturing to other sectors without any impact on their employability or wages (and no net general equilibrium effects to other sectors), one could plausibly argue that costs are negligible. Such an impact would be obscured by focusing on manufacturing effects only. This suggests that manufacturing level indicators and the impacts derived from studies that examine manufacturing firms only may not be appropriate.

Therefore, we adopt the mean of effect sizes noted above for unemployment, LFP, and wages as the central estimates, using results from five out of the seven studies that adopt the ADH approach (see Table 3).⁵ These studies were chosen due to similarity in methodology and variable construction that allows for some comparison between effect sizes and the generation of both point estimates and a range of potential impacts. Importantly, these impacts account for general equilibrium effects of increased trade exposure such as the reduction in wages for the services sector that absorbs former manufacturing workers. Impacts are the effect of increased trade (in exposed industries) on all workers.

Table 3. Impacts reported for earnings, unemployment and LFP, selected studies converted to 2020 US$.

Converting to 2020 US$ using currency and inflation adjustments,⁶ the effect sizes for unemployment range from 0.01 pp to 0.82 pp with a mean of 0.38 pp. For LFP, the mean effect size is 0.31 pp (range: 0.01 to 0.73). For earnings, all studies except those in the USA note minimal changes in wages. The mean is 0.09 pp.

For the purposes of conservatively estimating a BCR, we sum all costs across unemployment, LFP, and earnings, providing a maximum level of worker costs to trade. Changes in worker outcomes at the intensive margin (earnings) are added to outcomes at the extensive margin (employment and LFP) because for most of the studies in Table 1, data on earnings were only available for employed workers. Therefore, the reported impacts from previous literature, when considering earnings, do not typically account for losses in employment. Including changes to employment and LFP together probably overstates overall costs at the extensive margin because some of the workers would have left the job market anyway (e.g., through injury, retirement, etc.). However, we are not able to credibly identify how much of the losses would have incurred absent trade and so include the full amount of LFP reduction. Summing average effects, the results indicate that every 2020 US$ 1000 increase in employment-weighted industry imports per worker within a region generates a 0.78 pp (0.09 + 0.38 + 0.31 pp) reduction in gross regional earnings.⁷ To reiterate, this is the general equilibrium impact, not merely the impact on manufacturing workers.

While the studies focused on developing countries are informative and give us confidence on both the sign and external validity of the expected impacts derived from high-income countries, the differences in variable construction and outcome measurement mean that using these results is difficult for the purposes of this benefit–cost analysis. The only study that uses the same variable as ADH is Costa et al. (2016), and they find minimal or positive impacts of import exposure per worker. Therefore, for developing countries, we also adopt the impacts from the studies in Table 3.

One aspect of studies in low- and middle-income countries that is not considered in high-income countries is impacts of trade on informality. While the literature is not always consistent, the general picture emerging is that informality may act as a buffer against negative shocks arising from trade, allowing workers and firms to mitigate employment losses (Ponczek & Ulyssea, 2022). If this is the case, the cost of import shocks would be mostly reflected in wage reductions rather than increases in unemployment or labor market exit. In the sensitivity analyses, we assess an alternative specification that uses the empirical evidence on changes in informal employment from Brazil and find BCRs even higher than our main specification.

7.2. Estimation approach

Costs are estimated according to the following equation:

$$ Total\ costs=\sum \limits_{t=2023}^{2023+C}\frac{\sum \limits_x\sum \limits_i{\Delta IPW}_{ix}\hskip0.35em \ast \hskip0.35em \alpha \hskip0.35em \ast \hskip0.35em {N}_{ix}\hskip0.35em \ast \hskip0.35em {S}_{tix}}{{\left(1+r\right)}^{\left(t-2023\right)}} $$

where i denotes 2-digit industries and x denotes countries, $ {N}_{ix} $ is the baseline number of workers in industry i, in country x, and $ {S}_{tix} $ denotes their salaries in year t. The parameter, $ \alpha $ , is the sum of the average effect sizes (for earnings, unemployment, and LFP) from Table 3, and $ {\Delta IPW}_{ix} $ is the industry-country change in imports per worker derived from the gravity simulation reported in 2020 US$ 1000. The discount rate is denoted by r and C denotes the expected persistence of costs in years, over the time-period t = 2023 to t = 2023 + C. As with the benefits, some specifications include no growth and so $ {S}_{tix} $ = $ {S}_{ix} $ .

The persistence of costs is assumed to be 15 years. Autor et al. (2021) show that majority of the increase in Chinese exports as a share of global exports occurred between 2000 and 2010, plateauing thereafter. Effects persist to 2019. This suggests that in the USA, the persistence of impacts has been 10–20 years. We adopt a midpoint range of 15 years. Note this does not imply that particular individuals experience impacts for 15 years, but that the average industry level impact lasts 15 years post-import shock.

The unit of analysis for ADH and related studies is regional (i.e., a commuting zone, province, or local labor market). This was presumably done to generate sufficient sample size and meaningful variation in outcomes to run a regression. However, using these impacts in a benefit–cost analysis does not require us to adopt the same unit of analysis. As long as our subvariable i (in this case industry) collectively captures the entire labor market, the results will be the same if divided along another stratum, say regions. ⁸ We choose to conduct the cost part of the analysis at the industry level because it is arguably the most analytically logical level to project costs, and we have the data required to conduct analysis at this level. The ADH measure of import exposure uses the share of initial employment at the industry level as weights to assign the quantum of industry imports to a given region. Conducting the analysis at the industry level means that we do not have to perform this transformation, bypassing this step to reach the metric of interest: the change in imports per worker.

8. Results

Results of the analysis are presented in Table 4 for low- and lower–middle-income countries, the whole world, and other World Bank income classifications. For reporting total costs and benefits for low- and lower–middle-income countries, we first apply the estimation methodology noted above and then multiply results by a factor of $ 1/z $ , where $ z $ is the percentage of GDP in the World Bank income grouping present in the UNIDO database. This adjustment imputes missing countries as having the same costs and benefits, proportionate to GDP, as the rest of the income groupings. It does not alter the BCR but makes absolute costs and benefits somewhat more comparable to results from upper–middle-income countries and high-income countries which have full data.

Table 4. Benefit–cost analysis: Results.

Note: Standard gains from trade reflect the approach in Arkolakis et al. (2012). Remaining results depict net present values of costs and benefits under different benefit and growth specifications. The parameter, θ, denotes the elasticity of income with respect to trade volume.

Considering low- and lower–middle-income countries (the primary focus of the Halftime Series), trade generates benefits of US$ 1.4 trillion at a cost of US$ 15 billion in present value terms, using our preferred specification (column 3). In the first year, this represents a benefit of US$ 61 billion or 0.8% of GDP. Costs start at US$ 1.2 billion, representing 225,000 gross job dislocations in low- and lower–middle-income countries (124,000 leading to unemployment and 101,000 exiting the labor force). Note that this figure only includes losses associated with import competition and not any offsetting job gains from increased trade and economic activity. The BCR of increased trade is substantial at 95. Even the most conservative specification yields a BCR of 31 (column 1).

At a global level, trade generates benefits of US$ 11.8 trillion at a cost of US$ 1.0 trillion in present value terms (column 3). In the first year, this represents a benefit of US$ 701 billion or 0.87% increase in global GDP. Costs are US$ 105 billion in the first year, equivalent to 0.13% of global GDP or 3% of global manufacturing earnings. This corresponds to a global job loss of 2.7 million (1.5 million from movement into unemployment and 1.2 million from reduced LFP). The BCR of increased trade, globally, is 11.

Benefits and costs by World Bank income group provide an interesting representation of how benefits and costs are distributed across the world. High-income countries experience 92% of the costs and 57% of the benefits. The costs to high-income countries are estimated at US$ 96 billion in the first year. The total earnings of manufacturing workers in the UNIDO database are US$ 2.4 trillion. This implies that annual costs are equivalent to roughly 4% of pre-scenario earnings, most of which are experienced through job dislocations. To put this in context, the share of working age population in manufacturing in high-income countries declined by an average of 0.5% per year over the period 2010–2019 (World Bank, 2021).

Middle-income countries experience a higher share of benefits compared to costs. Upper–middle-income countries see 8% of the costs and 31% of the benefits, while for low- and lower–middle-income countries it is 1% of costs against 12% of benefits. This translates to higher BCRs for upper–middle-income countries and low- and lower–middle-income countries, 45 and 95, respectively. The primary reason why the BCRs are higher for low and lower–middle-income countries is that manufacturing industries are less mature in these countries, comprising a lower share of GDP. Moreover, manufacturing industries in low and lower–middle-income countries are less exposed to trade in our gravity simulation. For low- and lower–middle-income countries, increased trade generates lower costs, relative to the manufacturing sector and the economy overall. In our study, the costs of trade are equivalent to 0.1%, 0.6%, 0.8%, and 4.1% of pre-scenario wages in low-, lower–middle-, upper–middle- and high-income countries, respectively. Relative to pre-scenario GDP, annual costs are 0.00%, 0.02%, 0.03%, and 0.18%, respectively.

Adopting different versions of benefit specifications changes the BCRs substantially but maintains the fundamental structure: trade is modestly good for rich countries, very good for upper–middle-income countries, and amazingly good for the poorer half of the world. Using consumer surplus measures of benefits reduces central BCRs by as much as two-thirds (column 1), while using the elasticity of 0.5 from Feyrer (2019) under a growth scenario increases BCRs by as much as 300% (column 5).

8.1. Sensitivity analysis

To determine the sensitivity of results to variable and parameter choice, we conduct a series of one-way sensitivity analyses. The first set of sensitivity analyses uses the same variables and growth assumptions as in the central case but adopts variation in parameters. We vary the discount rate, length of persistence of benefits and costs, the elasticity of income with respect to trade, and the costs of trade as a function of imports per worker. Results ( Table 5) indicate that BCRs are most sensitive to the choice of elasticity of income with respect to trade, the discount rate, and magnitude of costs. However, except for the persistence of benefits assumption, all the BCR ranges in the sensitivity analysis have higher upside variation than downside relative to the central estimate. Importantly, the BCRs for upper–middle-income countries and low- and lower–middle-income countries remain high and above the BCR = 15 threshold used to assess an excellent return within the Copenhagen Consensus framework.

Table 5. Sensitivity analyses, variation in parameters.

A second set of sensitivity analyses uses different parameter specifications for benefits and costs derived from the review presented above. We present four variations:

1. 1. Costs derived from the relationship presented in Autor et al. (2014): a 1 pp increase in import penetration leads to a 6.90 pp decrease in earnings.

2. 2. Costs derived from the relationship presented in Bernard et al. (2006): a 1 pp increase in import penetration leads to a 0.515 pp reduction in employment.

3. 3. Costs derived from the relationship presented in Dix-Carneiro and Kovak (2019) for developing countries only: a 10 pp reduction in tariffs leads to a 3 pp increase in non-employment and 5.2 pp increase in informality.

4. 4. Benefits derived from Estevadeordal and Taylor (2008): a 1 pp decrease in tariff leads to a 0.22 pp increase in growth rates.

The choice of studies is motivated mostly by availability of data to implement calculations representing the reported relationships as well as using results where effect sizes were significant. For example, we choose not to demonstrate the application of the relationship presented in Dauth et al. (2014) using individual worker data because impacts are close to zero. This likely leads to a downward bias in BCRs for this part of the sensitivity analysis.

The BCRs from the first two alternative specifications generate substantially higher BCRs than the central estimates. The annual costs in the main specification start at US$ 100 billion; however, using the Autor et al. (2014) relationship yields costs of only US$ 3 billion per year. This is likely driven using only one set of costs (earnings) compared to the main specification that also includes displacement in employment. Using the Bernard et al. (2006) relationship from firm-level data reduces costs even further to US$ 200 million per year. This is implausibly low, likely because the relationship reflects costs only within manufacturing.

Adopting the result from the Brazil liberalization episode provided in Dix-Carneiro and Kovak (2019) suggests an increase in unemployment by 0.3 pp × 0.64 pp⁹ = 0.192 pp and an increase in informality of 0.52 pp × 0.64 pp = 0.33 pp. Further, we assume that informal earnings are 25% of formal earnings (McCaig & Pavcnik, 2018). The per-worker costs of trade (assessed at 100% of pre-scenario wages) and informality (assessed at 25% of pre-scenario wages) are therefore 0.192 + 0.33 × 25% = 0.28% of pre-scenario wages. This cost is lower than the costs of the ADH approach, meaning that BCRs are higher if using the relationship in Dix-Carneiro and Kovak (2019). If applied to developing countries only, this approach yields a BCR of 223 for low- and lower–middle-income countries, 127 for upper–middle-income countries, and 12 for the world.

The working paper by Estevadeordal and Taylor (2008) represents a potential improvement over early research efforts identifying the relationship between trade and income insofar as they adopt a difference-in-difference estimation methodology. However, they do not test parallel trends in treatment and control groups, a central assumption for difference-in-difference estimation. It is likely that liberalizers and nonliberalizers in their sample differ in important ways such that, even in the absence of opening to trade, trends in income would not be parallel. Nevertheless, we adopt their approach to demonstrate the application of changes in rates of income growth rather than levels, as in the base case. The 0.64 pp tariff reduction from our model translates to an increase in growth rates of 0.64 × 0.22 = 0.14 pp. Using this alternative, benefits specification increases BCRs by roughly 300%, mainly due to compounding growth gains that are absent in our main specification. For low- and lower–middle-income countries, the BCR is 325 while for the world it is 31.

These results suggest that our choice of variables in the main specification is not biased in favor of those that would lead to a high BCR. If anything, the sensitivity analysis demonstrates that our choice of variables and the parameters used for those variables are on the conservative side.

9. Discussion

This benefit–cost analysis shows that the net benefits from increased trade are substantial. At a global level, a 10% reduction in trade constraints would yield an estimated US$ 700 billion in benefits initially while costs would be in the order of US$ 100 billion in the first year. Over a time horizon of 50 years, and assuming transition costs last 15 years, the net benefits of the intervention are US$ 17.7 trillion with a BCR of 11. The returns for developing countries are even greater. Upper–middle-income countries and low- and lower–middle-income countries experience BCRs of 45 and 95, respectively, making trade one of the highest returning interventions in global development.

There are several ways in which the results of the analysis potentially deliver conservative BCRs. First, the main cost parameters are taken from ADH and related studies that examined the impact of Chinese imports on workers across high-income countries. We take the effect size from Chinese imports and apply this to all imports simulated in the structural gravity analysis regardless of origin. However, in many of the China Shock studies, the impact of imports from other regions (such as Eastern Europe and Asia) yielded limited effects. If the impacts from Chinese imports are representative of the upper bound of effect sizes, using those impacts would generate higher costs and lower BCRs.

Second, the impacts noted in the China Shock studies are relative effects, comparing regions with higher exposure to imports relative to regions with less exposure to imports. In this analysis, we treat the effect sizes as absolute effects, which we believe is reasonable given the relatively small average per capita income gains from trade (2% per year) and the average earnings losses experienced by trade-exposed workers (4% per year). However, these average effects would be distributed unevenly across individuals and regions. Imagine if there are some cases where baseline conditions would lead to an overall income increase of 2%, while increased trade yields substantial broad absolute gains for all (e.g., 8%), but with trade-exposed workers experience fractionally lesser gains (e.g., 6%). These trade-exposed workers would clearly experience a 2% lower gain, but it is unclear whether it is right to say it is a 2% loss when, in fact, they still gained 4% more compared to the no-trade increase scenario. To the extent that this occurs, our BCRs might overstate costs.

Third, impacts derived from Feyrer (2019, 2021) represent a net benefit measure. This arises from the methodological specification where GDP is the dependent variable, which reflects the net effect from sectoral expansions and contractions associated with trade. In this analysis, we treat the Feyrer impacts as gross gains. Technically, we should also add the costs to the net benefits to estimate the gross benefits and use that value in the numerator of the BCR. We choose not to do this for the sake of parsimony and conservatism. This adjustment would only increase BCRs by 1, leaving our conclusions unchanged.

The analysis includes some notable limitations. Our estimates of costs and benefits did not include second-order effects. However, it is unclear whether these second-order effects would raise or lower the BCR. Consider the second-order effects around marriage and fertility. Autor et al. (2021) document that greater trade exposure reduced marriage and fertility for men while increasing premature mortality in the USA. Including these would increase costs and reduce the BCR. At the same time, Heath and Mobarak (2015) note that the presence of ready-made-garment factories in Bangladesh (most of which serve export markets) increased female educational attainment, reduced child marriage, and delayed fertility, all important benefits in the context of a developing nation. Moreover, given the links between fertility reduction and future demographic dividends in high fertility environments (Ashraf et al., 2013), these impacts may generate even further benefits. Understanding the relative magnitude of these second-order effects globally is left for future research.

Another limitation of our analysis is that we do not include costs or benefits of increased agricultural trade. We do this because the studies from which we adopt parameters focus on impacts to manufacturing industries. This is unlikely to affect our broad conclusions. Agricultural trade by value is less than 7% of total global trade in goods. The FAO estimates that in 2020, agricultural trade totaled US$ 1.5 trillion (FAO, 2022). This compares to total trade in goods of roughly US$ 23 trillion in the same year (UNCTAD, 2022). The magnitude of costs, benefits, and BCRs are unlikely impacted by the exclusion of agricultural trade.

One might argue that the exclusion of agriculture could impact the relative BCRs between high-income and low- and lower–middle-income countries, since a larger share of labor in the developing world is employed in agriculture. However, there are sound reasons for why the direct impacts would be materially different for agricultural workers compared to manufacturing workers. One important difference is that those working in manufacturing are typically employees of a company, while those working in agriculture are self-employed (micro-) entrepreneurs. Those who have their employability impacted in manufacturing are more subject to the labor opportunities available in the market. They typically cannot start their own manufacturing enterprise to mitigate losses and take advantage of shifts in the prospects of different manufacturing industries. Farmers, particularly those in developing countries, both by necessity and by the greater flexibility of their work, can more readily shift production into different commodities if imports diminish the viability of a given crop. While this is not likely to be costless, it is also unlikely to have the same multiyear persistent effects as documented in manufacturing.

In summary, while the benefits of more trade are substantial, the costs are real and substantial. Our benefit–cost analysis of a 10% reduction in trade constraints predicts 2,700,000 gross job dislocations globally, with 92% of the costs incurred in high-income countries. These losses are estimated at US$ 100 billion per year initially, but they are a tenth of the expected benefits from increased trade globally. Moreover, the net present value of benefits is equal to US$ 4.4 million per job dislocation. The BCRs in developing countries are even larger, making trade a “best buy” in global development. The results point to the need to carefully consider the distributional effects of increased trade when planning reforms.