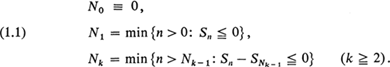Use is often made of the Wiener and Ornstein-Uhlenbeck (O.U.) processes in various applications of stochastic processes to problems of engineering interest. These applications frequently involve the presence of barriers. Although mathematical methods for solving Kolmogorov's forward equation for the above processes have previously been discussed ([1], [2]), many solutions for problems with two barriers do not seem to be available in the literature. Instead, one finds solutions for unrestricted processes or simulation used in place of analytical solutions in various applications ([3], [4], [5]). In this paper, solutions of Kolmogorov's forward equations in the presence of constant absorbing and/or reflecting barriers are obtained by means of separation of variables. This enables one to obtain expressions for the probability density functions for first passage times when absorbing barriers are present. The solution for the O.U. process is used to obtain a result of Breiman's [6] concerning first passage times.

Let X(t), t ≧ 0, be a stationary Gaussian process with zero mean, unit variance and continuous covariance function r(t). Suppose that, for some ε > 0 so that there is a version of the process whose sample functions are continuous [1].

Suppose F is a one-dimensional distribution function, that is, a function from the real line to the real line that is right-continuous and non-decreasing. For any such function F we shall write F{I} = F(b)– F(a) where I is the half-open interval (a, b]. Denote the k-fold convolution of F with itself by Fk* and let Now if z is a non-negative function we may form the convolution although Z may be infinite for some (and possibly all) points.

In the type II counter with constant deadtime, particles which arrive within some constant time τ following another particle are unrecorded. We can think of this process as an alternating sequence of gaps and bunches of events. Gaps have duration > τ, while the intervals between any successive pair of events within a bunch are all ≦ τ. Counter theory is usually concerned with the distribution of intervals between recorded events (i.e., the first event of each bunch) and the distribution of the number of recorded events in a given time interval. In the case where the events form a renewal process this has been studied intensively by Pyke [2], Smith [5] and Takács [6].

Let X1, X2, X3, ··· be independent, identically distributed random variables on a probability space (Ω, F, P); and with a continuous distribution function. Let the sequence of indices {Vr} be defined as Also define The following theorem is due to Renyi [5].

The concept of cost has not, until recently, been investigated in any detail within the framework of epidemic theory. In the case of minor illnesses a pertinent estimate of cost may be the man-hours lost in industry during an outbreak. For the general epidemic, in which the removals are immune recoveries (or deaths), this is conveniently represented by the area generated by the trajectory in time t of infectives I(t) until the epidemic ceases. A small element of area under the trajectory is I(t)δt and represents I(t) infectives withdrawn from the labour force for a small time δt; the total work-time lost is thus represented by where T is the duration of the epidemic.

Let be a sequence of non-negative random variables and the associated point process defined by

We consider the point process i + τi (i = 0, ± 1, ± 2, . . .), where the τi(assumed for convenience to be positive) are independent random samples from the same distribution. We define an inter-arrival interval as the stretch between neighbouring events, which need not belong to successive values of i, because of the jumbling of position occasioned by the variability of the τ. We obtain explicit expressions for the distribution of inter-arrival intervals in general, as well as the correlation coefficient between successive inter-arrival intervals in the case where the τ are exponentially distributed.

The queueing system with alternating priorities has been discussed recently in numerous articles (Maxwell [1], Avi Itzhak, Maxwell, Miller [2], Neuts, Yadin [3], and others). Consider a system which consists of several queueing units. Each unit is independent in the sense that it has its own waiting line which is generated by an independent Poisson stream of customers. However, all of the units are served by a single server who allocates his time between the units.

Denote by SN,r the set of r-tuples n having non-negative integer components summing to N, and by ei the r-tuple having a one in the ith position and zeros elsewhere. For m and n belonging to SN r, we let P(n, t|m, s) represent the transition probability of moving from state m at time s to state n at time t. Bartlett's conservative process [1] assumes that for n–ei + ej and n ∈ SN,r and Δt > 0 where the λij(t) are non-negative continuous functions of t.

Gnedenko's classical work [1] on the limit of the distribution of the maximum of a sequence of independent random variables is extended to the distribution of the maximum of a sequence of random variables defined on a finite Markov chain.

We consider a population which evolves at discrete points in time by branching and immigration, and in which each member reproduces independently of all others. Let Fn(x) denote the probability generating function (P.G.F.) of the number of offspring produced by each member of the nth generation, Bn–1(x) the P.G.F. of the number of immigrants joining the nth generation and Zn the population size in the nth generation. We write

In this paper it is shown that the distribution of the instant of service of a customer is symmetric as between the distributions of service and interarrival time. Also U(t), the expected number of departures in (0, t), is a delayed renewal function for the GI/M/1 queue.

Assume the sequence of random variables x0, x1, x2, ··· forms a two-state, homogeneous Markov chain with transition probabilities and initial probabilities

We consider a single server queueing system with inter-arrival times {un, n ≧ 1}, and service times {υn, n ≧ 1} and the queue-discipline, ‘first-come, first-served’. It is assumed that {un} and {υn} are two independent renewal processes, and 0 > E(un) =a < ∞, 0 < E(υn) = b < ∞. The traffic intensity is P ρ b/a(0 > ρ > ∞). This paper is concerned with the case ρ = 1, where it is known that the various queueing processes such as the queue-length Q(t) and waiting time W(t) diverge to + ∞ in distribution as t → ∞. Borovkov [1], [2] and Brody [3] have obtained limit distributions for Q(t) and W(t) with appropriate location and scale parameters in the cases P ≧ 1. Here we investigate random variables related to the busy and idle periods in the system. To explain our approach, we consider the random variables Xn = υn – un (n ≧ 1). Let S0 ≡ 0, Sn = X1 + X2 + ··· + Xn (n ≧ 1), and define the sequence {Nk, k ≧ 0} as

Let Z0 = 1, Z1, Z2, ··· denote a super-critical Galton-Watson process whose non-degenerate offspring distribution has probability generating function where 1 < m = EZ1 < ∞. The Galton-Watson process evolves in such a way that the generating function Fn(s) of Znis the nth functional iterate of F(s). The convergence problem for Zn, when appropriately normed, has been studied by quite a number of authors; for an ultimate form see Heyde [2]. However, no information has previously been obtained on the rate of such convergence. We shall here suppose that in which case Wn = m –nZn converges almost surely to a non-degenerate random variable W as n → ∞ (Harris [1], p. 13). It is our object to establish the following result on the rate of convergence of Wn to W.

We consider a stochastic process which increases and decreases by simple jumps as well as smoothly. The rate of smooth increase and decrease with time is a function of the state of the process. The process is not constant in time except when in the zero state. For such processes a relation is derived between the expected number of true crossings (as opposed to skippings by which we mean vertical crossings due to jumps) of a level x, say, and the time dependent distribution of the process. This result is applied to the virtual waiting time process of the GI/G/1 queue, where it is of particular interest when the zero level is considered, as the underlying crossing process is then a renewal process. It leads to a new derivation of the busy period distribution for this system. This serves as an example for the last brief section, where an indication is given as to how this method may be applied to the GI/G/s queue. Naturally, the present method is most powerful when the original process is a Markov process, so that renewal processes are imbedded at all levels. For an application to the M/G/1 queue, see Roes [3].

This note describes a model for inflow-stock-outflow time series which are formed as sums of random numbers of subcomponents of randomly determined sizes and are related via a probabilisticly distributed lag. Such time series may be illustrated by population processes in connection with which not only numbers of units are of interest but also the sizes of the units and the sums of the sizes. Such series may also be illustrated by economic phenomena like new loans made, loans outstanding and loans repaid of a commercial bank; new capital investments, capital stock and depreciated capital for a group of firms as well as accessions to the labor force, labor force outstanding, and secessions from the labor force.

Let {Xk}, k = 1, 2, ··· be a sequence of random variables forming a homogeneous Markov chain on a finite state-space, S = {1, 2, ···, s}. Xk could be thought of as the state at time k of some physical system for which are the (one-step) transition probabilities. It is assumed that all the states are inter-communicating, so that the transition matrix P = ((pij)) is irreducible.

Let Zn be the number of descendents in the nth generation of a simple Galton-Watson branching process, initiated by a single progenitor, Z0 = 1. If E(Z1) < ∞ the limiting distribution of Zn is known in some detail, and a comprehensive account is given in Seneta [1]. If E{Z1) = ∞ (the “explosive” case) the behavior of the distribution of Zn for large n seems not to be known. As shown by Seneta [1], there are no constants cn such that cnZn has a non-degenerate limiting distribution but it turns out that, under conditions given below, log(Zn + 1) has a limiting distribution.