Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T07:13:59.456Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit theorems for the single server queue with traffic intensity one

Published online by Cambridge University Press:  14 July 2016

N. U. Prabhu
N. U. Prabhu*
Affiliation:
Cornell University
Get access Rights & Permissions [Opens in a new window]

Extract

We consider a single server queueing system with inter-arrival times {un, n ≧ 1}, and service times {υn, n ≧ 1} and the queue-discipline, ‘first-come, first-served’. It is assumed that {un} and {υn} are two independent renewal processes, and 0 > E(un) =a < ∞, 0 < E(υn) = b < ∞. The traffic intensity is P ρ b/a(0 > ρ > ∞). This paper is concerned with the case ρ = 1, where it is known that the various queueing processes such as the queue-length Q(t) and waiting time W(t) diverge to + ∞ in distribution as t → ∞. Borovkov [1], [2] and Brody [3] have obtained limit distributions for Q(t) and W(t) with appropriate location and scale parameters in the cases P ≧ 1. Here we investigate random variables related to the busy and idle periods in the system. To explain our approach, we consider the random variables Xn = υn – un (n ≧ 1). Let S0 ≡ 0, Sn = X1 + X2 + ··· + Xn (n ≧ 1), and define the sequence {Nk, k ≧ 0} as

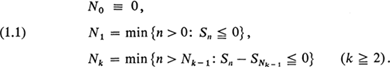
Type
Research Papers
Information
Journal of Applied Probability , Volume 7 , Issue 1 , April 1970 , pp. 227 - 233
Copyright
Copyright © Applied Probability Trust 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Borovkov, S. P. (1964) Some limit theorems in the theory of mass service, I. Theor. Probability Appl. 9, 550–565. (English Translation).Google Scholar
[2] Borovkov, S. P. (1965) Some limit theorems in the theory of mass service, II. Theor. Probability Appl. 10, 375–400. (English Translation).Google Scholar
[3] Brody, S. M. (1963) On a limit theorem of the theory of queues. Ukrain Mat. Z. 15, 76–79.Google Scholar
[4] Darling, D. A. and Kac, M. (1957) On the occupation times for Markov processes. Trans. Amer. Math. Soc. 84, 444–458.CrossRefGoogle Scholar
[5] ErdöS, P. and Kac, M. (1946) On certain limit theorems of the theory of probability. Bull. Amer. Math. Soc. 52, 292–302.Google Scholar
[6] Feller, W. (1966) An Introduction to Probability Theory and its Applications, Vol. II. John Wiley, New York.Google Scholar
[7] Heyde, C. C. (1967) A limit theorem for random walks with drift. J. Appl. Prob. 4, 144–150.Google Scholar
[8] Iglehart, D. L. (1965) Limit theorems for queues with traffic intensity one. Ann. Math. Statist. 36, 1437–1449.Google Scholar
[9] Kendall, D. G. (1957) Some problems in the theory of dams. J. R. Statist. Soc. B19, 207–212.Google Scholar
[10] Prabhu, N. U. (1968) Some new results in storage theory. J. Appl. Prob. 5, 452–460.Google Scholar
[11] Prabhu, N. U. (1969) The queue G//M/1 with traffic intensity one (to appear).Google Scholar
[12] Sinai, Y. G. (1957) On the distribution of the first positive partial sum for a sequence of independent random variables. Theor. Probability Appl. 2, 122–129. (English translation).Google Scholar
[13] Whitt, W. (1968) Weak Convergence Theorems for Queues in Heavy Traffic. Ph. D. Thesis, Cornell University.Google Scholar