Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tweedie, Richard L.
1973.
The calculation of limit probabilities for denumerable Markov processes from infinitesimal properties.
Journal of Applied Probability,
Vol. 10,
Issue. 01,
p.
84.
Tweedie, Richard L.
1975.
Truncation approximation of the limit probabilities for denumerable semi-Markov processes.
Journal of Applied Probability,
Vol. 12,
Issue. 01,
p.
161.
Tweedie, Richard L.
1975.
Truncation approximation of the limit probabilities for denumerable semi-Markov processes.
Journal of Applied Probability,
Vol. 12,
Issue. 1,
p.
161.
Wolf, D.
1980.
Approximation of the invariant probability measure of an infinite stochastic matrix.
Advances in Applied Probability,
Vol. 12,
Issue. 3,
p.
710.
Wolf, D.
1980.
Approximation of the invariant probability measure of an infinite stochastic matrix.
Advances in Applied Probability,
Vol. 12,
Issue. 3,
p.
710.
Zijm, W. H. M.
1983.
R-theory for countable reducible nonnegative matrices.
Stochastics,
Vol. 10,
Issue. 3-4,
p.
243.
Tweedie, R. L.
1986.
The Craft of Probabilistic Modelling.
Vol. 1,
Issue. ,
p.
291.
Tweedie, R. L.
1998.
Truncation approximations of invariant measures for Markov chains.
Journal of Applied Probability,
Vol. 35,
Issue. 03,
p.
517.
Dunsmuir, William T. M.
Meyn, Sean P.
and
Roberts, Gareth
2002.
Obituary: Richard Lewis Tweedie.
Journal of Applied Probability,
Vol. 39,
Issue. 2,
p.
441.
Dunsmuir, William T. M.
Meyn, Sean P.
and
Roberts, Gareth
2002.
Obituary: Richard Lewis Tweedie.
Journal of Applied Probability,
Vol. 39,
Issue. 2,
p.
441.
Hart, Andrew G.
and
Tweedie, Richard L.
2012.
Convergence of Invariant Measures of Truncation Approximations to Markov Processes.
Applied Mathematics,
Vol. 03,
Issue. 12,
p.
2205.
van Doorn, Erik A.
and
Pollett, Philip K.
2013.
Quasi-stationary distributions for discrete-state models.
European Journal of Operational Research,
Vol. 230,
Issue. 1,
p.
1.
Baumann, Hendrik
2020.
Finite-State-Space Truncations for Infinite Quasi-Birth-Death Processes.
Journal of Applied Mathematics,
Vol. 2020,
Issue. ,
p.
1.
Randone, Francesca
Bortolussi, Luca
and
Tribastone, Mirco
2021.
Refining Mean-field Approximations by Dynamic State Truncation.
p.
31.
Randone, Francesca
Bortolussi, Luca
and
Tribastone, Mirco
2021.
Refining Mean-field Approximations by Dynamic State Truncation.
Proceedings of the ACM on Measurement and Analysis of Computing Systems,
Vol. 5,
Issue. 2,
p.
1.
Randone, Francesca
Bortolussi, Luca
and
Tribastone, Mirco
2021.
Refining Mean-field Approximations by Dynamic State Truncation.
ACM SIGMETRICS Performance Evaluation Review,
Vol. 49,
Issue. 1,
p.
31.
Kuntz, Juan
Thomas, Philipp
Stan, Guy-Bart
and
Barahona, Mauricio
2021.
Stationary Distributions of Continuous-Time Markov Chains: A Review of Theory and Truncation-Based Approximations.
SIAM Review,
Vol. 63,
Issue. 1,
p.
3.


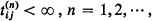 where
where  are the matrix iterates of
are the matrix iterates of 