Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Chihara, Theodore S.
and
Ismail, Mourad E.H.
1982.
Orthogonal polynomials suggested by a queueing model.
Advances in Applied Mathematics,
Vol. 3,
Issue. 4,
p.
441.
Conolly, B. W.
1983.
More transient results for generalised state-dependent Erlangian queues.
Advances in Applied Probability,
Vol. 15,
Issue. 3,
p.
688.
Ismail, Mourad E.H
1985.
A queueing model and a set of orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 108,
Issue. 2,
p.
575.
Montazer-Haghighi, A.
Medhi, J.
and
Mohanty, S.G.
1986.
On a multiserver markovian queueing system with balking and reneging.
Computers & Operations Research,
Vol. 13,
Issue. 4,
p.
421.
Chihara, Laura M
and
Chihara, T.S
1987.
A class of nonsymmetric orthogonal polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 126,
Issue. 1,
p.
275.
Zeifman, A. I.
1991.
Some estimates of the rate of convergence for birth and death processes.
Journal of Applied Probability,
Vol. 28,
Issue. 2,
p.
268.
Zeifman, A. I.
1991.
Qualitative properties of inhomogeneous birth and death processes.
Journal of Soviet Mathematics,
Vol. 57,
Issue. 4,
p.
3217.
Browne, Sid
and
Sigman, Karl
1992.
Work-modulated queues with applications to storage processes.
Journal of Applied Probability,
Vol. 29,
Issue. 03,
p.
699.
Sharma, O.P.
and
Maheswar, M.V.R.
1993.
Transient behaviour of a simple queue with discouraged arrivals.
Optimization,
Vol. 27,
Issue. 3,
p.
283.
Granovsky, B. L.
and
Zeifman, A. I.
2000.
Nonstationary Markovian queues.
Journal of Mathematical Sciences,
Vol. 99,
Issue. 4,
p.
1415.
Coolen-Schrijner, Pauline
and
Van Doorn, Erik A.
2001.
On the convergence to stationarity of birth-death processes.
Journal of Applied Probability,
Vol. 38,
Issue. 3,
p.
696.
Askey, R.
Ismail, M.E.H.
and
Van Assche, W.
2001.
Ted Chihara and his work on orthogonal polynomials.
Journal of Computational and Applied Mathematics,
Vol. 133,
Issue. 1-2,
p.
1.
Coolen-Schrijner, Pauline
and
Van Doorn, Erik A.
2001.
On the convergence to stationarity of birth-death processes.
Journal of Applied Probability,
Vol. 38,
Issue. 03,
p.
696.
2004.
Birth and Death (BDP) Process Models with Applications.
American Journal of Mathematical and Management Sciences,
Vol. 24,
Issue. 1-2,
p.
1.
Zeifman, A. I.
and
Satin, Ya. A.
2007.
Mean characteristics of Markov queueing systems.
Automation and Remote Control,
Vol. 68,
Issue. 9,
p.
1583.
Белорусов, Тимофей Николаевич
and
Belorusov, Timophey Nikolaevich
2011.
Эргодичность многоканальной системы обслуживания с возможностью неприсоединения к очереди.
Теория вероятностей и ее применения,
Vol. 56,
Issue. 1,
p.
145.
Belorusov, T. N.
2012.
Ergodicity of a Multichannel Queueing System with Balking.
Theory of Probability & Its Applications,
Vol. 56,
Issue. 1,
p.
120.
Ammar, S. I.
El-Sherbiny, A. A.
El-Shehawy, S. A.
and
Al-Seedy, R. O.
2012.
A matrix approach for the transient solution of an M/M/1/N queue with discouraged arrivals and reneging.
International Journal of Computer Mathematics,
Vol. 89,
Issue. 4,
p.
482.
Abdul Rasheed, K. V.
and
Manoharan, M.
2016.
Markovian Queueing System with Discouraged Arrivals and Self-Regulatory Servers.
Advances in Operations Research,
Vol. 2016,
Issue. ,
p.
1.
Satin, Yacov
Zeifman, Alexander
Sipin, Alexander
Ammar, Sherif I.
and
Sztrik, Janos
2020.
On Probability Characteristics for a Class of Queueing Models with Impatient Customers.
Mathematics,
Vol. 8,
Issue. 4,
p.
594.


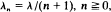 and
and 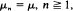 which serves as a queueing model where potential customers are discouraged by queue length.
which serves as a queueing model where potential customers are discouraged by queue length.