Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T00:45:16.605Z Has data issue: false hasContentIssue false
  • English
  • Français

A temporal factorization at the maximum for certain positive self-similar Markov processes

Part of: Stochastic processes

Published online by Cambridge University Press:  23 November 2020

Matija Vidmar
Matija Vidmar*
Affiliation:
University of Ljubljana
*
*Postal address: Department of Mathematics, Faculty of Mathematics and Physics, University of Ljubljana, Jadranska ulica 21, 1000 Ljubljana, Slovenia. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a spectrally negative self-similar Markov process on 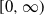$[0,\infty)$ with an a.s. finite overall supremum, we provide, in tractable detail, a kind of conditional Wiener–Hopf factorization at the maximum of the absorption time at zero, the conditioning being on the overall supremum and the jump at the overall supremum. In a companion result the Laplace transform of this absorption time (on the event that the process does not go above a given level) is identified under no other assumptions (such as the process admitting a recurrent extension and/or hitting zero continuously), generalizing some existing results in the literature.

Keywords

spectrally negative Lévy processespositive self-similar Markov processessplitting at the maximumWiener–Hopf factorizationmartingalestime-changes

MSC classification

Primary: 60G51: Processes with independent increments; L'evy processes 60G18: Self-similar processes
Secondary: 60G44: Martingales with continuous parameter
Type
Research Papers
Information
Journal of Applied Probability , Volume 57 , Issue 4 , December 2020 , pp. 1045 - 1069
Check for updates
Copyright
© Applied Probability Trust 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avram, F., Kyprianou, A. E. and Pistorius, M. R. (2004). Exit problems for spectrally negative Lévy processes and applications to (Canadized) Russian options. Ann. Appl. Prob. 14, 215–238.Google Scholar
Barczy, M. and Döring, L. (2013). On entire moments of self-similar Markov processes. Stoch. Anal. Appl. 31, 191–198.10.1080/07362994.2013.741397CrossRefGoogle Scholar
Bertoin, J. (1996). Lévy Processes (Camb. Tracts Math.). Cambridge University Press.Google Scholar
Bertoin, J. and Yor, M. (2002). On the entire moments of self-similar Markov processes and exponential functionals of Lévy processes. Ann. Fac. Sci. Toulouse Math. (6) 11, 33–45.10.5802/afst.1016CrossRefGoogle Scholar
Blumenthal, R. M. (2012). Excursions of Markov Processes (Probability and Its Applications). Birkhäuser, Boston.Google Scholar
Chaumont, L. and Doney, R. (2005). On Lévy processes conditioned to stay positive. Electron. J. Prob. 10, 948–961.10.1214/EJP.v10-261CrossRefGoogle Scholar
Chaumont, L., Kyprianou, A., Pardo, J. C. and Rivero, V. (2012). Fluctuation theory and exit systems for positive self-similar Markov processes. Ann. Prob. 40, 245–279.10.1214/10-AOP612CrossRefGoogle Scholar
Doney, R. A. (2007). Fluctuation Theory for Lévy Processes: Ecole d’Eté de Probabilités de Saint-Flour XXXV – 2005. (Lecture Notes Math. 1897). Springer, Berlin and Heidelberg.Google Scholar
Getoor, R. K. and Blumenthal, R. M. (2011). Markov Processes and Potential Theory. Academic Press.Google Scholar
Greenwood, P. and Pitman, J. (1980). Fluctuation identities for Lévy processes and splitting at the maximum. Adv. Appl. Prob. 12, 893–902.10.2307/1426747CrossRefGoogle Scholar
Itô, K. (1972). Poisson point processes attached to Markov processes. In Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 3: Probability Theory, pp. 225–239. University of California Press.Google Scholar
Kallenberg, O. (2002). Foundations of Modern Probability (Probability and Its Applications). Springer, New York.10.1007/978-1-4757-4015-8CrossRefGoogle Scholar
Kuznetsov, A., Kyprianou, A. E. and Rivero, V. (2013). The theory of scale functions for spectrally negative Lévy processes. In Lévy Matters II: Recent Progress in Theory and Applications: Fractional Lévy Fields, and Scale Functions, pp. 97–186. Springer, Berlin and Heidelberg.Google Scholar
Kyprianou, A. E. (2014). Fluctuations of Lévy Processes with Applications: Introductory Lectures. Springer, Berlin and Heidelberg.10.1007/978-3-642-37632-0CrossRefGoogle Scholar
Lamperti, J. W. (1972). Semi-stable Markov processes. Z. Wahrscheinlichkeitsth. 22, 205–225.10.1007/BF00536091CrossRefGoogle Scholar
Pardo, J. C., Patie, P. and Savov, M. (2012). A Wiener–Hopf type factorization for the exponential functional of Lévy processes. J. London Math. Soc. 86, 930–956.10.1112/jlms/jds028CrossRefGoogle Scholar
Patie, P. (2009). Infinite divisibility of solutions to some self-similar integro-differential equations and exponential functionals of Lévy processes. Ann. Inst. H. Poincaré Prob. Statist. 45, 667–684.Google Scholar
Patie, P. (2012). Law of the absorption time of some positive self-similar Markov processes. Ann. Prob. 40, 765–787.10.1214/10-AOP638CrossRefGoogle Scholar
Rivero, V. (2005). Recurrent extensions of self-similar Markov processes and Cramér’s condition. Bernoulli 11, 471–509.10.3150/bj/1120591185CrossRefGoogle Scholar
Rogers, L. C. G. (1984). A new identity for real Lévy processes. Ann. Inst. H. Poincaré Prob. Statist. 20, 21–34.Google Scholar
Sato, K. I. (1999). Lévy Processes and Infinitely Divisible Distributions (Cambridge Studies in Advanced Mathematics). Cambridge University Press.Google Scholar
Vidmar, M. (2019). First passage upwards for state-dependent-killed spectrally negative Lévy processes. J. Appl. Prob. 56, 472–495.10.1017/jpr.2019.23CrossRefGoogle Scholar