Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-18T20:12:18.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Tail behavior of negatively associated heavy-tailed sums

Part of: Distribution theory Stochastic processes

Published online by Cambridge University Press:  14 July 2016

Jaap Geluk  and
Kai W. Ng
Jaap Geluk*
Affiliation:
The Petroleum Institute, Abu Dhabi
Kai W. Ng*
Affiliation:
University of Hong Kong
*
∗Postal address: The Petroleum Institute, PO Box 2533, Abu Dhabi, United Arab Emirates. Email address: [email protected]
∗∗Postal address: Department of Statistics and Actuarial Science, University of Hong Kong, Pokfulam Road, Hong Kong. Email address: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

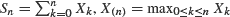Consider a sequence {Xk, k ≥ 1} of random variables on (−∞, ∞). Results on the asymptotic tail probabilities of the quantities , and S(n) = max0 ≤ k ≤ nSk, with X0 = 0 and n ≥ 1, are well known in the case where the random variables are independent with a heavy-tailed (subexponential) distribution. In this paper we investigate the validity of these results under more general assumptions. We consider extensions under the assumptions of having long-tailed distributions (the class L) and having the class D ∩ L, where D is the class of distribution functions with dominatedly varying tails. Some results are also given in the case where Xk, k ≥ 1, are not necessarily identically distributed and/or independent.

Keywords

Asymptoticssubexponentialitypartial sumtail probabilitynegative association

MSC classification

Primary: 60G50: Sums of independent random variables; random walks
Secondary: 62E20: Asymptotic distribution theory
Type
Short Communications
Information
Journal of Applied Probability , Volume 43 , Issue 2 , June 2006 , pp. 587 - 593
Copyright
© Applied Probability Trust 2006 

References

Alam, K. and Saxena, K. M. L. (1981). Positive dependence in multivariate distributions. Commun. Statist. A 10, 1183–1196.Google Scholar
Asmussen, S. (2000). Ruin Probabilities (Adv. Ser. Statist. Sci. Appl. Prob. 2). World Scientific, River Edge, NJ.Google Scholar
Asmussen, S., Kroese, D. P. and Rubinstein, R. Y. (2005). Heavy tails, importance sampling and cross-entropy. Stoch. Models 21, 57–76.Google Scholar
Bingham, N. H., Goldie, C. M. and Teugels, J. L. (1987). Regular Variation (Encyclopedia Math. Appl. 27). Cambridge University Press.Google Scholar
Boxma, O. J., Foss, S. G., Lasgouttes, J.-M. and Núñez Queija, R. (2004). Waiting time asymptotics in the single server queue with service in random order. Queueing Systems 46, 35–73.Google Scholar
Embrechts, P. and Goldie, C. M. (1980). On closure and factorization properties of subexponential and related distributions. J. Austral. Math. Soc. Ser. A 29, 243–256.Google Scholar
Embrechts, P., Goldie, C. M. and Veraverbeke, N. (1979). Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.CrossRefGoogle Scholar
Embrechts, P., Klüppelberg, C. and Mikosch, T. (1997). Modelling Extremal Events (Appl. Math. (New York) 33). Springer, Berlin.Google Scholar
Feller, W. (1971). An Introduction to Probability Theory and Its Applications, Vol. 2, 2nd edn. John Wiley, New York.Google Scholar
Geluk, J. (2004). Asymptotics in the symmetrization inequality. Statist. Prob. Lett. 69, 63–68.CrossRefGoogle Scholar
Geluk, J. L. and De Vries, C. G. (2006). Weighted sums of subexponential random variables and asymptotic dependence between returns on reinsurance equities. Insurance Math. Econom. 38, 39–56.Google Scholar
Joag-Dev, K. and Proschan, F. (1983). Negative association of random variables, with applications. Ann. Statist. 11, 286–295.Google Scholar
Ng, K. W. and Tang, Q. (2004). Asymptotic behavior of tail and local probabilities for sums of subexponential random variables. J. Appl. Prob. 41, 108–116.Google Scholar
Ng, K. W., Tang, Q. H. and Yang, H. (2002). Maxima of sums of heavy-tailed random variables. ASTIN Bull. 32, 43–55.CrossRefGoogle Scholar
Pakes, A. G. (2004). Convolution equivalence and infinite divisibility. J. Appl. Prob. 41, 407–424.Google Scholar
Peng, L. and Yao, Q. (2004). Nonparametric regression under dependent errors with infinite variance. Ann. Inst. Statist. Math. 56, 73–86.Google Scholar
Petrov, V. V. (1975). A generalization of an inequality of Lévy. Theory Prob. Appl. 20, 141–145.CrossRefGoogle Scholar
Rolski, T., Schmidli, H., Schmidt, V. and Teugels, J. (1999). Stochastic Processes for Insurance and Finance. John Wiley, Chichester.Google Scholar
Sgibnev, M. S. (1996). On the distribution of the maxima of partial sums. Statist. Prob. Lett. 28, 235–238.Google Scholar
Tang, Q. and Yan, J. (2002). A sharp inequality for the tail probabilities of sums of i.i.d. r.v.'s with dominatedly varying tails. Sci. China Ser. A 45, 1006–1011.Google Scholar
Wang, D. and Tang, Q. (2004). Maxima of sums and random sums for negatively associated random variables with heavy tails. Statist. Prob. Lett. 68, 287–295.CrossRefGoogle Scholar
Willekens, E. (1986). Hogere orde theorie voor subexponentiële verdelingen. , University of Leuven.Google Scholar
Zwart, B., Borst, S. and Mandjes, M. (2004). Exact asymptotics for fluid queues fed by multiple heavy-tailed on-off flows. Ann. Appl. Prob. 14, 903–957.CrossRefGoogle Scholar