Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-27T21:54:18.862Z Has data issue: false hasContentIssue false
  • English
  • Français

Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure

Part of: Stochastic processes Distribution theory - Probability Geometric probability and stochastic geometry

Published online by Cambridge University Press:  25 February 2021

Mads Stehr  and
Anders Rønn-Nielsen
Mads Stehr*
Affiliation:
Aarhus University
Anders Rønn-Nielsen*
Affiliation:
Copenhagen Business School
*
*Postal address: Centre for Stochastic Geometry and Advanced Bioimaging (CSGB), Department of Mathematics, Aarhus University, Ny Munkegade 118, 8000 Aarhus C, Denmark. Email address: [email protected]
**Postal address: Center for Statistics, Department of Finance, Copenhagen Business School, Solbjerg Pl. 3, 2000 Frederiksberg, Denmark.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a space-time random field on 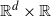${{\mathbb{R}^d} \times {\mathbb{R}}}$ given as an integral of a kernel function with respect to a Lévy basis with a convolution equivalent Lévy measure. The field obeys causality in time and is thereby not continuous along the time axis. For a large class of such random fields we study the tail behaviour of certain functionals of the field. It turns out that the tail is asymptotically equivalent to the right tail of the underlying Lévy measure. Particular examples are the asymptotic probability that there is a time point and a rotation of a spatial object with fixed radius, in which the field exceeds the level x, and that there is a time interval and a rotation of a spatial object with fixed radius, in which the average of the field exceeds the level x.

Keywords

Convolution equivalenceinfinite divisibilityLévy-based modellingasymptotic equivalencesample paths for random fields

MSC classification

Primary: 60G60: Random fields 60G17: Sample path properties
Secondary: 60E07: Infinitely divisible distributions; stable distributions 60D05: Geometric probability and stochastic geometry
Type
Research Papers
Information
Journal of Applied Probability , Volume 58 , Issue 1 , March 2021 , pp. 42 - 67
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The supplementary material for this article can be found at http://doi.org/10.1017/jpr.2020.73

References

Adler, R. J. (1981). The Geometry of Random Fields. John Wiley, New York.Google Scholar
Adler, R. J. and Taylor, J. E. (2007). Random Fields and Geometry. Springer, New York.Google Scholar
Adler, R. J., Samorodnitsky, G. and Taylor, J. E. (2010). Excursion sets of three classes of stable random fields. Adv. Appl. Prob. 42, 293–318.CrossRefGoogle Scholar
Adler, R. J., Samorodnitsky, G. and Taylor, J. E. (2013). High level excursion set geometry for non–Gaussian infinitely divisible random fields. Ann. Prob. 41, 134–169.CrossRefGoogle Scholar
Barndorff-Nielsen, O. E. and Schmiegel, J. (2004). Lévy-based tempo-spatial modelling with applications to turbulence. Uspekhi Mat. Nauk 159, 63–90.Google Scholar
Barndorff-Nielsen, O. E. and Shephard, N. (2001). Non-Gaussian Ornstein–Uhlenbeck-based models and some of their uses in financial economics. J. R. Statist. Soc. B 63, 167–241.CrossRefGoogle Scholar
Braverman, M. and Samorodnitsky, G. (1995). Functionals of infinitely divisible stochastic processes with exponential tails. Stoch. Process. Appl. 56, 207–231.CrossRefGoogle Scholar
Cline, D. B. H. (1986). Convolution tails, product tails and domains of attraction. Prob. Theory Relat. Fields 72, 529–557.CrossRefGoogle Scholar
Cline, D. B. H. (1987). Convolutions of distributions with exponential and subexponential tails. J. Austral. Math. Soc. 43, 347–365.CrossRefGoogle Scholar
Fasen, V. (2008). Extremes of Lévy driven mixed MA processes with convolution equivalent distributions. Extremes 12, 265–296.CrossRefGoogle Scholar
Hellmund, G., Prokešová, M. and Jensen, E. (2008). Lévy-based Cox point processes. Adv. Appl. Prob. 40, 603–629.CrossRefGoogle Scholar
Jónsdóttir, K. Y., Rønn-Nielsen, A., Mouridsen, K. and Jensen, E. B. V. (2013). Lévy-based modelling in brain imaging. Scand. J. Statist. 40, 511–529.CrossRefGoogle Scholar
Jónsdóttir, K. Y., Schmiegel, J. and Jensen, E. B. V. (2008). Lévy-based growth models. Bernoulli 14, 62–90.CrossRefGoogle Scholar
Kechris, A. (2012). Classical Descriptive Set Theory (Graduate Texts in Mathematics). Springer, New York.Google Scholar
Linde, W. (1983). Infinitely Divisible and Stable Measures on Banach Spaces (Teubner-Texte zur Mathematik). B.G. Teubner.Google Scholar
Pakes, A. G. (2004). Convolution equivalence and infinite divisibility. J. Appl. Prob. 41, 407–424.CrossRefGoogle Scholar
Peccati, G. and Taqqu, M. S. (2011). Combinatorial Expressions of Cumulants and Moments. Springer, Milan.CrossRefGoogle Scholar
Rajput, B. S. and Rosinski, J. (1989). Spectral representations of infinitely divisible processes. Prob. Theory Relat. Fields 82, 451–487.CrossRefGoogle Scholar
Rønn-Nielsen, A. and Jensen, E. B. V. (2016). Tail asymptotics for the supremum of an infinitely divisible field with convolution equivalent Lévy measure. J. Appl. Prob. 53, 244–261.CrossRefGoogle Scholar
Rønn-Nielsen, A. and Jensen, E. B. V. (2017). Excursion sets of infinitely divisible random fields with convolution equivalent Lévy measure. J. Appl. Prob. 54, 833–851.CrossRefGoogle Scholar
Rønn-Nielsen, A. and Jensen, E. B. V. (2019). Central limit theorem for mean and variogram estimators in Lévy-based models. J. Appl. Prob. 56, 209–222.CrossRefGoogle Scholar
Rønn-Nielsen, A., Sporring, J. and Jensen, E. B. V. (2017). Estimation of sample spacing in stochastic processes. Image Anal. Stereol. 36, 43–49.CrossRefGoogle Scholar
Rosinski, J. and Samorodnitsky, G. (1993). Distributions of subadditive functionals of sample paths of infinitely divisible processes. Ann. Prob. 21, 996–1014.CrossRefGoogle Scholar
Sato, K. (1999). Lévy Processes and Infinitely Divisible Distributions (Cambridge Studies in Advanced Mathematics). Cambridge University Press.Google Scholar
Sommerfeld, M., Sain, S. and Schwartzman, A. (2018). Confidence regions for spatial excursion sets from repeated random field observations, with an application to climate. J. Amer. Statist. Assoc. 113, 1327–1340.CrossRefGoogle ScholarPubMed
Spodarev, E. (2014). Limit theorems for excursion sets of stationary random fields. In Modern Stochastics and Applications, eds V. Korolyuk et al., pp. 221–241. Springer, Cham.CrossRefGoogle Scholar
Stehr, M. and Rønn-Nielsen, A. (2021). Tail asymptotics of an infinitely divisible space-time model with convolution equivalent Lévy measure: supplementary material. Available at http://doi.org/10.1017/jpr.2020.73.CrossRefGoogle Scholar
Supplementary material: PDF

Stehr and Rønn-Nielsen supplementary material

Stehr and Rønn-Nielsen supplementary material 1
Download Stehr and Rønn-Nielsen supplementary material(PDF)
PDF 317.7 KB
Supplementary material: File

Stehr and Rønn-Nielsen supplementary material

Stehr and Rønn-Nielsen supplementary material 2

Download Stehr and Rønn-Nielsen supplementary material(File)
File 30.2 KB