Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-28T17:51:15.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Surprising identities for the greedy independent set on Cayley trees

Part of: Graph theory Algorithms - Computer Science Markov processes

Published online by Cambridge University Press:  25 August 2022

Alice Contat
Alice Contat*
Affiliation:
Université Paris-Saclay
*
*Postal address: Institut Mathématiques d’Orsay, Bâtiment 307, Université Paris-Saclay, 91405 Orsay, France. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a surprising symmetry between the law of the size 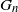$G_n$ of the greedy independent set on a uniform Cayley tree 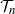$ \mathcal{T}_n$ of size n and that of its complement. We show that 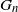$G_n$ has the same law as the number of vertices at even height in 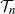$ \mathcal{T}_n$ rooted at a uniform vertex. This enables us to compute the exact law of 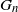$G_n$ . We also give a Markovian construction of the greedy independent set, which highlights the symmetry of 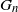$G_n$ and whose proof uses a new Markovian exploration of rooted Cayley trees that is of independent interest.

Keywords

Cayley treesindependent setgreedy

MSC classification

Primary: 05C80: Random graphs
Secondary: 68W20: Randomized algorithms 60J10: Markov chains (discrete-time Markov processes on discrete state spaces)
Type
Original Article
Information
Journal of Applied Probability , Volume 59 , Issue 4 , December 2022 , pp. 1042 - 1058
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aldous, D. J. (1990). The random walk construction of uniform spanning trees and uniform labelled trees. SIAM J. Discrete Math. 3, 450–465.CrossRefGoogle Scholar
Aldous, D. (1991). The continuum random tree I. Ann. Prob. 19, 1–28.CrossRefGoogle Scholar
Aldous, D. (1993). The continuum random tree III. Ann. Prob. 21, 248–289.CrossRefGoogle Scholar
Aldous, D. and Steele, J. M. (2004). The objective method: probabilistic combinatorial optimization and local weak convergence. In Probability on Discrete Structures (Encyclopaedia Math. Sci. 110), pp. 1–72. Springer, Berlin.CrossRefGoogle Scholar
Bermolen, P., Jonckheere, M. and Moyal, P. (2017). The jamming constant of uniform random graphs. Stoch. Process. Appl. 127, 2138–2178.CrossRefGoogle Scholar
Brightwell, G., Janson, S. and Luczak, M. (2017). The greedy independent set in a random graph with given degrees. Random Structures Algorithms 51, 565–586.CrossRefGoogle Scholar
Broder, A. Z. (1989). Generating random spanning trees. In 30th Annual Symposium on Foundations of Computer Science (FOCS 1989), pp. 442–447. IEEE.CrossRefGoogle Scholar
Camarri, M. and Pitman, J. (2000). Limit distributions and random trees derived from the birthday problem with unequal probabilities. Electron. J. Prob. 5, 1–18.CrossRefGoogle Scholar
Chaumont, L. and Liu, R. (2016). Coding multitype forests: application to the law of the total population of branching forests. Trans. Amer. Math. Soc. 368, 2723–2747.CrossRefGoogle Scholar
Contat, A. and Curien, N. (2021). Parking on Cayley trees & frozen Erdős–Rényi. Available at arXiv:2107.02116.Google Scholar
Curien, N. (2019). Peeling Random Planar Maps: Saint-Flour Course 2019. Available at https://www.imo.universite-paris-saclay.fr/~curien/ Google Scholar
Dyer, M., Frieze, A. and Pittel, B. (1993). The average performance of the greedy matching algorithm. Ann. Appl. Prob. 3, 526–552.CrossRefGoogle Scholar
Ethier, S. N. and Kurtz, T. G. (2009). Markov Processes: Characterization and Convergence (Wiley Series in Probability and Statistics). John Wiley.Google Scholar
Féray, V. and Kortchemski, I. (2018). The geometry of random minimal factorizations of a long cycle via biconditioned bitype random trees. Ann. Henri Lebesgue 1, 149–226.CrossRefGoogle Scholar
Frieze, A. and McDiarmid, C. (1997). Algorithmic theory of random graphs. Random Structures Algorithms 10, 5–42.3.0.CO;2-Z>CrossRefGoogle Scholar
Haas, B. and Miermont, G. (2012). Scaling limits of Markov branching trees, with applications to Galton–Watson and random unordered trees. Ann. Prob. 40, 2589–2666.CrossRefGoogle Scholar
Jonckheere, M. and Sáenz, M. (2021). Asymptotic optimality of degree-greedy discovering of independent sets in configuration model graphs. Stoch. Process. Appl. 131, 122–150.CrossRefGoogle Scholar
Krivelevich, M., Mészáros, T., Michaeli, P. and Shikhelman, C. (2020). Greedy maximal independent sets via local limits. In 31st International Conference on Probabilistic, Combinatorial and Asymptotic Methods for the Analysis of Algorithms (AofA 2020), art. 20. Dagstuhl Publishing.Google Scholar
Le Gall, J.-F. (2005). Random trees and applications. Prob. Surv. 2, 245–311.CrossRefGoogle Scholar
Meir, A. and Moon, J. W. (1973). The expected node-independence number of random trees. Indag. Math. 76, 335–341.CrossRefGoogle Scholar
Panholzer, A. (2020). A combinatorial approach for discrete car parking on random labelled trees. J. Combinatorial Theory A 173, 105233.CrossRefGoogle Scholar
Pitman, J. (1999). Coalescent random forests. J. Combinatorial Theory A 85, 165–193.CrossRefGoogle Scholar