Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T06:27:55.576Z Has data issue: false hasContentIssue false
  • English
  • Français

Supercritical age-dependent branching processes with immigration

Published online by Cambridge University Press:  14 July 2016

K. B. Athreya ,
P. R. Parthasarathy  and
G. Sankaranarayanan
K. B. Athreya
Affiliation:
Indian Institute of Science, Bangalore
P. R. Parthasarathy
Affiliation:
Annamalai University, Annamalai Nagar
G. Sankaranarayanan
Affiliation:
Annamalai University, Annamalai Nagar
Get access Rights & Permissions [Opens in a new window]

Abstract

A branching process with immigration of the following type is considered. For every i, a random number Ni of particles join the system at time 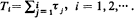. These particles evolve according to a one-dimensional age-dependent branching process with offspring p.g.f. 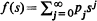and life time distribution G(t). Assume 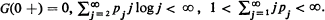. Then it is shown that Z(t) e–αt converges in distribution to an extended real-valued random variable Y where a is the Malthusian parameter. We do not require the sequences {τi} or {Ni} to be independent or identically distributed or even mutually independent.

Keywords

SUPERCRITICALIMMIGRATIONAGE-DEPENDENTBRANCHING PROCESSESMALTHUSIAN PARAMETERCONVERGENCE IN DISTRIBUTION
Type
Research Papers
Information
Journal of Applied Probability , Volume 11 , Issue 4 , December 1974 , pp. 695 - 702
Copyright
Copyright © Applied Probability Trust 1974 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Athreya, K. B. (1969) On the super-critical one-dimensional age-dependent branching processes. Ann. Math. Statist. 40, 743–763.Google Scholar
[2]Athreya, K. B. and Ney, P. E. (1972) Branching Processes. Springer Verlag, Berlin.Google Scholar
[3]Doney, R. A. (1971) The total progeny of branching processes. J. Appl. Prob. 8, 407–412.Google Scholar
[4]Levinson, N. (1960) Limiting theorems for age-dependent branching processes. Ill. J. Math. 4, 100–118.Google Scholar
[5]Parthasarathy, P. R. Age-dependent branching processes with random immigration. Submitted for publication.Google Scholar
[6]Sankaranarayanan, G. and Parthasarathy, P. R. (1972) Age-dependent branching processes, with immigration. Proceedings of the Indian Census Centenary Seminar, 1972.Google Scholar
[7]Seneta, E. (1970) On the super-critical Galton-Watson processes with immigration. Math. Biosci. 7, 9–14.Google Scholar