Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-28T20:03:41.342Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure functions with finite minimal vector sets

Published online by Cambridge University Press:  14 July 2016

Laurence A. Baxter  and
Seung Min Lee
Laurence A. Baxter*
Affiliation:
State University of New York at Stony Brook
Seung Min Lee*
Affiliation:
State University of New York at Stony Brook
*
∗Postal address: Department of Applied Mathematics and Statistics, State University of New York at Stony Brook, Stony Brook, NY 11794, USA.
∗∗Present address: Department of Statistics, Hallym University, 1 Okchon-dong, Chunchon 200, Korea.
Get access Rights & Permissions [Opens in a new window]

Abstract

A continuum structure function (CSF) y is a non-decreasing mapping from the unit hypercube to the unit interval. Define 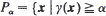whereas γ (γ) < α for all y < x}, the set of minimal vectors to level α. This paper examines CSFs for which each Pα is finite. It is shown that if γ is such a CSF and X is a vector of independent random variables, the distribution of γ (X) is readily calculated. Further, if γ is an arbitrary right-continuous CSF, the distribution of γ (X) may be approximated arbitrarily closely by that of γ′(X) where γ′ is a right-continuous CSF for which each minimal vector set is finite.

Keywords

CONTINUUM STRUCTURE FUNCTIONMINIMAL VECTOR SETREDUCTION MAPPINGSTOCHASTIC PERFORMANCE FUNCTION
Type
Short Communications
Information
Journal of Applied Probability , Volume 26 , Issue 1 , March 1989 , pp. 196 - 201
Copyright
Copyright © Applied Probability Trust 1989 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Research supported by the Air Force Office of Scientific Research, AFSC, USAF under grant AFOSR-86-0136. The US Government is authorised to reproduce and distribute reprints for Governmental purposes notwithstanding any copyright notation thereon.

References

Baxter, L. A. (1984) Continuum structures I. J. Appl. Prob. 21, 802–815.CrossRefGoogle Scholar
Baxter, L. A. (1986) Continuum structures II. Math. Proc. Camb. Phil. Soc. 99, 331–338.CrossRefGoogle Scholar
Baxter, L. A. and Kim, C. (1986) Bounding the stochastic performance of continuum structure functions I. J. Appl. Prob. 23, 660–669.CrossRefGoogle Scholar
Baxter, L. A. and Kim, C. (1987) Bounding the stochastic performance of continuum structure functions II. J. Appl. Prob. 24, 609–618.CrossRefGoogle Scholar
Block, H. W. and Savits, T. H. (1984) Continuous multistate structure functions. Operat. Res. 32, 703–714.CrossRefGoogle Scholar
Griffith, W. S. (1980) Multistate reliability models. J. Appl. Prob. 17, 735–744.CrossRefGoogle Scholar
Natvig, B., Sørmo, S., Holen, A. T. and Høgåsen, G. (1986) Multistate reliability theory — a case study. Adv. Appl. Prob. 18, 921–932.CrossRefGoogle Scholar