Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-08T21:35:10.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic properties of generalized finite mixture models with dependent components

Part of: Operations research and management science Special processes Distribution theory - Probability

Published online by Cambridge University Press:  16 September 2021

Ebrahim Amini-Seresht  and
Narayanaswamy Balakrishnan
Ebrahim Amini-Seresht*
Affiliation:
Bu-Ali Sina University
Narayanaswamy Balakrishnan*
Affiliation:
McMaster University
*
*Postal address: Department of Statistics, Bu-Ali Sina University, Hamedan, Iran. Email address: [email protected]
**Department of Mathematics and Statistics, McMaster University, Hamilton, Ontario, Canada. Email address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider a new generalized finite mixture model formed by dependent and identically distributed (d.i.d.) components. We then establish results for the comparisons of lifetimes of two such generalized finite mixture models in two different cases: (i) when the two mixture models are formed from two random vectors 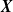$\textbf{X}$ and 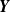$\textbf{Y}$ but with the same weights, and (ii) when the two mixture models are formed with the same random vectors but with different weights. Because the lifetimes of k-out-of-n systems and coherent systems are special cases of the mixture model considered, we used the established results to compare the lifetimes of k-out-of-n systems and coherent systems with respect to the reversed hazard rate and hazard rate orderings.

Keywords

Coherent systemk-out-of-n systemstochastic ordergeneralized mixture modelcopula function

MSC classification

Primary: 90B25: Reliability, availability, maintenance, inspection
Secondary: 60E15: Inequalities; stochastic orderings 60K10: Applications (reliability, demand theory, etc.)
Type
Original Article
Information
Journal of Applied Probability , Volume 58 , Issue 3 , September 2021 , pp. 794 - 804
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Amini-Seresht, E. and Khaledi, B.-E. (2015). Multivariate stochastic comparisons of mixture models. Metrika 78, 1015–1034.CrossRefGoogle Scholar
Amini-Seresht, E. and Zhang, Y. (2017). Stochastic comparisons on two finite mixture models. Operat. Res. Lett. 45, 475–480.CrossRefGoogle Scholar
Amini-Seresht, E., Zhang, Y. and Balakrishnan, N. (2018). Stochastic comparisons of coherent systems under different random environments. J. Appl. Prob. 55, 459–472.CrossRefGoogle Scholar
Belzunce, F., Mercader, J.-A., Ruiz, J.-M. and Spizzichino, F. (2009). Stochastic comparisons of multivariate mixture models. J. Multivariate Anal. 100, 1657–1669.CrossRefGoogle Scholar
Gupta, R. C. (2002). Reliability of a k out of n system of components sharing a common environment. Appl. Math. Lett. 15, 837–844.CrossRefGoogle Scholar
Gupta, R. C. and Gupta, R. D. (2009). General frailty model and stochastic orderings. J. Statist. Planning Infer. 139, 3277–3287.CrossRefGoogle Scholar
Gupta, N., Dhariyal, I. D. and Misra, N. (2011). Reliability under random operating environment: frailty models. J. Combin. Inform. System Sci. 35, 117–133.Google Scholar
Khaledi, B.-E. and Shaked, M. (2010). Stochastic comparisons of multivariate mixtures. J. Multivariate Anal. 101, 2486–2498.CrossRefGoogle Scholar
Kuo, W. and Zuo, M. J. (2003). Optimal Reliability Modeling: Principles and Applications. John Wiley, New York.Google Scholar
Li, X. and Da, G. (2010). Stochastic comparisons in multivariate mixed model of proportional reversed hazard rate with application. J. Multivariate Anal. 101, 1016–1025.CrossRefGoogle Scholar
Li, X. and Zhao, P. (2011). On the mixture of proportional odds models. Commun. Statist. Theory Meth. 40, 333–344.CrossRefGoogle Scholar
Misra, N., Gupta, N. and Gupta, R. D. (2009). Stochastic comparisons of multivariate frailty models. J. Statist. Planning Infer. 139, 2084–2090.CrossRefGoogle Scholar
MÜller, A. and Stoyan, D. (2002). Comparison Methods for Stochastic Models and Risks. John Wiley, New York.Google Scholar
Navarro, J. (2016). Stochastic comparisons of generalized mixtures and coherent systems. TEST 25, 150–169.CrossRefGoogle Scholar
Navarro, J., del Águila, Y., Sordo, M. A. and Suárez-Llorens, A. (2013). Stochastic ordering properties for systems with dependent identically distributed components. Appl. Stoch. Models Business Industry 29, 264–278.CrossRefGoogle Scholar
Navarro, J., del Águila, Y., Sordo, M. A. and Suárez-Llorens, A. (2016). Preservation of stochastic orders under the formation of generalized distorted distributions: applications to coherent systems. Methodology Comput. Appl. Prob. 18, 529–545.10.1007/s11009-015-9441-zCrossRefGoogle Scholar
Navarro, J., Guillamón, A. and Ruiz, M. C. (2009). Generalized mixtures in reliability modelling: applications to the construction of bathtub shaped hazard models and the study of systems. Appl. Stoch. Models Business Industry 25, 323–337.CrossRefGoogle Scholar
Nelsen, R. B. (2006). An Introduction to Copulas. Springer, New York.Google Scholar
Samaniego, F. J. (1985). On closure of the IFR class under formation of coherent systems. IEEE Trans. Reliab. 34, 69–72.CrossRefGoogle Scholar
Samaniego, F. J. and Navarro, J. (2016). On comparing coherent systems with heterogeneous components. J. Appl. Prob. 48, 88–111.10.1017/apr.2015.8CrossRefGoogle Scholar
Shaked, M. and Shanthikumar, J. G. (2007). Stochastic Orders. Springer, New York.CrossRefGoogle Scholar