Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-17T01:10:00.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic formation of hierarchies

Published online by Cambridge University Press:  14 July 2016

L. L. Helms
L. L. Helms*
Affiliation:
University of Illinois, Urbana-Champaign
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, N particles el, · ··, eN occupying positions in finite state spaces S1, · ··, SN, respectively, are considered along with an element of a finite space S N+1 of hierarchies which describe the organization of the particles into pairs, pairs of pairs, etc. A stochastic process {Xt: t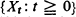 0} on a probability measure space (Ω, 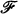, P) is a hierarchic process if it is a right-continuous Markov jump process taking on values in the state space 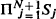Sj and having the property that the (N + 1)th component of Xt can jump from a hierarchy to a successor or antecedent of that hierarchy. Asymptotic distributions of perturbed hierarchic processes, bilateral processes, and unilateral processes are determined in terms of an interaction function and the asymptotic distributions of the particles in the absence of any interaction.

Keywords

HIERARCHIESHIERARCHIC PROCESSESSPEED FUNCTIONSINTERACTING PARTICLESASYMPTOTIC DISTRIBUTIONERGODIC THEORYMARKOV PROCESSES
Type
Research Papers
Information
Journal of Applied Probability , Volume 10 , Issue 1 , March 1973 , pp. 27 - 38
Copyright
Copyright © Applied Probability Trust 1973 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Doob, J. L. (1953) Stochastic Processes. Wiley, New York.Google Scholar
[2] Dynkin, E. B. (1965) Markov Processes. Vol. I. Springer-Verlag, Berlin.Google Scholar
[3] Spitzer, F. (1970) Interaction of Markov processes. Advances in Math. 5, 246–290.CrossRefGoogle Scholar
[4] Volkonskii, V. A. (1958) Random substitution of time in strong Markov processes. Theor. Probability Appl. 3, 310–325.CrossRefGoogle Scholar