Article contents
Stochastic comparisons of order statistics under multivariate imperfect repair
Published online by Cambridge University Press: 14 July 2016
Abstract
A monotone coupling of order statistics from two sets of independent non-negative random variables Xi, i = 1, ···, n, and Yi, i = 1, ···, n, means that there exist random variables X′i, Y′i, i = 1, ···, n, on a common probability space such that 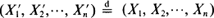 ,
, 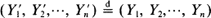 and
and 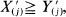 a.s. j = 1, ···, n, where X(1) ≦ X(2) ≦ ·· ·≦ X(n) are the order statistics of Xi, i = 1, ···, n (with the corresponding notations for the X′, Y, Y′ sample). In this paper, we study the monotone coupling of order statistics of lifetimes in two multi-unit systems under multivariate imperfect repair. Similar results for a special model due to Ross are also given.
a.s. j = 1, ···, n, where X(1) ≦ X(2) ≦ ·· ·≦ X(n) are the order statistics of Xi, i = 1, ···, n (with the corresponding notations for the X′, Y, Y′ sample). In this paper, we study the monotone coupling of order statistics of lifetimes in two multi-unit systems under multivariate imperfect repair. Similar results for a special model due to Ross are also given.
MSC classification
- Type
- Research Papers
- Information
- Copyright
- Copyright © Applied Probability Trust 1996
Footnotes
Research supported by a NNSF of China and a grant of Chinese Academy of Sciences.
References
- 5
- Cited by


