Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T07:03:34.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Stationary M/G/1 excursions in the presence of heavy tails

Part of: Stochastic processes Special processes

Published online by Cambridge University Press:  14 July 2016

Søren Asmussen  and
Claudia Klüppelberg
Søren Asmussen*
Affiliation:
University of Lund
Claudia Klüppelberg*
Affiliation:
Johannes Gutenberg University
*
∗Postal address: Department of Mathematical Statistics, University of Lund, Box 118, S-221 00 Lund, Sweden.
∗∗Postal address: Department of Mathematics, Johannes Gutenberg University, D-55099 Mainz, Germany.
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that the stationary excursions above level x for the stationary M/G/1 queue with the service time distribution belonging to a certain class 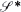of subexponential distributions are asymptotically of two types as x →∞: either the excursion starts with a jump from a level which is O(1) and the initial excess over x converges to ∞, or it starts from a level of the form x – O(1) and the excess has a proper limit distribution. The two types occur with probabilities ρ, resp. 1 – ρ.

Keywords

EXCURSIONOVERSHOOTQUEUEING THEORYREGULAR VARIATIONPALM THEORYSPATIALLY HOMOGENEOUS PROCESSSUBEXPONENTIAL DISTRIBUTION

MSC classification

Primary: 60G17: Sample path properties 60K25: Queueing theory
Type
Research Papers
Information
Journal of Applied Probability , Volume 34 , Issue 1 , March 1997 , pp. 208 - 212
Copyright
Copyright © Applied Probability Trust 1997 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Abate, J., Choudhury, G. L. and Whitt, W. (1995) Exponential approximations for tail probabilities of queues. Operat. Res. 73, 885–901.Google Scholar
[2] Abate, J., Choudhury, G. L. and Whitt, W. (1994) Asymptotics for steady-state tail probabilities in structured Markov queueing models. Stoch. Models 10, 99–173.Google Scholar
[3] Embrechts, P., Goldie, C. M. and Veraverbeke, N. (1979) Subexponentiality and infinite divisibility. Z. Wahrscheinlichkeitsth. 49, 335–347.Google Scholar
[4] Embrechts, P. and Veraverbeke, N. (1982) Estimates for the probability of ruin with special emphasis on the possibility of large claims. Insurance: Math. Econ. 1, 55–72.Google Scholar
[5] Guillemin, F. M. and Mazumdar, R. R. (1995) Excursions of the workload process in G/GI/1 queues. Stoch. Proc. Appl. (to appear).Google Scholar
[6] Klüppelberg, C. (1988) Subexponential distributions and exponential tails. J. Appl. Prob. 25, 132–141.Google Scholar
[7] Klüppelberg, C. (1989) Subexponential distributions and characterizations of related classes. Prob. Theory Rel. Fields 82, 259–269.Google Scholar
[8] Klüppelberg, C. (1989) Estimation of ruin probabilities by means of hazard rates. Insurance: Math. Econ. 8, 279–285.Google Scholar
[9] Neuts, M. F. (1988) Profile curves for the M/G/1 queue with group arrivals. Stoch. Models 4, 277–298.Google Scholar
[10] Neuts, M. F. (1995) Personal communication.Google Scholar
[11] Pitman, J. W. (1995) Stationary excursions. Seminaire de Probabilites XII. (Lecture Notes in Mathematics 1247.) Springer, Berlin. pp 289–302.Google Scholar
[12] Sigman, K. (1994) Stationary Marked Point Processes: An Intuitive Approach. Chapman and Hall, New York.Google Scholar
[13] Wolff, R. W. (1990) Stochastic Modeling and the Theory of Queues. Prentice-Hall, New York.Google Scholar