Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Krone, Stephen M.
and
Neuhauser, Claudia
2000.
A spatial model of range-dependent succession.
Journal of Applied Probability,
Vol. 37,
Issue. 04,
p.
1044.
Krone, Stephen M.
and
Neuhauser, Claudia
2000.
A spatial model of range-dependent succession.
Journal of Applied Probability,
Vol. 37,
Issue. 4,
p.
1044.
Sega, Gregor
2009.
Large-range constant threshold growth model in one dimension.
Electronic Journal of Probability,
Vol. 14,
Issue. none,


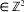 , once infected, remains so for a period of time
, once infected, remains so for a period of time 